城市通电(prim算法)
acwing3728 蓝桥杯集训每日一题
平面上遍布着 n 座城市,编号 1∼n。
第 i 座城市的位置坐标为 (xi,yi)
不同城市的位置有可能重合。
现在要通过建立发电站和搭建电线的方式给每座城市都通电。
一个城市如果建有发电站,或者通过电线直接或间接的与建有发电站的城市保持连通,则该城市通电。
在城市 i 建立发电站的花费为 ci 元。
在城市 i 与城市 j 之间搭建电线所需的花费为每单位长度 ki+kj 元。
电线只能沿上下左右四个方向延伸,电线之间可以相互交叉,电线都是双向的。
每根电线都是由某个城市沿最短路线搭建到另一个城市。
也就是说,如果在城市 i 与城市 j 之间搭建电线,则电线的长度为 |xi−xj|+|yi−yj|。
请问,如何合理设计通电方案,可以使得所有城市都成功通电,且花费最少?
输出最少花费和具体方案。
如果方案不唯一,则输出任意一种合理方案均可。
输入格式
第一行包含整数 n。
接下来 n 行,其中第 i 行包含两个整数 xi,yi,用来描述城市 i 的横纵坐标。
再一行包含 n 个整数 c1,c2,…,cn,用来描述每个城市建立发电站的花费。
最后一行包含 n 个整数 k1,k2,…,kn。
输出格式
第一行输出所需要的最少花费。
第二行输出一个整数 v,表示需要建立发电站的数量。
第三行输出 v 个整数,表示建立发电站的城市编号,注意输出编号要在范围 [1,n]内。且输出编号不应重复。输出编号顺序随意。
第四行输出一个整数 e,表示需要搭建的电线数量。
接下来 e 行,每行输出两个整数 a,b,表示要在城市 a 和 b 之间搭建电线。注意,任意两个城市之间最多只需要搭建一根电线,也就是说,对于每个 (a,b),不要有多余的 (a,b) 或 (b,a) 输出。a 和 b 不能相同,且要在范围 [1,n]内。输出电线顺序随意。
如果答案不唯一,输出任意合理方案即可。
数据范围
对于前三个测试点,1≤n≤3。
对于全部测试点,1≤n≤2000,1≤xi,yi≤10^6,1≤ci,ki≤10^9。
输入样例1:
3
2 3
1 1
3 2
3 2 3
3 2 3
输出样例1:
8
3
1 2 3
0
输入样例2:
3
2 1
1 2
3 3
23 2 23
3 2 3
输出样例2:
27
1
2
2
1 2
2 3
| 难度:困难 |
| 时/空限制:2s / 256MB |
| 总通过数:594 |
| 总尝试数:1351 |
| 来源:AcWing,第5场周赛 |
| 算法标签 最小生成树Prim |
考虑到最小生成树的prim算法
本题要将所有城市连接起来,两种方式,一是直接连接发电站,花费为c[i],二是连接一个城市,该城市已经直接连接或者间接连接发电站。
ans1数组存建立发电站的城市序号,ans2存连接在两城市之间的电路
考虑用pair形式存储该点连接的城市还是发电站 以及 花费
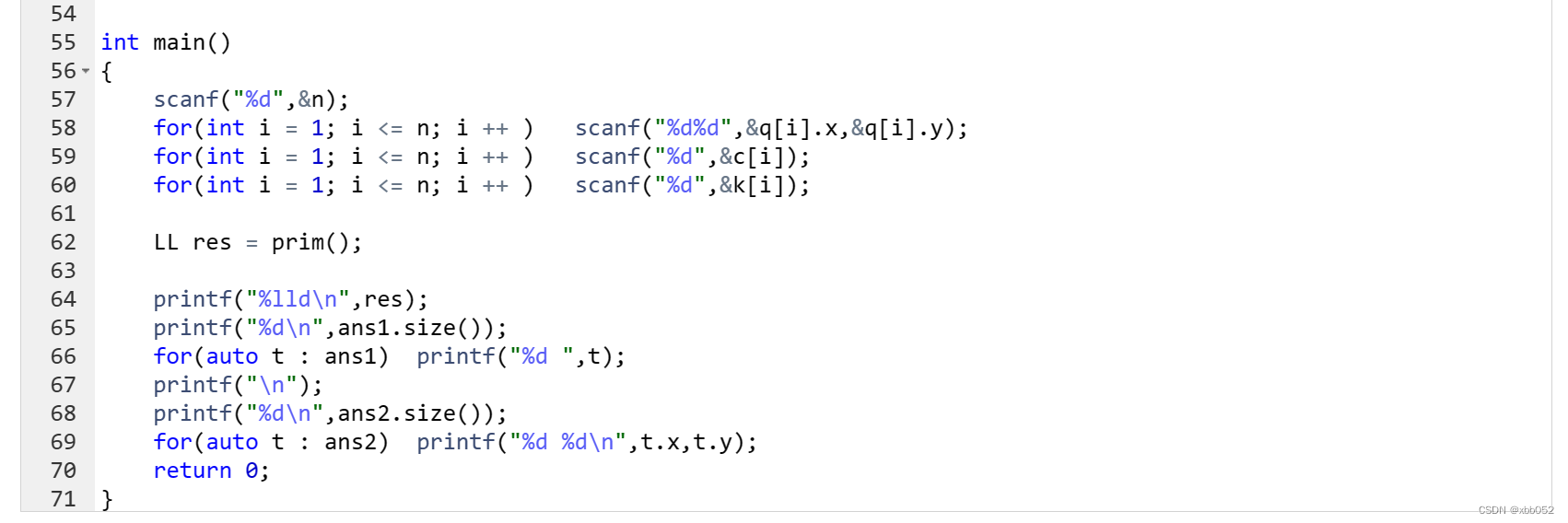
代码详解如下:

prim算法: 前面为初始化,表示一个超级原点,并初始化所有dist[i] 为直接在该城市建立发电站的花费c[i]。 接下来迭代n次,找到距离最近并且不在集合内的点,放入集合,最后用该点更新其他所有的点