Learning Feature Sparse Principal Subspace 论文阅读
1 Abstract:
- 这篇论文提出了新的算法来解决特征稀疏约束的主成分分析问题(FSPCA),该问题同时执行特征选择和PCA。现有的FSPCA优化方法需要对数据分布做出假设,并且缺乏全局收敛性的保证。尽管一般的FSPCA问题是NP难问题,我们展示了对于低秩协方差,FSPCA可以全局解决(算法1)。然后,我们提出了另一种策略(算法2),通过迭代构建一个精心设计的代理来解决一般协方差情况下的FSPCA问题,并保证收敛性。我们为新算法提供了(数据依赖的)近似界限和收敛性保证。对于具有指数/Zipf分布的协方差谱,我们提供了指数/多项式近似界限。实验结果表明,与最先进的方法相比,新算法在合成数据和真实世界数据集上表现出有希望的性能和效率。
2 Object function:

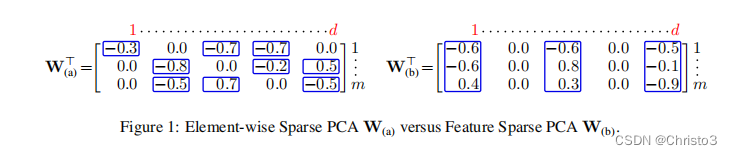
3 Solving strategy:


4 Summarize
-
算法原理可以分为两部分:
低秩协方差矩阵的全局最优解(Algorithm 1):
当协方差矩阵A的秩小于或等于m时,算法可以找到一个全局最优解。这是因为在低秩情况下,可以直接通过选择A中最大的k个特征值对应的特征向量来构建W,从而得到一个最优的稀疏主子空间。
算法首先确定A中最大的k个特征值,并选择对应的特征向量。这些特征向量构成了一个矩阵V,然后通过V与一个选择矩阵S相乘得到最终的W,其中S是根据特征值的大小选择特定行的矩阵。高秩协方差矩阵的迭代代理更新(Algorithm 2):
对于高秩协方差矩阵A,算法采用迭代方法来近似解决FSPCA问题。算法构建一个低秩代理矩阵P,然后用这个P来近似原始问题。
在每次迭代中,算法首先使用当前估计的W来构建代理矩阵Pt。这个代理矩阵Pt是通过AWt(WtAWt)†WtA(其中Wt是当前迭代的W)来计算的,它是一个低秩矩阵,其秩不超过m。
然后,算法使用Algorithm 1来解决代理矩阵Pt的FSPCA问题,得到新的Wt+1。
这个迭代过程继续进行,直到Wt+1与Wt相等,即算法收敛。
论文还提供了对这两个算法的理论分析,包括近似界和收敛保证。特别是,对于具有指数或Zipf分布的协方差矩阵谱,论文提供了相应的近似界。
