算法刷题应用知识补充--基础算法、数据结构篇
这里写目录标题
- 枚举
- 结
- 排序
- 结
- 模拟
- 结
- 二分
- 题
- 结
- 高精度
- 加、乘
- 题
- 结
- 减
- 题
- 结
- 除
- 题
- 结
- 结
- 位运算(均是拷贝运算,不会影响原数据,这点要注意)
- &、|、^
- 位运算特性+细节
- 知识补充
- 对于n-1的理解
- 异或来实现数字交换
- 找到只出现一次的数据,其余数据出现偶数次
- >> 、<<
- 二进制中相邻的位的特点
- 找出某个排列的所有子集
- 栈
- 题
- 结
- 单链表
- 题
- 结
- 双链表
- 题
- 结
- 队列
- 二级目录
- 二级目录
- 哈希表
- 题
- 结
- 字符串哈希
- 题
- 结
枚举
结
此类题就是暴力解法即可,大部分需要枚举题目范围的所有情况
排序
结
使用算法sort即可
模拟
结
题目说啥,我们做啥,就按照题目描述来
二分
题

结
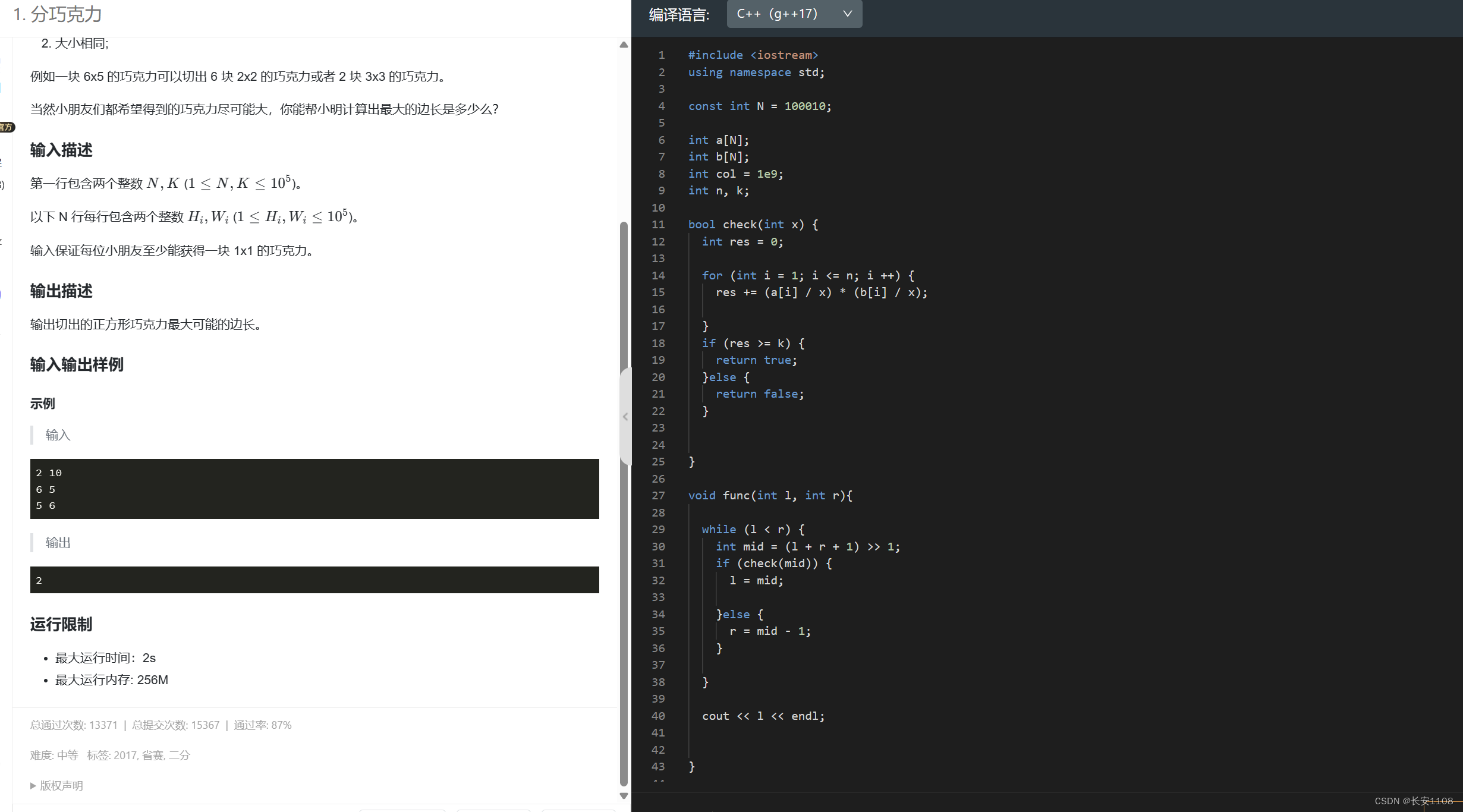
二分,就是对于一组单调的数据,两边的性质不同,二分可以找到某一边性质的最值,
如果找红色区间,则会找到满足红色性质的最大值(如果是红色区间,mid =( l + r + 1) >> 1)
如果找绿色区间,则会找到满足绿色性质的最小值(绿色区间则正常,mid = (l + r) >> 1)
补充:如果出错了,考虑check函数是否写错,是否疏忽了一些情况,比如此题,题目并没有说所有的巧克力原料都要用,所以,直接判断遍历所有的边长,如果有些边长比x小,则算出来是0,表示不使用该巧克力
注意点:最后 L == R 跳出循环,注意,最后有用的不是在循环中定义的那个mid,而是L R 或者num[L] num[R]
高精度
加、乘
题


结
二者的核心思想都是根据遍历,将当前位的运算都加到 t 身上,之后push(t % 10),然后更新 t = t / 10(这一步很精妙,表示如果 t
小于10,那么就不用进位,如果不是,那么就拿出其十位,加到 t ,为下一位的计算储备材料)
不同的是:加法最后如果 t 不为0,则补1,乘法则补 t
减
题

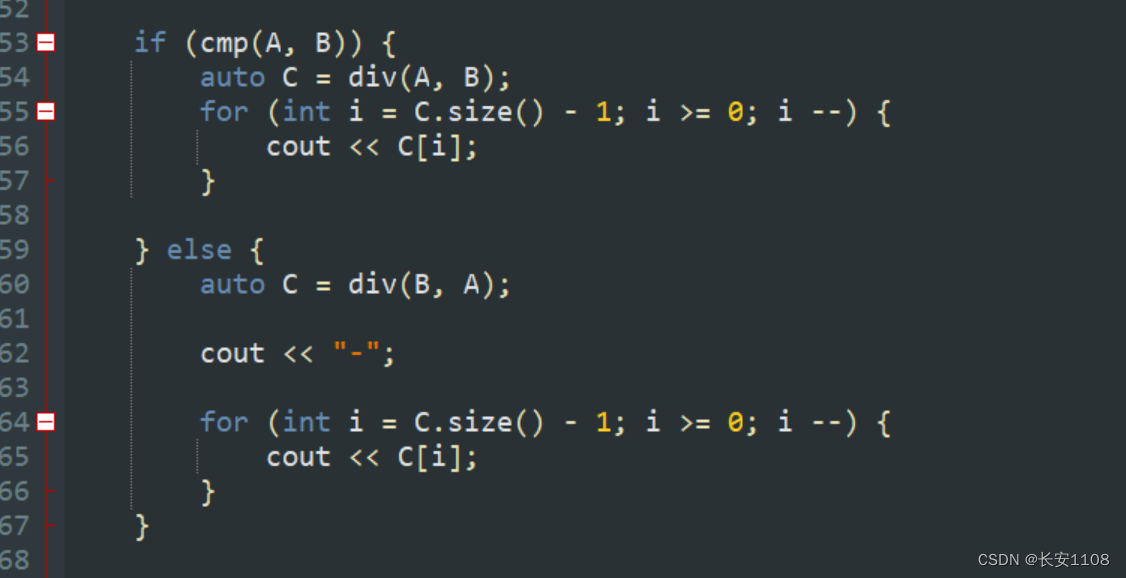
减法要先进行A 和 B的大小判断,看是A大还是B大,我们统一假设A大,也就是A大的话返回true,所以才会有上面的函数,且最后如果if和for都没有返回的话,最后返回true,表示A==B,所以相等的情况我们也是返回true,所以,该函数是判断是否A>=B
将大的传入div函数:(且如果题目规定求A-B,但是我们判断出B比A大,那么我们还是将B、A传入,最后输出的时候输出负号即可)
结
该题目也是,每次根据情况,将当前位的数 全部给到 t ,之后压入直接压t小于0的情况:(t + 10)% 10
之后判断t是不是真的小于0,如果是,那么 t 赋值为1,如果不是,那么 t 拨乱反正,改回0
最后要去除前导0
除
题

除法有三个参数,第三个参数是余数,且是引用,说明可以通过引用来返回余数是多少
且除法与其他不同,其他的函数内都是从0开始,这里是从后面开始,因为存入时,数据的高位在后面,除法要从高位开始
之后,是将所有的当前的数据加到 r 身上,然后push(r / b),且更新 r = r % b(更新余数)
最后要将其倒序,要将数据的高位放到容器末尾,这样方便去除前导0

传入时,由于第三个参数是传出参数,所以直接传入一个int型变量即可
结
且除法与其他不同,其他的函数内都是从0开始,这里是从后面开始,因为存入时,数据的高位在后面,除法要从高位开始
之后,是将所有的当前的数据加到 r 身上,然后push(r / b),且更新 r = r % b(更新余数)
最后要将其倒序,要将数据的高位放到容器末尾,这样方便去除前导0
main函数传参时:传入时,由于第三个参数是传出参数,所以直接传入一个int型变量即可
结
知识点1:他们都是根据具体情况,将当前的运算,全部存入 t 或者 r 中,然后拿着 t 或者 r 进行结果的压入,并更新 t 和 r,为下一次做准备
知识点2:加和乘法要额外注意,判断最后的 t ,如果循环结束,t还存在,那么要压入 1或者t
知识点3:减法和除法要额外注意,for循环之后,进行前导0的去除
知识点4:为了方便记忆以及前导0的去除,所以,我们统一在main函数,压入数据时,将数据的低位,先压入。也就是从string的末尾开始压入,表现为vector与string是反着的。
而输出时,由于我们统一将个位放在了C容器的栈底,所以,输出时,是从C容器的尾部开始输出
知识点五:在函数中,加减乘都是从个位开始计算,也就是for循环从0开始,而除是从高位开始计算,也就是从容器的末尾开始for循环,所以,在for循环结束后,要将其倒序,一方面是因为这样方便记忆,另一方面,这是去除前导0的前提要求
位运算(均是拷贝运算,不会影响原数据,这点要注意)
&、|、^
位运算特性+细节

首先,我们尝试不使用递归来解决这道题,他让我们判断是一个数是否为2的次幂。
尝试往位运算方面靠,位运算是通过二进制来解决问题的,而二进制就是2的次幂的表示,且,二进制从低位向高位,依次是2的012345…次方,所以,我们可以知道二进制表示为10000的数,(即第一位是1,后面全是0的数)是2的次幂数
所以,初步的认知已经建立了。之后寻找位运算的特性,如果一个数是1000的话,那么0111 + 1 就是 1000,而1000与0111做位与运算,可以得到0000,所以可以通过该性质找到10000特点的数
注意点1:小于等于0的数,可以直接排除
注意点2:进行位运算时,要在做完位运算之后,加一层括号,因为位运算的优先级低于==
知识补充
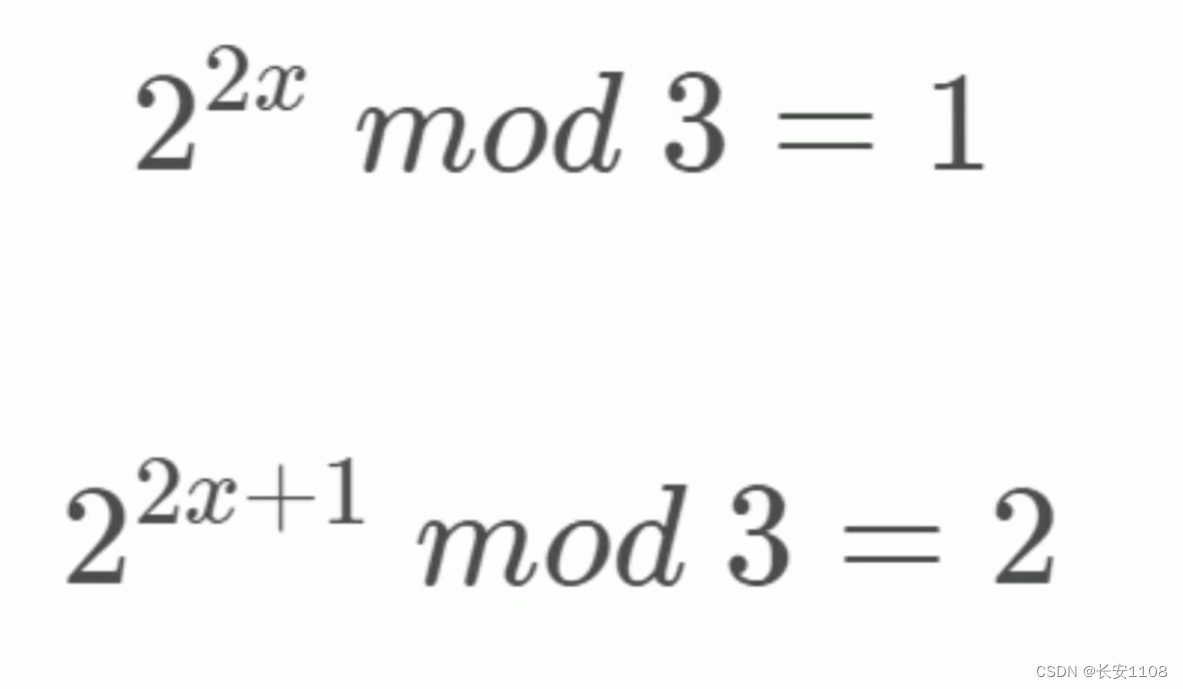
2的偶数次幂mod3等于1,例如4、16等,mod3 等于 1
而2的奇数次幂,就是2的偶数次幂再乘2,此时如8、32,mod3等于2
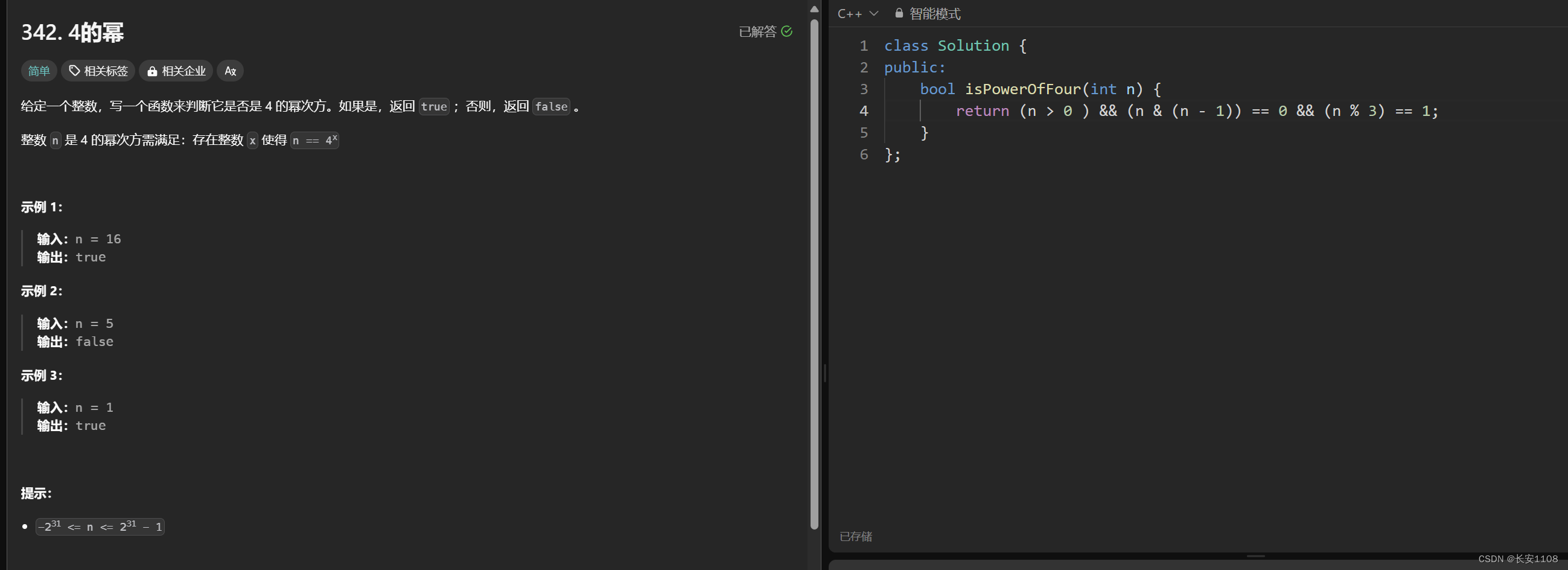
所以在求4的次幂时,因为2的偶次幂,一定是4的次幂,所以,我们在找到2的次幂数的基础上,再找到那些是2的偶次幂的数,那些数mod3==1
对于n-1的理解
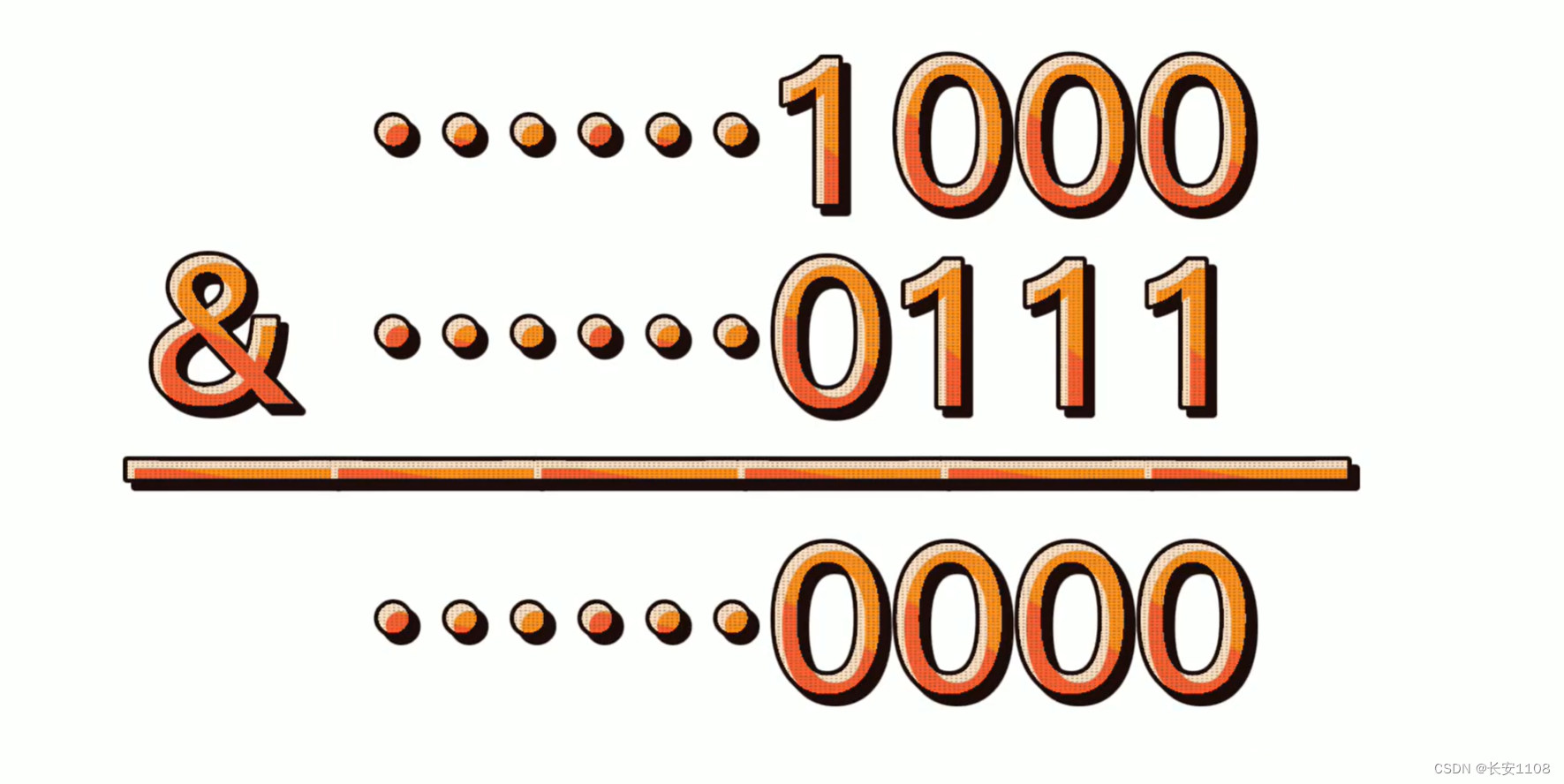
对于一个二进制 n = 10000010000101010,n - 1 = 10000010000101000,n - 1会将一个数的二进制表达最右边的1变为0,而其他不变,利用该特点可以得到1的个数
或者使用lowbit,见算法一栏“基础算法”(lowbit的时间复杂度更低)

异或来实现数字交换

首先,a = a ^ b,此后我们可以将一个a看成是变化之后的a,而如果a^b,则是原数据a、b
b = a ^ b,此时a是变化之后的a,将其拆开:a ^ b ^ b,此时a是变化之前的a,所以,就等于a ^ 0,最终等于原来的a
而到此时,a除了在第一行做出了改变,其他地方均无改变,所以,还是第一行的结论:可以将一个a看成是变化之后的a,而如果a^b,则是原数据a、b
所以,a = a ^ b,a是第一行代码执行后变化的a,b是原来的a,所以,将a拆开(得到原来的a 和 b)并且将b换成原来的a:a ^ b ^ a,再使用交换律,得到a ^ a ^ b,最后等于原来的b

找到只出现一次的数据,其余数据出现偶数次

首先定义res = 0;
之后将res与数组中的每个数进行异或运算
用到的知识点:
1、0^a = a
2、b^b = 0;
>> 、<<
二进制中相邻的位的特点


判断相邻位数是否交替为0、1
也就是相邻的位数上不能是相同的,即不能是00或者11,
而00对应于十进制是0,11对应于十进制是3
所以,如果 n&3 == 3,则表示当前n的右边两位是11
如果n&3 = = 0,则表示当前n的右边是00,(注意,此处还是&3,即00&11结果为00。逻辑上,他还有个等价式是00&00结果为11,也就是n&0 = = 3,但是如果&0的话,可能转为二进制就变成&一位0,而&3的话,铁定在二进制是&两位,所以,&0会导致某些数据点报错)
每次判断完之后,将n>>1右移一位,并覆盖到n,注意每次右移一位,如果右移两位,可能会出现0110,这样的数据,会出错
注意点1:&运算一次进行多位二进制判断时,尽量避免&0,尽可能找其等效式
注意点2:从此处我们也可以看出,我们之前的x&1,就是利用&的原始定义来求的,最终求出x二进制的个位,因为1表示成二进制就是…00001
找出某个排列的所有子集

我们以一个存有三个数的数组为例,那么nums.size()就等于3,而他的子集可能会是没有元素,或者一个元素,或者两个,或者三个,如果我们挨个遍历的话,时间复杂度肯定会剧增,所以,我们利用二进制,即利用位运算

我们可以将某个数在or不在,表示为二进制上的1or0,现在我们已经有了不同的子集与二进制的对应,那么如何进行遍历呢,我们可以让
i 从 0 遍历到 小于(1 << size()),因为1左移size位,就变成了1000,他正好就是四位的第一个数,所以小于他的,就是所有0位1位2位3位的二进制,也就是下图所示情况。这样,每个 i 的二进制,都标识了一种数组子集的情况


有了这些 i 的循环,我们如何判断当前是哪个二进制位上为1呢,我们可以在每个i循环步内,定义一个 j 循环,j 从 0 到小于size,
他实际上数组下标,判断 i & (1 << j)是否为1,而(1 << j)的循环是 001、010、100,如果结果不为0,那么就是为1,即当前循环步的 i的二进制标识,与当前 j 二进制中为1的那一位,都是1,即表明,i 中对应 j 为1 的位置是1,则nums[ size - j - 1 ]就是当前子集的元素之一
但是注意,他的顺序不是“先是单个元素,然后两个,三个”,他会先输出两个单元素,再输出一个双元素,再输出一个单元素,…无规则的,因为3对应二进制11,肯定会得到两个数
如果想要从左边开始判断,适当修改 i 和 j 的循环方向
栈
题

结
知识点1:tt初始化为0,那么栈顶元素就是从1开始,所以栈不为空的话,就是tt>0,而下标0的位置没有被使用
当然我们也可以使得tt初始化为-1,那么栈顶元素就是从0开始,tt>=0时,不空
知识点2:栈可以解决那些,需要一边进行输入一边进行匹配的问题
知识点3:注意特判,要保证 i > 0时,再进行check。所以说,有时候并不一定要设计出多优雅全能的代码,哪里有问题就解决哪里就好了
单链表
题

结
知识点1:主要就是将一些插入手法(头插、随机插),删除,初始化等等操作熟悉起来
知识点2:要注意初始化,如果一道题中,已知了链表的全貌,那么在一开始就可以把链表构造出来,head表示头指针,是头结点的下标。然后最后一个结点的ne数组值是-1
知识点3:如果后续还要有新的节点加入进来,那么初始化时,head就可以初始化为-1。后续有节点插入后,就会自然形成尾节点的ne数组值是-1
知识点4:注意遍历方式
知识点5:ne等这些与其他节点有联系的操作,都是通过下标联系,即地址,只有少数情况会用到e数值
注意点1:本题是在原本的链表内操作,在把x插到头结点的同时,还会把x从原来的地方删除,所以,每次操作涉及插入和删除两个动作
双链表
题

结
知识点1:因为链表的优越性,也就是其在物理位置上的顺序无所大谓,他的顺序是由指针域决定的,所以,我们会将e数组的0号位置设置为头结点,1号位置是尾节点,但是这两个点在e数组上并没有值,他们仅仅代表头指针和尾指针所指的位置,且对于双链表,我们设置了l【】和r【】数组,所以,初始化时,r[0] = 1, l[1] = 0,表示头指针位置指向尾指针位置,尾指针位置指向头指针位置
知识点2:

在k的右边插入:顺序是:
先新建一个结点,之后设置新节点的r 和 l (因为这个比较好设置)
其次,就是选择更新旧结点的r 和 l 了,但是如何选呢,有个好的记忆方法是,因为让我们在k的右边插入,所以,r[k] 是我们拿到右边旧结点的关键信息,他会贯穿整个过程,所以,他应该最后一个被更新,所以,在k的右边插入,就最后更新r[k]
知识点3:对于双向链表,插入是需要注意顺序的,但是删除不需要注意顺序
知识点4:对于双链表的遍历,从 i = r[0]开始,当 i != 1时,i = r[ i ]
注意循环条件不要写成r[ i ] != 1,这样的话,最后一个元素将不会输出
知识点5:至于要不要构建循环双链表,则视题目情况而定(构建方式,加一个l[0] = 1, r[1] = 0,其他操作不变)
队列
二级目录
二级目录
哈希表
题
结
可能是用于,处理一些集合,该集合的特点是,数据少,但是数据有很大的也有很小的,将其哈希到一个比较紧凑的区域,节省空间和效率
思考:有没有可能可以使用set or multiset代替?
字符串哈希
题

结
他主要是将前 i 个字符组成的子串哈希成一个ULL值,再根据【l, r】的哈希值是h[r] - h[l - 1]*p[r-(l - 1)]这个公式,从而可以迅速的求出任意一段子串
知识点1:该计算公式用于字符串从1位置开始存储,所以,我们在写程序时,要写从1开始输入字符串,但是如果题目要求从0开始输入,且题目据此规则进行查询,那么无需改动其他的,只需要在读入l1,r1,l2,r2后,传入get函数l1 + 1,r1 + 1,l2 + 1,r2 + 1,即可
知识点2:要注意大写P=131,小写p是数组,表示p的某次方
知识点3:预处理:初始化在全局位置,所以p[]和h[]都是0,在预处理之前,我们要修改p[0] = 1,不然所有的p都是0,h不用修改,预处理时,处理 i 从1到N(或者题目若给出了字符串长度n,则是到等于n,如果拿不准,直接N也可以),注意p和h的预处理都建立在i - 1之上,别写错了
知识点4:h数组和p数组都是ULL,对于无符号整形的变量,如果超出了其表示范围,那么会对其进行自动取模,所以,这里存入ULL类型,是为了自动取模2的64次方(该自动取模只会使用与无符号整型,且如果遇到负数 则还会将其先加上模数变为整数 再取模)
