滑动窗口求最大和最小
滑动窗口
要区分最小和最大滑窗,内层while循环的条件和更新结果的地方
核心:
关键的区别在于,最大滑窗是在迭代右移右边界的过程中更新结果,而最小滑窗是在迭代右移左边界的过程中更新结果。
最小滑窗
给定数组 nums,定义滑窗的左右边界 i, j,求满足某个条件的滑窗的最小长度。
while j < len(nums)://这个while也可用fori代替判断[i, j]是否满足条件while 满足条件:不断更新结果(注意在while内更新!)i += 1 (最大程度的压缩i,使得滑窗尽可能的小)j += 1
L209长度最小的子数组
-
题目:给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例:
输入:s = 7, nums = [2,3,1,2,4,3] 输出:2 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
提示:
- 1 <= target <= 10^9
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 10^5
-
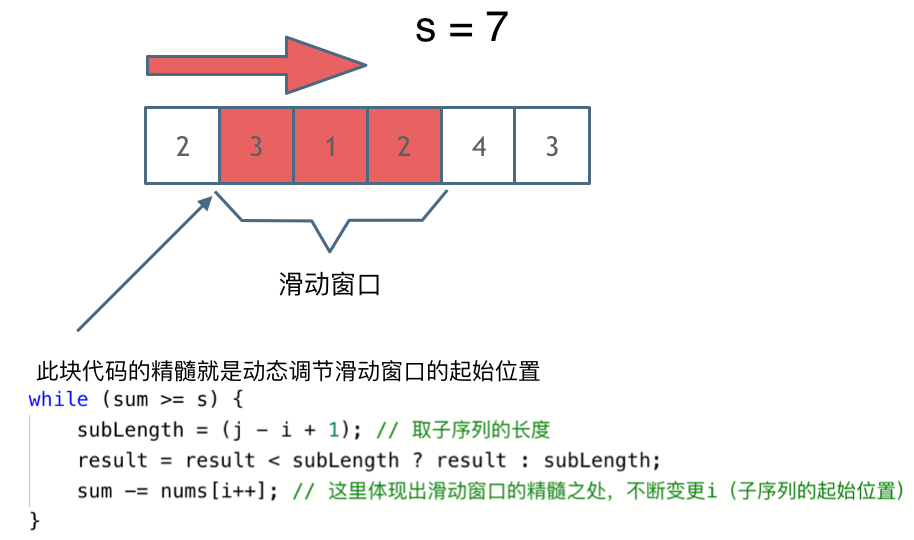
-
class Solution {// 滑动窗口public int minSubArrayLen(int s, int[] nums) {int left = 0;int sum = 0;int result = Integer.MAX_VALUE;for (int right = 0; right < nums.length; right++) {sum += nums[right];//这里要求的是最小子数组,所以这里的while是满足条件的//然后在while里面最大程度的压缩i(也就是左边界)while (sum >= s) {result = Math.min(result, right - left + 1);sum -= nums[left++];}}return result == Integer.MAX_VALUE ? 0 : result;} }
最大滑窗
给定数组 nums,定义滑窗的左右边界 i, j,求满足某个条件的滑窗的最大长度。
while j < len(nums):判断[i, j]是否满足条件while 不满足条件:i += 1 (最保守的压缩i,一旦满足条件了就退出压缩i的过程,使得滑窗尽可能的大)不断更新结果(注意在while外更新!)j += 1
L904水果成蓝
-
你正在探访一家农场,农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示,其中 fruits[i] 是第 i 棵树上的水果 种类 。
你想要尽可能多地收集水果。然而,农场的主人设定了一些严格的规矩,你必须按照要求采摘水果:
你只有 两个 篮子,并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
你可以选择任意一棵树开始采摘,你必须从 每棵 树(包括开始采摘的树)上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次,你将会向右移动到下一棵树,并继续采摘。
一旦你走到某棵树前,但水果不符合篮子的水果类型,那么就必须停止采摘。
给你一个整数数组 fruits ,返回你可以收集的水果的 最大 数目。 -
白话题目:求只包含两种元素的最长连续子序列
-
class Solution {public int totalFruit(int[] fruits) {int n = fruits.length;Map<Integer, Integer> cnt = new HashMap<Integer, Integer>();int left = 0, ans = 0;for (int right = 0; right < n; ++right) {cnt.put(fruits[right], cnt.getOrDefault(fruits[right], 0) + 1);//注意这里的while是不满足条件的//并且这里统计的ans是在while外面进行更新的!!!!!//这个与上面的最小子数组有着本质区别while (cnt.size() > 2) {cnt.put(fruits[left], cnt.get(fruits[left]) - 1);if (cnt.get(fruits[left]) == 0) {cnt.remove(fruits[left]);}++left;}ans = Math.max(ans, right - left + 1);}return ans;} }
总结:
-
第一题让求大于某个数的最小子数组长度
-
while里面最大限度的压缩,只要满足就压缩
-
while的条件是大于某个数(即满足题意),并且while每循环一次就更新一下result的长度
-
while (sum >= s) {result = Math.min(result, right - left + 1);sum -= nums[left++];}
-
-
第二题让求最多包含两类(<=2)的最长子序列长度
-
while里面最小程度的压缩
-
while里的条件是大于2(即与题意相反),并且是while结束后进行更新长度ans
-
while (cnt.size() > 2) {cnt.put(fruits[left], cnt.get(fruits[left]) - 1);if (cnt.get(fruits[left]) == 0) {cnt.remove(fruits[left]);}++left;}ans = Math.max(ans, right - left + 1);
-
