剑指 Offer 62. 圆圈中最后剩下的数字
摘要
剑指 Offer 62. 圆圈中最后剩下的数字
一、约瑟夫环解析
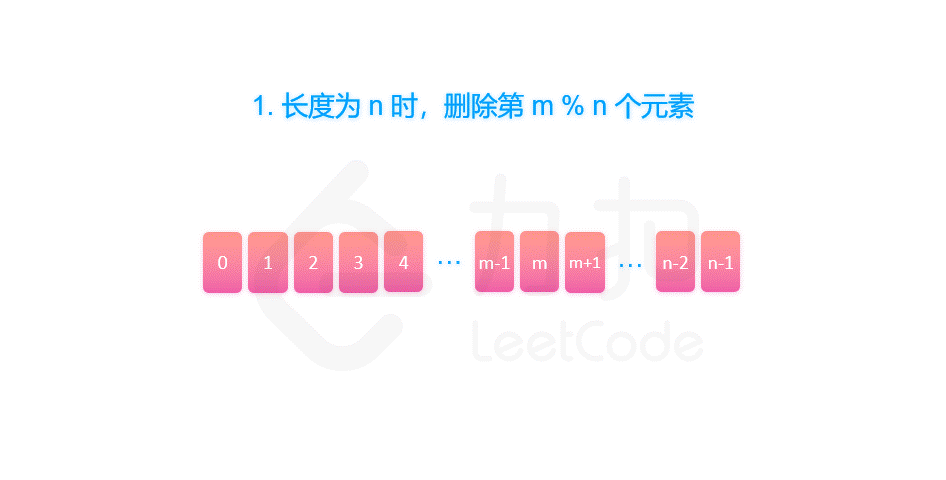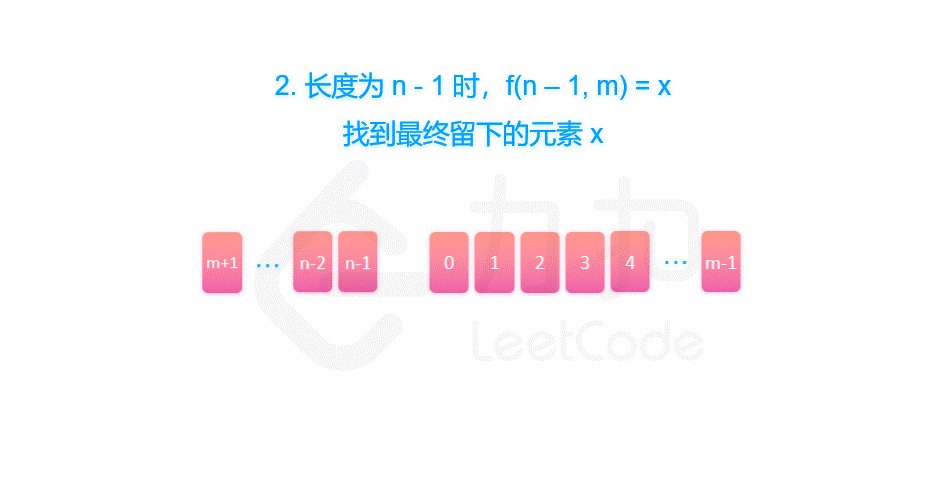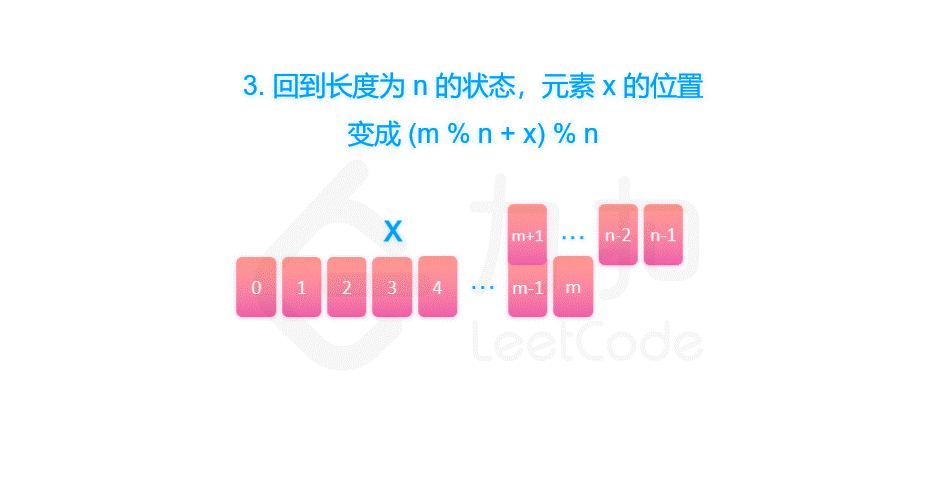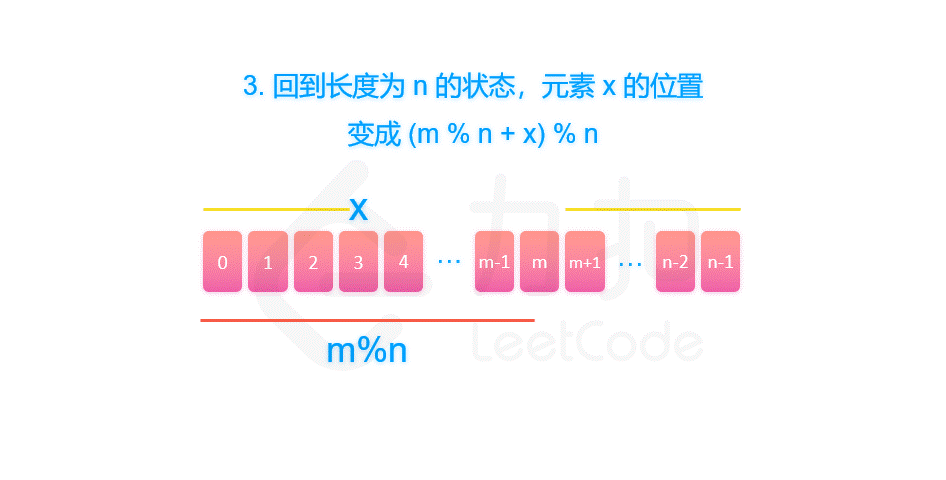
题目中的要求可以表述为:给定一个长度为 n 的序列,每次向后数 m 个元素并删除,那么最终留下的是第几个元素?这个问题很难快速给出答案。但是同时也要看到,这个问题似乎有拆分为较小子问题的潜质:如果我们知道对于一个长度n - 1 的序列,留下的是第几个元素,那么我们就可以由此计算出长度为 n 的序列的答案。
我们将上述问题建模为函数 f(n, m),该函数的返回值为最终留下的元素的序号。
首先,长度为n的序列会先删除第m% n 个元素,然后剩下一个长度为n - 1的序列。那么,我们可以递归地求解 f(n - 1, m),就可以知道对于剩下的 n - 1 个元素,最终会留下第几个元素,我们设答案为 x = f(n - 1, m)。
由于我们删除了第 m % n 个元素,将序列的长度变为 n - 1。当我们知道了 f(n - 1, m) 对应的答案 x 之后,我们也就可以知道,长度为 n 的序列最后一个删除的元素,应当是从 m % n 开始数的第 x 个元素。因此有 f(n, m) = (m % n + x) % n = (m + x) % n。
我们递归计算 f(n, m), f(n - 1, m), f(n - 2, m), ... 直到递归的终点 f(1, m)。当序列长度为 1 时,一定会留下唯一的那个元素,它的编号为 0。
class Solution {public int lastRemaining(int n, int m) {return f(n, m);}public int f(int n, int m) {if (n == 1) {return 0;}int x = f(n - 1, m);return (m + x) % n;}
}复杂度分析
- 时间复杂度:O(n),需要求解的函数值有n个。
- 空间复杂度:O(n),函数的递归深度为n,需要使用 O(n)的栈空间。
二、数学 + 迭代
class Solution {public int lastRemaining(int n, int m) {int f = 0;for (int i = 2; i != n + 1; ++i) {f = (m + f) % i;}return f;}
}复杂度分析
-
时间复杂度:O(n),需要求解的函数值有n个。
-
空间复杂度:O(1),只使用常数个变量。
博文参考
《leetcode》
