图像处理_积分图
目录
1. 积分图算法介绍
2. 基本原理
2.1 构建积分图
2.2 使用积分图
3. 举个例子
1. 积分图算法介绍
积分图算法是图像处理中的经典算法之一,由Crow在1984年首次提出,它是为了在多尺度透视投影中提高渲染速度。
积分图算法是一种快速计算图像区域和以及图像区域平方和的算法。直白的说,就是很快计算一幅图像任意区域,也就是卷积区域下的像素值的和跟平方和。它的核心思想就是对每一个图像建立起自己的积分图查找表,在图像处理的阶段就可以根据预先建立积分图查找表直接查找,从而实现对均值卷积的线性时间计算。做到了卷积执行的时间与半径窗口大小的无关联。
利用积分图可以极大地加快计算原始图像中任一矩形区域的像素和,因为只需经过一次计算。这种算法被应用到基于NCC的快速匹配、对象检测和SURF变换中、基于统计学的快速滤波器等方面。第一个应用积分图像技术的应用是在Viola-Jones的对象检测框架中出现。
2. 基本原理
在积分图中,我们需要做两个操作:
1)构建积分图
2)使用积分图
2.1 构建积分图
如上图所示,S(x,y)对应于(x,y)跟左上角原点(0,0)所包围的区域的图像灰度总和。从左上角开始,我们可以根据如下公式推算整个图像的积分图。原始图像(x,y)位置对应的积分值为:
![]()
积分图是由 “每个像素位置(x,y)对应的与原点(0,0)组成的矩形区域内的图像灰度和(称为积分值)” , 组成一个一个新的"图像"。
2.2 使用积分图
如上图所示,为了求该矩形区域的灰度之和。我们可以用以下公式表示:
![]()
这里的总和并不包含点A,B,C的像素值。如上图所示的小像素点,A,B,C所在的像素点不在矩形区域以内。
3. 举个例子
原始(灰度)图像 与 积分图像
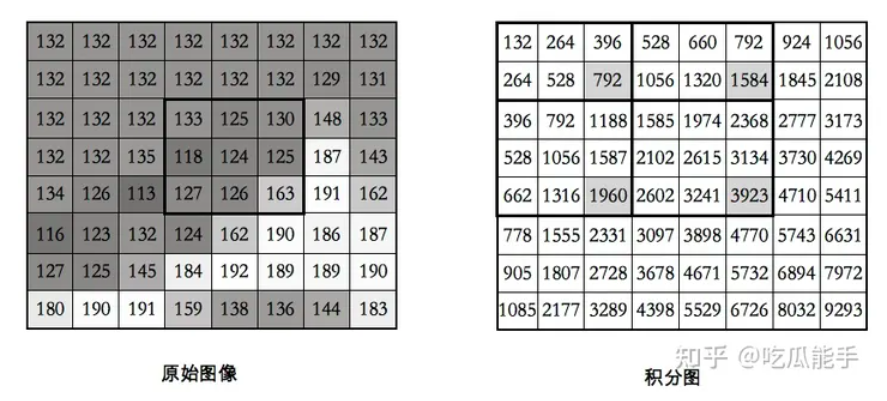
其中:图像位置(1,1)对应的积分值 I(1,1) = 528 的计算方法为:
S(1,1) = I(1,1) + S(0,1) + S(1,0) - S(0,0) = 132(原图中(1,1)位置灰度值) + 264(积分图中(0,1)位置积分值) + 264(积分图中(1,0)位置积分值) - 132(积分图中(0,0)位置积分值) = 528
则求下面区域的图像像素灰度值Sum(A) = 等于多少?如何求?
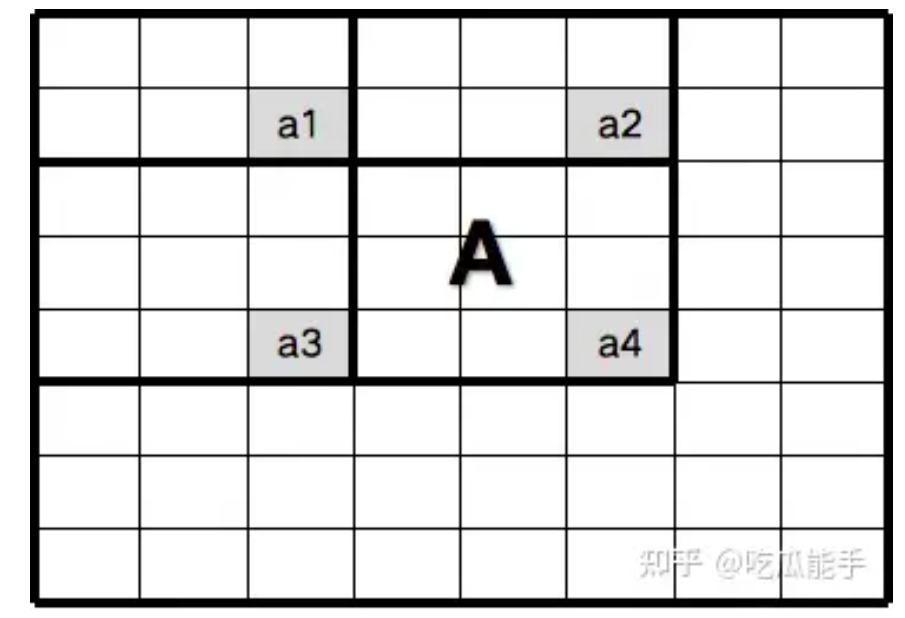
则 Sum(A) = S(6,5) +S(3,2) -S(3,5) - S(6,2) = 3923 + 792 – 1584 – 1960 = 1171,
可以在原始图像验算下: 133 + 125 + 130 + 118 + 124 + 125 + 127 + 126 + 163 = 1171, 正确
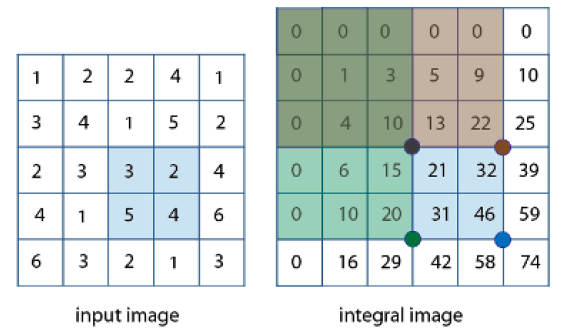
注意:计算积分图第一行,第一列时,对于上方和右方越界的像素点,灰度设为0 ,图示如下:
对应python函数:
python中对应的函数为cv2.integral(返回sum)。根据输出需要,还有两个可选函数cv2.integral2(返回sum与平方和)和cv2.integral3(返回sum、平方和以及旋转45度)。
参考:
【OpenCV】28 图像积分图算法_opencv 图像平方和-CSDN博客
【图像处理】积分图像及其应用_对图像矩阵做积分图怎么做,给出例子-CSDN博客
图像检测入门(五)积分图 - 知乎


