当前位置：首页 > news >正文

蓝桥杯练习07小兔子爬楼梯

news 2025/7/22 17:29:05

小兔子爬楼梯

介绍

小兔子想去月球上旅行，假设小兔子拥有一个阶梯子，当你爬完层就可以到达月球，小兔子每次可以跳1或者2个台阶，小兔子有多少种跳法可以到达月球呢？
给定n是一个正整数，代表梯子的阶数，当n=2时，小兔子有2种跳法到达月球；当=3时，小兔子有3种跳法跳到月球，以此类推，解释如下图所示：

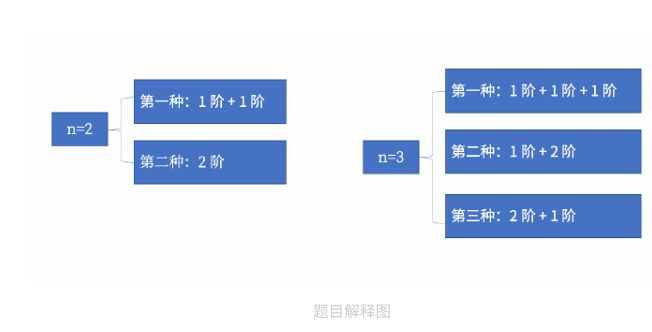
提示

这里为同学提供一种解题思路。

递归
可以使用递归来实现，具体思路如下：
. 当阶梯数为0时，只有0种方法；当阶梯数为1时，只有1种方法；当阶梯数为2时，只有2种方法，所以当阶梯数小于等于2时，可以直接返回值。
·如果阶梯数大于2，就递归。
解题思路不只这一种，同学们可以自由发挥。

准备

开始答题前，需要先打开本题的项目代码文件夹，目录结构如下：

其中：
·js/index.js是实现函数的is代码文件。
·index.html是显示结果的页面。
在浏览器中预览index.html页面效果如下：

目标

请完善js/index.js文件中的代码，让页面呈现如下所示的效果：

代码

html

<!DOCTYPE html>
<html lang="en"><head><meta charset="UTF-8" /><meta name="viewport" content="width=device-width, initial-scale=1.0" /><title>Document</title></head><body><div><p id="result1"></p><p id="result2"></p><p id="result3"></p></div><script src="./js/index.js"></script><script>let r1 = document.getElementById("result1");let r2 = document.getElementById("result2");let r3 = document.getElementById("result3");r1.innerHTML = `2 阶梯子，兔子有 ${climbStairs(2)} 种跳法到达月球。`;r2.innerHTML = `3 阶梯子，兔子有 ${climbStairs(3)} 种跳法到达月球。`;r3.innerHTML = `4 阶梯子，兔子有 ${climbStairs(4)} 种跳法到达月球。`;</script></body>
</html>

js

const climbStairs = (n) => {// TODO：请补充代码/*** 思路：分析可得第n阶梯子的跳法等于第n-1和第n-2阶梯子的跳法之和*/
};
module.exports = climbStairs;

答案

const climbStairs = (n) => {// TODO：请补充代码/*** 思路：分析可得第n阶梯子的跳法等于第n-1和第n-2阶梯子的跳法之和*///法一：递归思想if (n <= 2) {return n} else {return climbStairs(n - 1) + climbStairs(n - 2)}//法二：第1阶梯子有一种跳法 第2阶梯子有2种跳法，用a，b往后移代表第n-1和第n-2阶梯子的跳法// if (n <= 2) {//     return n// }// let a = 1// let b = 2// let c// while (n > 2) {//     c = a + b//后移a，b//     a = b//     b = c//     n--// }// return c//法三：利用解构赋值，整体思想与法二一样// if (n <= 2) {//     return n// }// let a = 1// let b = 2// while (n > 2) {//     // 解构赋值//     [b, a] = [a + b, b]//     n--// }// return b};
module.exports = climbStairs;