常见数据结构
一. 数据结构概述、栈、队列
1. 数据结构概述


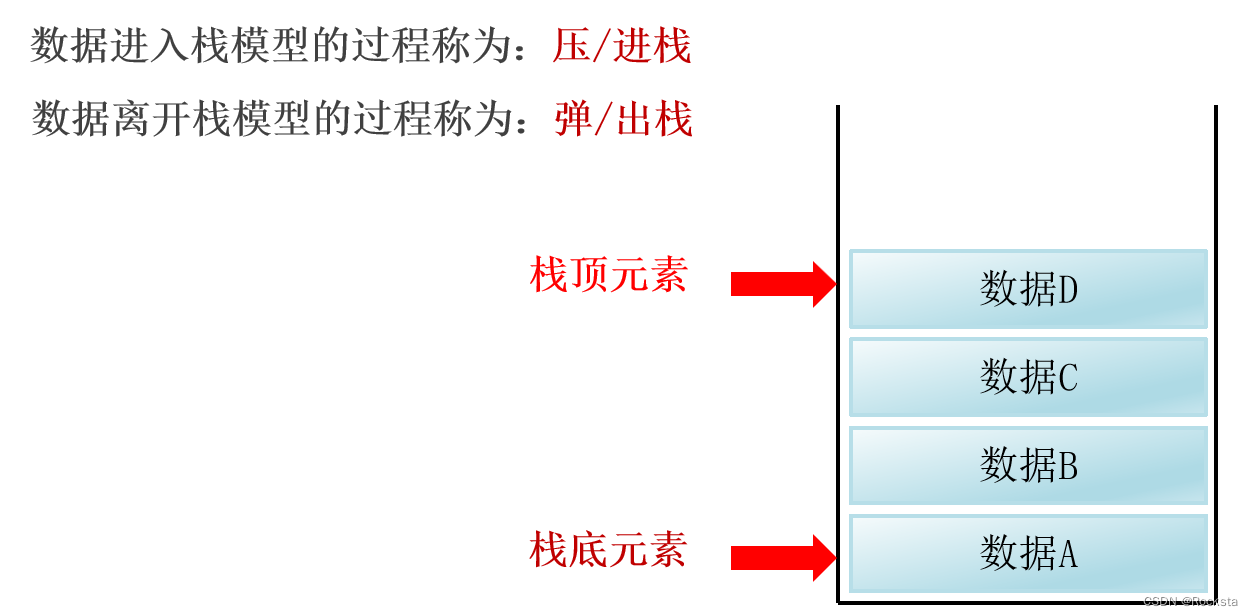
2. 栈数据结构的执行特点


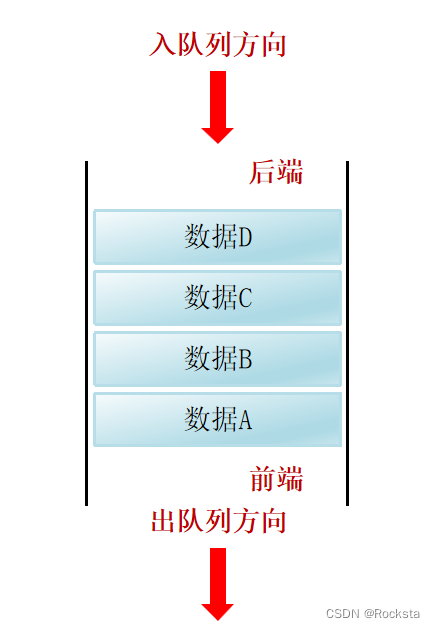
3. 常见数据结构之队列


二. 常见数据结构之数组
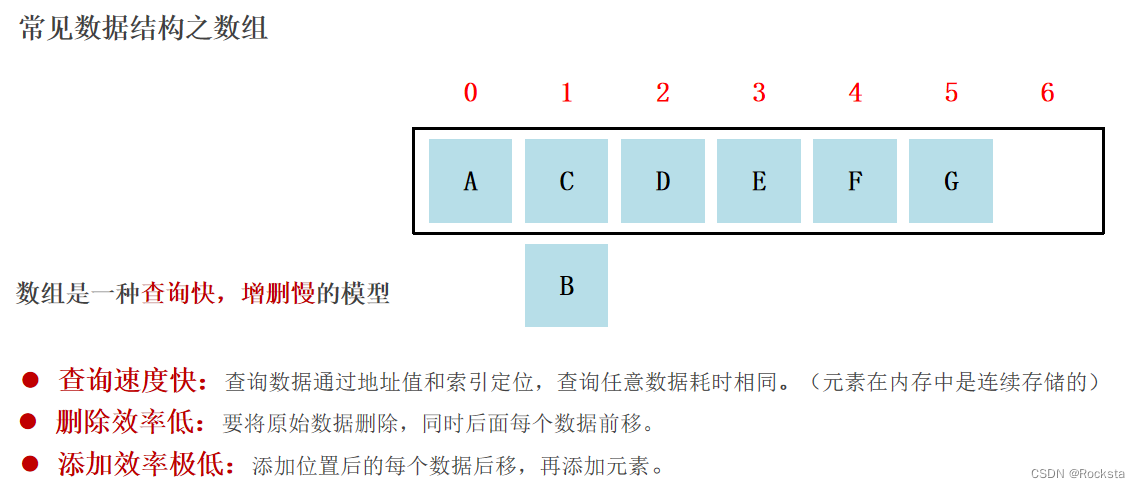
- 数组它就是内存中的一块儿连续区域。
- 数组变量存的是数组在堆内存当中的起始地址。
- 数组查询任意索引位置的值耗时相同,数组根据索引查询速度快。
- 数组是一种根据索引查询快,增删慢的模型。
- 数组增删元素要对元素进行移位,甚至可能要创建新数组。
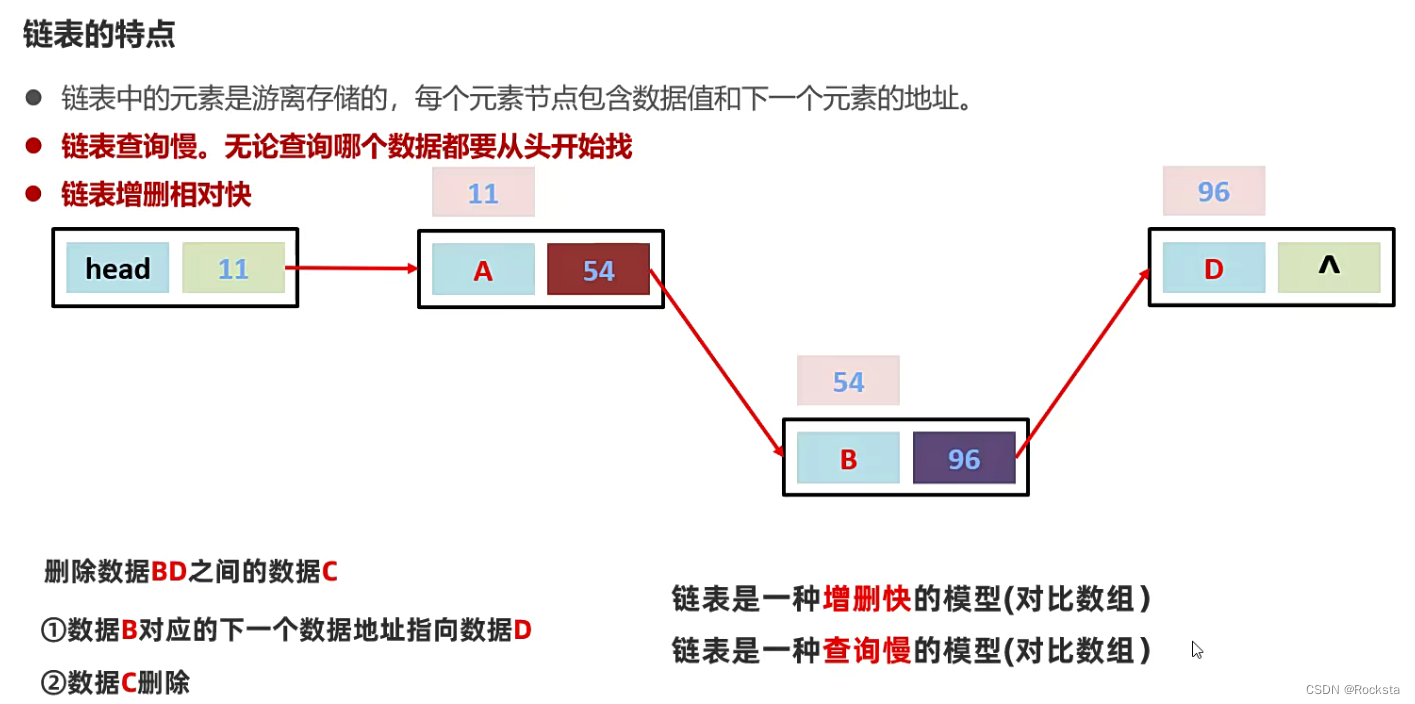
三. 链表
- 链表中的每个元素节点首先是包含了自己的节点的地址,每个元素节点的内部包含了自己的数据值和下一个元素的地址。

- 头地址指向链表中的第一个元素。

- 链表只是增删那一刻相对来说比较快,增删数据要找到这个数据才能删,找的过程也就是查询的过程还是比较慢的。

链表的分类:
- 单向链表:只能从前往后找。
- 双向链表:从前可以往后找,从后也可以往前找。有个头地址,有个尾地址,头可以往后找,尾可以往前找。Java中双链表用的比较多。增删首尾元素的速度特别快。因为双链表可以直接定位首尾元素。
- 结论:数组根据索引查元素是最快的,而双链表增删首尾元素的速度是最快的。

四. 二叉树和二叉查找树
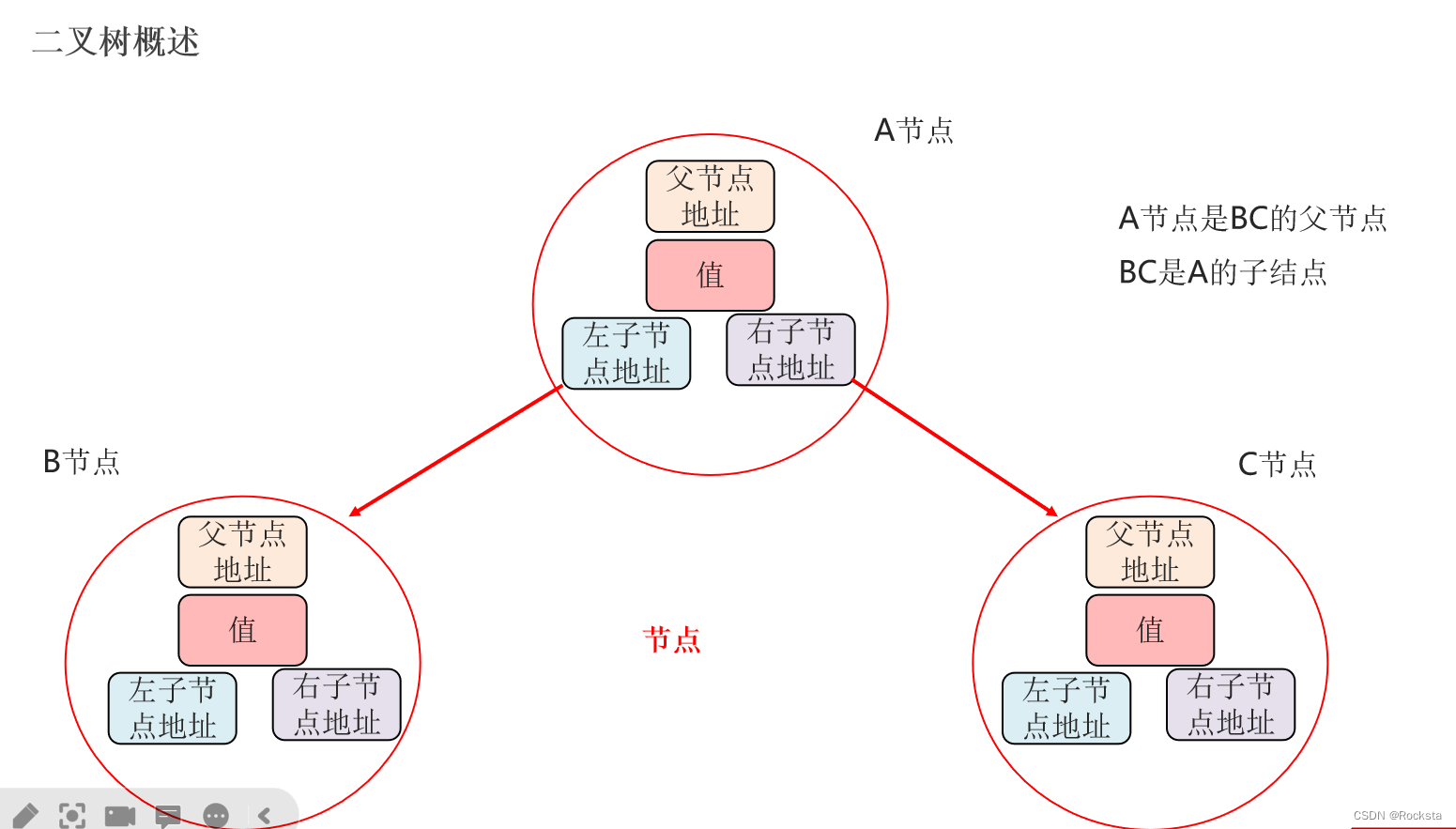
- 二叉树和二叉查找树是我们后面一些特殊集合的底层数据结构。
- 二叉树是包含一个父节点,父节点产生一个左节点,还有一个右节点。每个节点最多只能有两个子节点,分别是左子节点和右子节点。
- 如果是根节点,它的父节点地址值就为null。
放了数据的二叉树:

二叉查找树:
- 二叉查找树它小的会往左边走,大的会往右边走。
- 二叉查找树它是一种二分查找的算法,目的:为了提高检索数据的性能。
- 二叉查找树又称二叉排序树或者二叉搜索树。
- 因为二叉查找树它小的会往左边走,大的会往右边走,因此左子树上所有节点的值都小于根节点的值,右子树上所有节点的值都大于根节点的值。
- 普通二叉树不怎么用,开发中用的最多的还是二叉查找树。

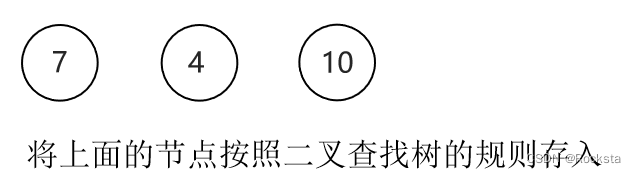
二叉查找树节点添加的一个机制:
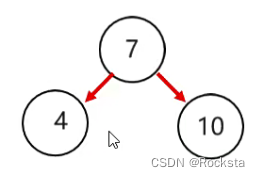
- 规则:小的存左边,大的存右边,一样的不存。
- 将7作为根节点,4比7小往左边走,10比7大往右边走。
- 二叉查找树是一个增删改查都挺快的一个数据结构,相对来说比较完美,包括后续数据库检索数据也会用到这种数据结构。
五. 平衡二叉树(比较完美的一种二叉树结构)
二叉查找树存在的问题:

-
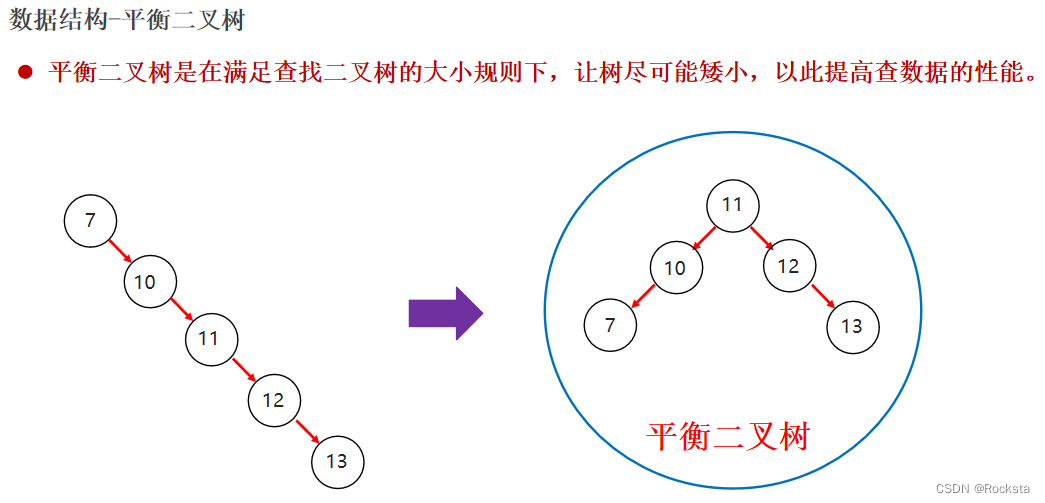
我们发现排好之后这个二叉查找树相当于是一个链表,而链表的话查询速度就慢了。
- 问题:出现瘸子现象,导致它的查询性能与单链表一样,查询速度变慢!

- 我们希望这个树它能在满足二叉树的规则之上,能够尽量的矮小,因为树越矮,去搜索的深度就会越短,可以提高检索的性能。
- 而平衡二叉树的目的就是为了把这个数做的尽量矮小,数据的分布尽量的均匀。
如何去满足成为一颗平衡二叉树:
- 平衡二叉树要求任意节点的左右两个字数的高度差不超过1,这样可以使元素分布的尽量均匀,把树做的尽量矮小。

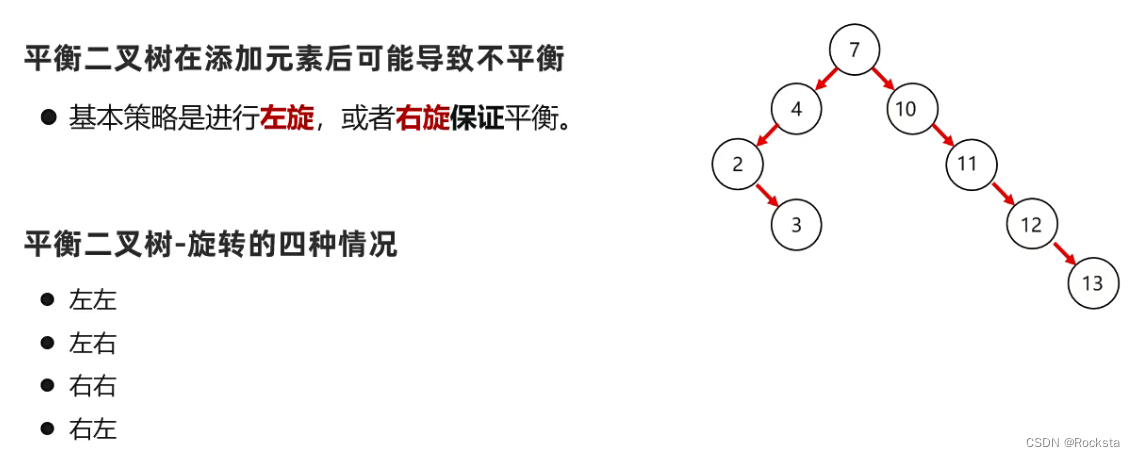
- 思路:左边高,右拉。右边高,左拉。
- 左边高,右拉,右拉不行,就放弃右拉,先以不平衡的那个点左拉再整体右拉,反之亦然。
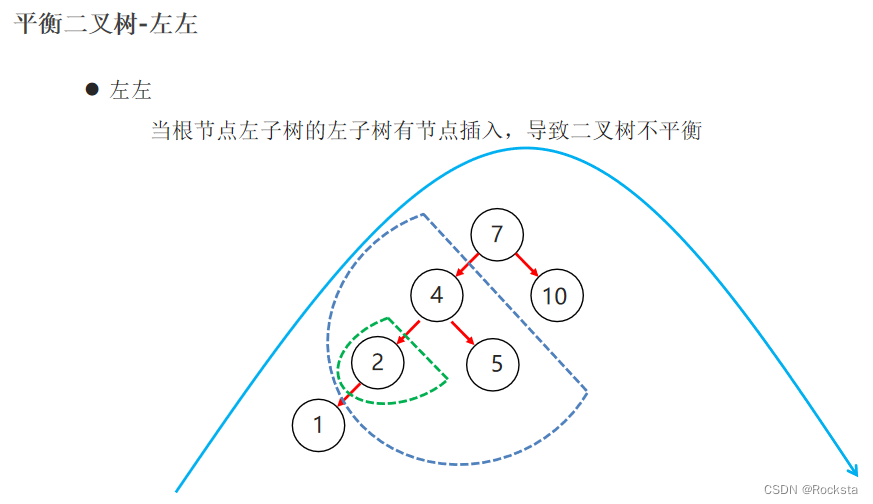
案例:使1234567成为一颗平衡二叉树: 4 2,6 1,3,5,7

六. 红黑树
- 红黑树与平衡二叉树的目的一样,都是为了提高数据的增删改查的性能。
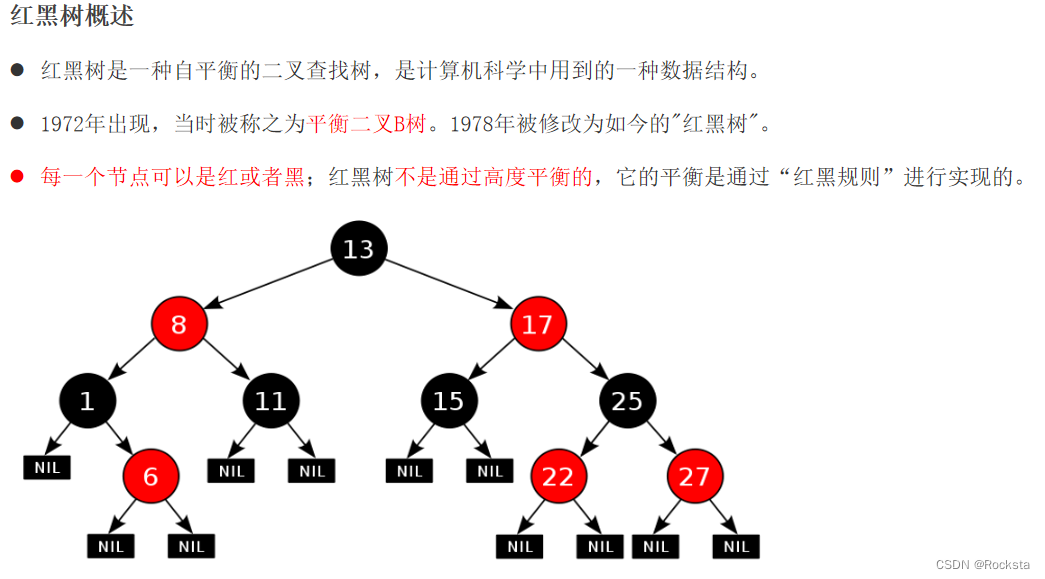
- 红黑规则:黑红黑红交替的。
- 红黑树的每一个节点要多一个字段值来标记它是什么颜色。后面去看Java底层代码也能看到,有些是基于红黑树的,它的节点里面是有这种red,black这样的属性的。
- 路径算法:每条路径均包含相同数目的黑色节点。
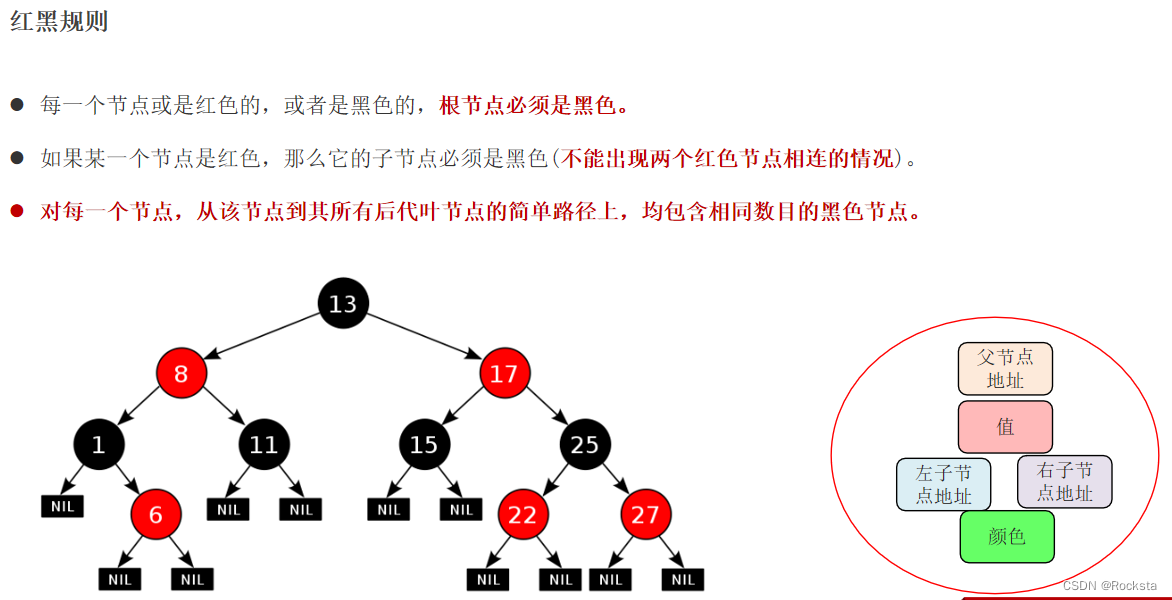
怎样去通过红黑规则来保持平衡?



