理解树的结构-算法通关村
理解树的结构-算法通关村
1.树的结构
- 树是一个有n个有限节点组成一个具有层次关系的集合,每个节点有0个或者多个子节点,没有父节点的节点称为根节点,也就是说除了根节点以外每个节点都有父节点,并且有且只有一个。树的种类比较多,最常见的是二又树,基本结构如下:
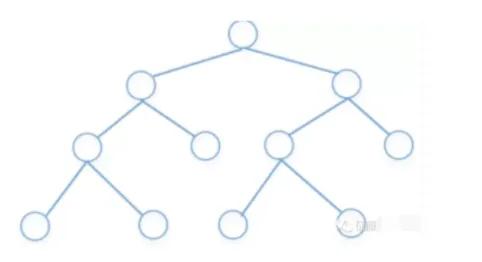
- 参考上面的结构,可以很方便的理解树的如下概念:
- 节点的度:一个节点含有的子节点的个数称为该节点的度;
- 树的度:一棵树中,最大的节点的度称为树的度,注意与节点度的区别;
- 叶节点或终端节点:度为0的节点称为叶节点;
- 非终端节点或分支节点:度不为0的节点;
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
- 节点的祖先:从根到该节点所经分支上的所有节点;
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林:由m(m>=0)棵互不相交的树的集合称为森林;
- 无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树;
- 有序树:树中任意节点的子节点之间有顺序关系,这种树称为有序树;
- 二叉树:每个节点最多含有两个子树的树称为二叉树;
2 树的性质
- 性质1:在二叉树的第i层上至多有2^(i-1)个结点(i>0)
性质2:深度为k的二叉树至多有2^k -1个结点(k>0)
性质3:对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则N0=N2+1;
性质4:具有n个结点的完全二叉树的深度必为 log2(n+1)
性质5:对完全二叉树,若从上至下、从左至右编号,则编号为i的结点,其左孩子编号必为2i,其右孩子编号必为2i+1;其双亲的编号必为i/2(i=1 时为根,除外) - 满二叉树就是如果一棵二叉树只有度为0的节点和度为2的节点,并且度为0的节点在同一层上,则这棵二叉树为满二叉树。

- 这棵二又树为满二叉树,也可以说深度为k=4,有2^k-1=15个节点的二又树。完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大 值,并且最下面一层的节点都集中在该层最左边的若干位置。
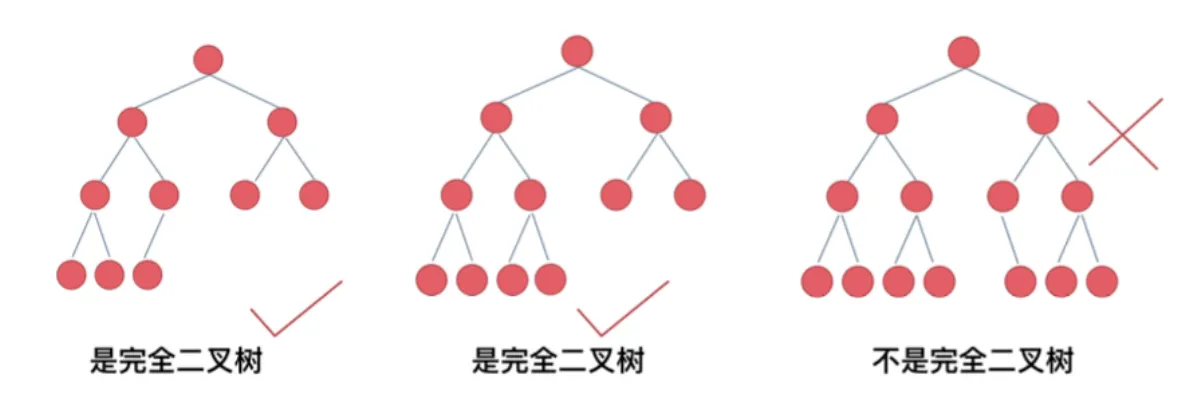
3 树的定义
-
定义二叉树
-
public class TreeNode {int val;TreeNode left;TreeNode right;} -
定义N叉树
-
public class Node {public int val;public List<Node> children;}
4树的遍历方式
- 二叉树的遍历方式有层次遍历和深度优先遍历两种:
• 深度优先遍历:先往深走,遇到叶子节点再往回走。
•广度优先遍历:一层一层的去遍历,一层访问完再访问下一层。
这两种遍历方式不仅仅是二叉树,N树叉也有这两种方式的,图结构也有,只不过我们更习惯叫广度优先和深度优先,本质是一回事。
深度优先又有前中后序三种,记住一点:前指的是中间的父节点在遍历中的顺序,只要大家记住前中后序指的就是父节点在访问中的顺序就可以了。
前序遍历:中左右 中序遍历:左中右 后序遍历:左右中 
5 通过序列构造二叉树
- 前面我们已经介绍了前中后序遍历的基本过程,现在我们看一下如何通过给出的序列来恢复原始二叉树,看三个序列:
(1)前序:1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2)中序:3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
(3) 后序:8 7 6 5 4 3 2 10 15 14 13 12 11 9 1
5.1前中序列复原二叉树
-
先看如何通过前中序列复原二叉树:
-
(1)前序:1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2)中序:3 4 8 6 7 5 2 1 10 9 11 15 13 14 12 -
第一轮 -
我们知道前序第一个访问的就是根节点,所以根节点就是1。
中序遍历的特点是根节点的左子树的元素都在根节点的左侧,右子树的元素都在根节点的右侧,从中序遍历序列我们可以划分成如下结构: -
前序中序划分: 中序序列划分:[3 4 8 6 7 5 2 ] 1 [10 9 11 15 13 14 12] 前序序列划分:1 [2 3 4 5 6 8 7] [9 10 11 12 13 15 14] -
上面前序序列第一个括号里的都是左子树的元素,第二个括号一定都是右子树的元素。参照中序的两个数组划分的。我们看到前序中7之前的元素都在中序第一个数组中,9之后的所有元素就在第二个数组种,所以我们从7和9之间划分。
由此,画图表示一下此时知道的树的结构为: -
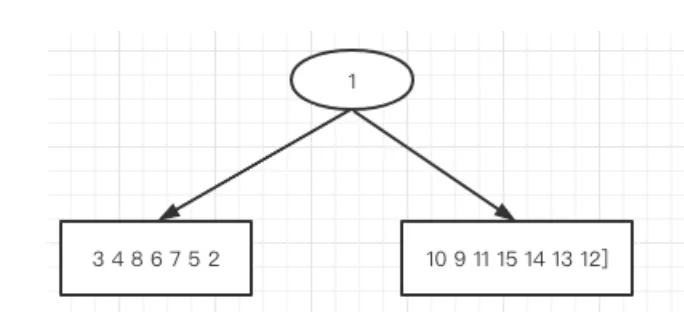
-
第二轮 -
我们先看两个序列的第一个数组:
前序:2 3 4 5 6 8 7 中序:3 4 8 6 7 5 2
此时又可以利用上面的结论划分了:根节点是2,然后根据2在中序中的位置可以划分为: -
序列 前序: 2 [3 4 5 6 8 7] 中序:[3 4 8 6 7 5 ] 2 -
此时树的结构为:
-
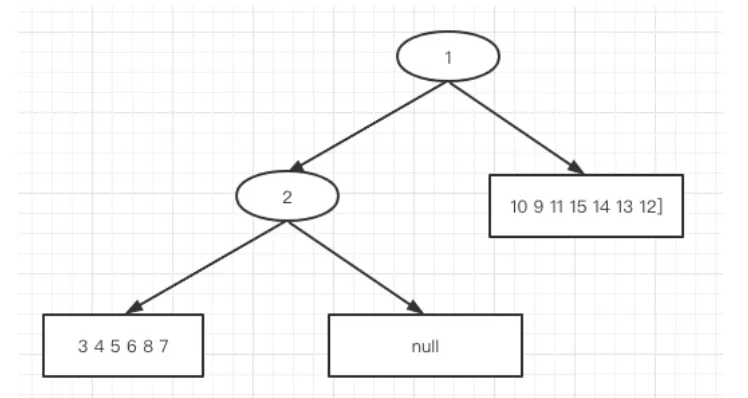
-
第三轮: -
对 3 4 5 6 8 7 继续划分 : 前序:3 [4 5 6 8 7] 中序:3 [ 4 8 6 7 5 ] 此时结构为:
-
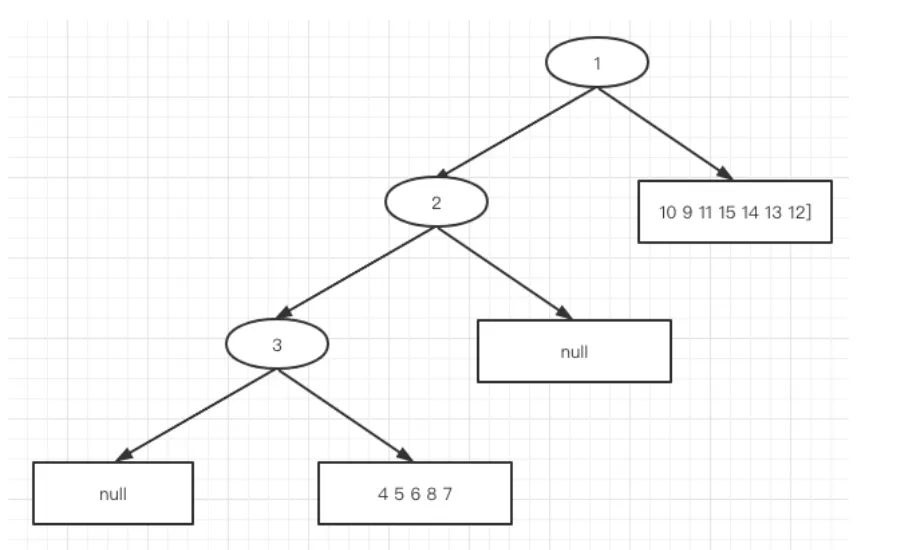
-
第四轮 -
对 4 5 6 8 7 继续划分:前序: 4 [5 6 8 7 ] 中序:4 [8 6 7 5 ]
-

-
第五轮: -
对 5 6 8 7 继续划分:前序:5 [6 8 7 ] 中序:[8 6 7] 5
-

-
同理,对序列 [10 9 11 15 13 14 12],进行划分:
-
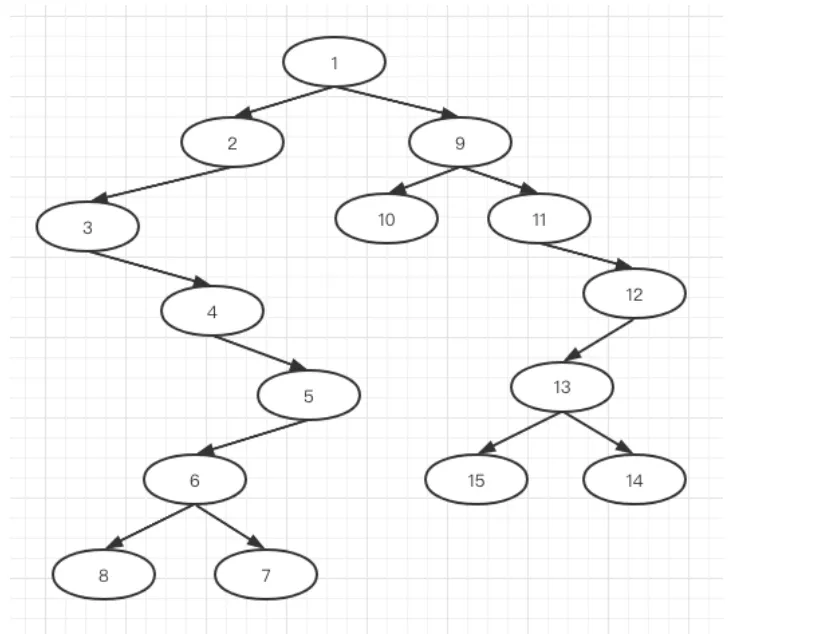
5.2 通过中序和后序序列恢复二叉树
- 通过中序和后序也能恢复原始序列的,唯一的不同是后序序列的最后一个是根节点,中序的处理也是上面一样的过程:
前序:12345687910 1112 1315 14
中序: 3486752110911 15 13 14 12
后序:876543210 15 14 13 12 1191
可以自行试一试,不再赘述。
问题:为什么前序和后序不能恢复二叉树
既然上面两种都行,那为什么前序和后序不行呢?我们看上面的例子:
(1) 前序: 123456879 10 1112 13 15 14
(2) 后序:87654321015 141312 1191
后序:876543210 15 14 13 12 1191
可以自行试一试,不再赘述。
问题:为什么前序和后序不能恢复二叉树
既然上面两种都行,那为什么前序和后序不行呢?我们看上面的例子:
(1) 前序: 123456879 10 1112 13 15 14
(2) 后序:87654321015 141312 1191 - 根据上面的说明,我们通过前序可以知道根节点是1,通过后序也能知道根节点是1,但是中间是怎么划分的呢?其他元素哪些属于左子树,哪些属于右子树呢?很明显通过两个序列都不知道,所以前序和后序序列不能恢复二叉树。
