快速幂----快速求解底数的n次幂
目录
一.快速幂
1.问题的引入
2.快速幂的介绍
3.核心思想
4.代码实现
2.猴子碰撞的方法数
1.题目描述
2.问题分析
3.代码实现
一.快速幂
1.问题的引入
问题:求解num的n次幂,结果需要求余
+7
对于这个问题我们可能就是直接调用函数pow(a,b)来直接求解a的b次幂问题,但是如果求解的结果很大,超过的double的数值范围,我们要求对最终的结果求余+7,我们如果直接调用pow()函数的话,求解出来的数已经超出了double的最大范围,根本无法求出,这个时候我们是否可以考虑在求解的过程中每一次的结果都求余
+7,而不是只在最终的结果求余
+7这样最终的结果肯定是小于
+7,一定不会超出最大的范围.
2.快速幂的介绍
快速幂:快速幂就是快速算底数的n次幂。其时间复杂度为 O(log₂N),与朴素的O(N)相比效率有了极大的提高。
3.核心思想
例如计算,10的二进制为1010,相当于求解
次方
=3*3*3*3*3*3*3*3*3*3
=(3*3)*(3*3*3*3*3*3*3*3)
=*
相当于我们每次对10的二进制的每一个位置求权(如果是二进制这个位是1),则乘以当前的叠加的数,
例如进行求余的步骤 :
定义变量ans保存的结果 1010位10的二进制表达方式
1010的第一位为0,这个时候num=num*num=; 二进制形式为:
1010的第二位为0,这个时候求权为1,ans=ans*num= num=num*num=
;二进制形式为:
1010的第三位为0,这个时候num=num*num=; 二进制形式为:
1010的第四位为1,这个时候求权为1,ans=ans*num=*
num=num*num=
;
4.代码实现
1.求余+7的版本,返回数据类型为int的结果
public int quickPow(long num,int n){long ans=1;long mod=1000000007;while(n!=0){if((n&1)==1)ans=(ans*num)%mod;num = num * num % mod;n>>=1;}return (int)(ans%mod);}2.不求余的版本,返回数据类型为long的结果
public long quickPow(long num,int n){long ans=1;while(n!=0){if((n&1)==1)ans=ans*num;num = num * num;n>>=1;}return ans;}
2.猴子碰撞的方法数
1.题目描述
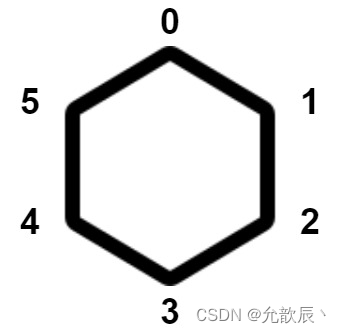
现在有一个正凸多边形,其上共有
n个顶点。顶点按顺时针方向从0到n - 1依次编号。每个顶点上 正好有一只猴子 。下图中是一个 6 个顶点的凸多边形。
每个猴子同时移动到相邻的顶点。顶点
i的相邻顶点可以是:
- 顺时针方向的顶点
(i + 1) % n,或- 逆时针方向的顶点
(i - 1 + n) % n。如果移动后至少有两个猴子位于同一顶点,则会发生 碰撞 。
返回猴子至少发生 一次碰撞 的移动方法数。由于答案可能非常大,请返回对
109+7取余后的结果。注意,每只猴子只能移动一次。
力扣: 力扣
2.问题分析
正难则反,题目问的是至少发生一次碰撞的移动次数,我们不妨把问题转换为求解猴子一次都不碰撞的次数,猴子一共有2的n次幂中跳跃的方式,求中有两种是一次都不碰撞的,一种是猴子全部顺时针进行跳跃,一种是猴子逆时针进行跳跃,所以猴子至少发生一次碰撞的次数=猴子总共的移动次数-2
3.代码实现
public int monkeyMove(int n) {long ans=1,a=2;long mod=1000000007;while(n!=0){if((n&1)==1)ans=(ans*a)%mod;a = a * a % mod;n>>=1;}return (int)((ans+mod-2)%mod);}