视觉SLAM十四讲ch6 非线性优化笔记
视觉SLAM十四讲ch6 非线性优化笔记
- 本讲目标
- 上讲回顾
- 状态估计问题
- 非线性最小二乘
- Gauss-Newton:高斯牛顿
- Levenburg-Marquadt:列文伯格-马夸尔特
- 小结
- 实践:CERES
- 实践:G2O
本讲目标
·理解最小二乘法的含义和处理方式。
·理解Gauss-Newton, Levenburg-Marquadt等下降策略。
·学习Ceres库和g2o库的基本使用方法。
上讲回顾

状态估计问题

运动方程运动噪声Wk,观测方程观测噪声Vk,j,Zk,j为像素。

滤波器求解状态估计:假设一个系统具有马尔科夫性,即一个系统下一个时刻的状态经受上一个时刻的状态。那就可以仅用维护当前时刻的状态,当有新的数据或者新的输入进入系统中,就可以更新当前状态的估计。只要关心当前时刻到下一个时刻估计。Xk,Yk怎样去维护他们就可以。

∝ :正比于的符号






非线性最小二乘





高斯牛顿 和 列文伯格-马夸尔特方法
Gauss-Newton:高斯牛顿


Levenburg-Marquadt:列文伯格-马夸尔特

p=1时,近似可靠。


H+λI相当于增加正定性。

H+λI:λI=0,只有二阶系数;H=0,只有一阶系数。
小结
- 非线性优化是个很大的主题,研究者们为之奋斗多年
- 主要方法:最速下降、牛顿、G-N、L-M、DogLeg等。
- 与线性规划不同,非线性需要针对具体问题具体分析。
- 问题非凸时,对初值敏感,会陷入局部最优
- 目前没有非凸问题的通用最优值的寻找办法
- 问题凸时,二阶方法通常一两步就能收敛
实践:CERES


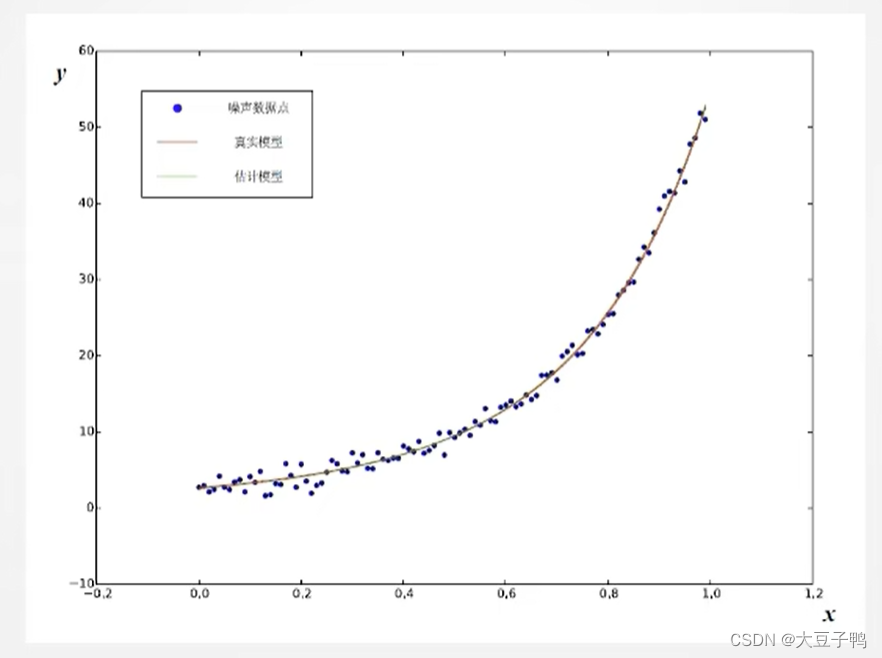
实践:G2O
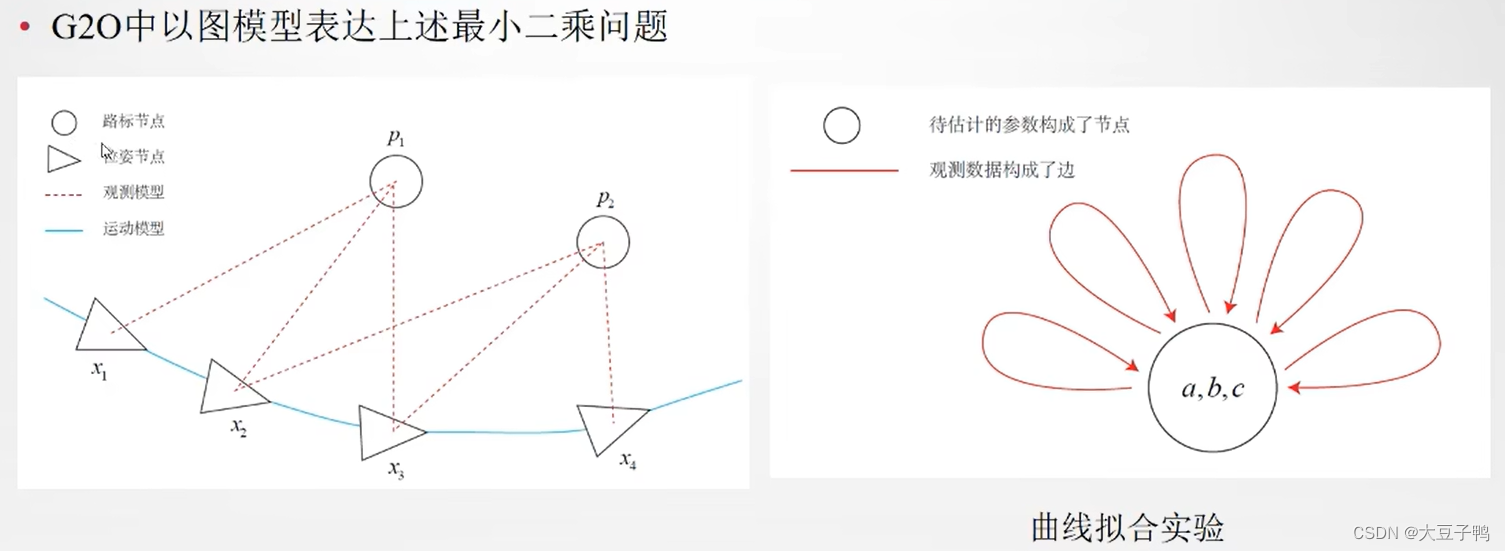
G-N有可能不收敛,L-M、DogLeg会收敛。
