C++ bfs再探迷宫游戏(五十五)【第二篇】
今天我们用bfs解决迷宫游戏。
1.再探迷宫游戏
前面我们已经接触过了迷宫游戏,并且学会了如何使用 DFS 来解决迷宫最短路问题。用 DFS 求解迷宫最短路有一个很大的缺点,需要枚举所有可能的路径,读入的地图一旦很大,可能的搜索方案数量会非常多,用 DFS 搜索显然效率会很低。
我们可以借助 BFS 来求解迷宫游戏。由于 BFS 是分层搜索,因此,第一次搜索到终点的时候,当前搜索的层数就是最短路径的长度。
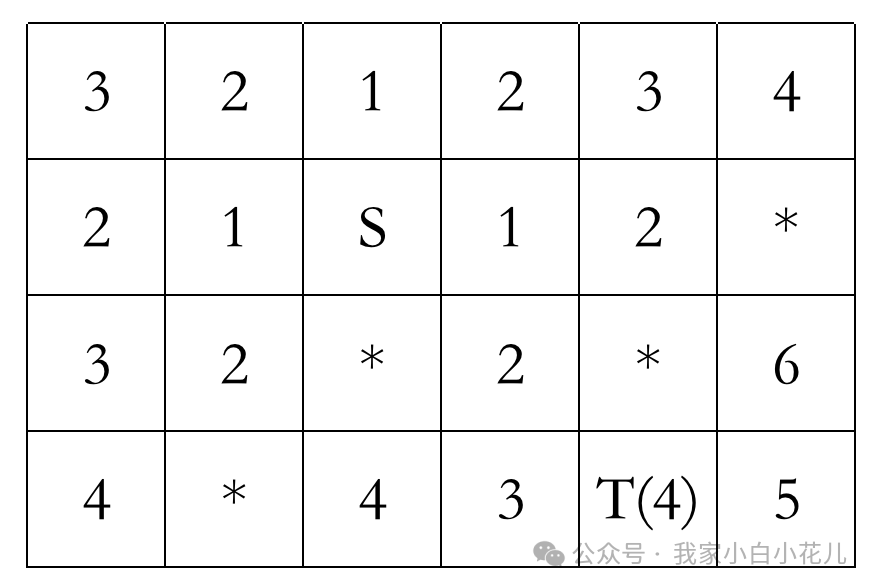
如果我们要求解起点到某个点的最短距离时,可以设置 int dis[maxn][maxn]; 记录起点到达每个点的最短距离。因为 bfs 搜索过程中第一次搜索到终点的时候是最短距离,所以可以让 dis 数组初始化为 −1−1,搜索过程中如果刚搜索到的点的 dis 等于 −1−1,表示这个点是第一次搜索到的点,需要更新 dis 数组。
程序:
#include <iostream>
#include <string>
#include <queue>
using namespace std;
int n, m;
string maze[110];
bool vis[110][110];
int dir[4][2] = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
bool in(int x, int y) {return 0 <= x && x < n && 0 <= y && y < m;
}
struct node {int x, y, d;node (int _x, int _y, int _d) {x = _x;y = _y;d = _d;}
};
int bfs (int sx, int sy){//从起点开始搜索queue <node> q;q.push(node (sx, sy, 0));vis[sx][sy] = true;//开始标记while (!q.empty()) {node now = q.front();//取出状态q.pop();//删除状态if (maze[now.x][now.y] == 'T') {return now.d;}for (int i = 0; i < 4; i++) {int tx = now.x + dir[i][0];int ty = now.y + dir[i][1];//横纵变化if (in(tx, ty) && maze[tx][ty] != '*' && !vis[tx][ty]) {//合法性判断vis[tx][ty] = true;q.push(node(tx, ty, now.d + 1));}}}return -1; //搜索失败
}
int main() {cin >> n >> m;for (int i = 0; i < n; i++) {cin >> maze[i];}int x, y;for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (maze[i][j] == 'S') {x = i;y = j;}}}cout << bfs(x, y) << endl;return 0;
}