力扣题目训练(8)
2024年2月1日力扣题目训练
- 2024年2月1日力扣题目训练
- 404. 左叶子之和
- 405. 数字转换为十六进制数
- 409. 最长回文串
- 116. 填充每个节点的下一个右侧节点指针
- 120. 三角形最小路径和
- 60. 排列序列
2024年2月1日力扣题目训练
2024年2月1日第八天编程训练,今天主要是进行一些题训练,包括简单题3道、中等题2道和困难题1道。惰性太强现在才完成,不过之后我会认真完成的。
404. 左叶子之和
链接: 左叶子之和
难度: 简单
题目:

运行示例:
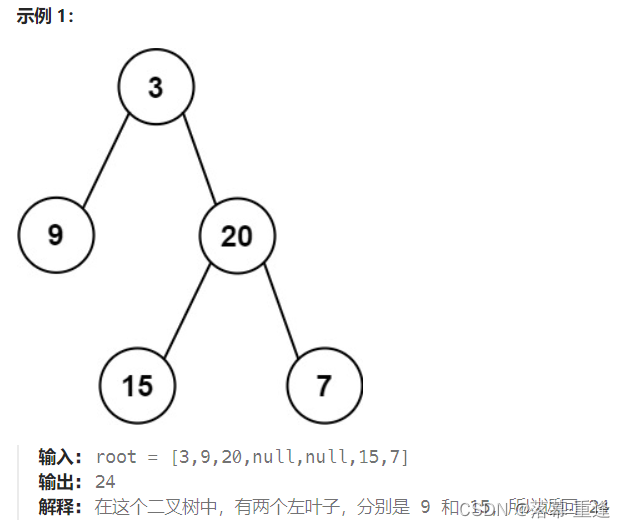
思路:
要求所有左叶子之和也就是通过遍历进行判断。
代码:
class Solution {
public:void preorder(TreeNode* root, int& res){if(root != NULL){if(root->left != NULL && root->left->left == NULL && root->left->right == NULL) res += root->left->val;preorder(root->left,res);preorder(root->right,res);}}int sumOfLeftLeaves(TreeNode* root) {int res = 0; preorder(root, res);return res;}
};
405. 数字转换为十六进制数
链接: 找不同
难度: 简单
题目:

运行示例:

思路:
这道题将给定的整数 转换为十六进制数,负整数使用补码运算方法。
在补码运算中,最高位表示符号位,符号位是 0 表示正整数和零,符号位是 1表示负整数。32位有符号整数的二进制数有 32 位,一位十六进制数对应四位二进制数,因此 32 位有符号整数的十六进制数有 8位。将 num 的二进制数按照四位一组分成 8组,依次将每一组转换为对应的十六进制数,即可得到 num的十六进制数。
假设二进制数的 8组从低位到高位依次是第 0组到第 7组,则对于第 i组,可以通过 (nums>>(4×i)) & 0xf得到该组的值,其取值范围是 0 到 15。
代码:
class Solution {
public:string toHex(int num) {if(num == 0) return "0";string res;for(int i = 7; i >= 0; i--){int val = (num >> (4 * i)) &0xf;if(res.size() > 0 || val > 0){char digit = val < 10 ?(char)('0'+val):(char)('a'+val-10);res += digit;}}return res;}
};
409. 最长回文串
链接: 最长回文串
难度: 简单
题目:

运行示例:

思路:
这道题本质就是计数看字母能不能组成回文数,若为偶数则可以,若为奇数则只有一个能组成,其余的需要减去1变为偶数才能构成回文数。
代码:
class Solution {
public:int longestPalindrome(string s) {bool flag = false;int ans = 0;unordered_map<char,int> temp;for(int i = 0; i < s.size(); i++){temp[s[i]]++;}for (auto p : temp){int value = p.second; if(value % 2 != 0){ans += value-1;if(flag == false){flag = true;ans++;} }else{ans += value;}}return ans;}
};
116. 填充每个节点的下一个右侧节点指针
链接: 填充节点
难度: 中等
题目:
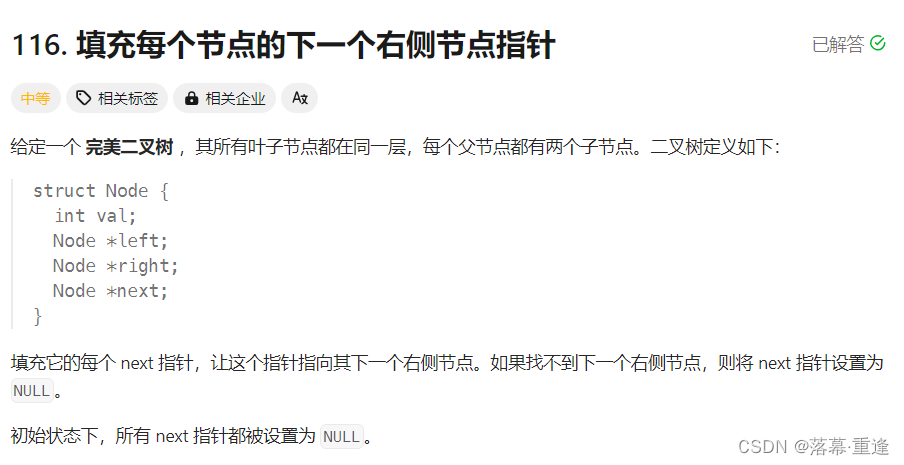
运行示例:
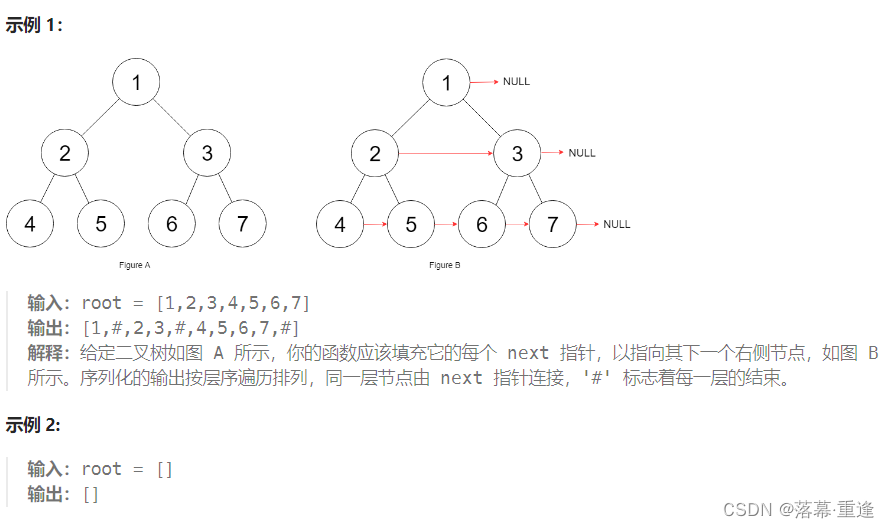
思路:
这道题可以看出是使用层次遍历来完成,故利用队列完成。
代码:
class Solution {
public:Node* connect(Node* root) {if(root == NULL) return NULL;queue<Node*> Q;Q.push(root);while(!Q.empty()){int size = Q.size();for(int i = 0; i < size; i++){Node* curr = Q.front();Q.pop();if(i == size-1){curr->next = NULL;}else{curr->next = Q.front();}if(curr->left != NULL) Q.push(curr->left);if(curr->right != NULL) Q.push(curr->right);}}return root;}
};
120. 三角形最小路径和
链接: 路径和
难度: 中等
题目:

运行示例:

思路:
可以看出这个题是需要利用动态规划解决,f[i][j]=min(f[i−1][j−1],f[i−1][j])+c[i][j]
代码:
class Solution {
public:int minimumTotal(vector<vector<int>>& triangle) {int n = triangle.size();vector<vector<int>> temp(n,vector<int>(n));temp[0][0] = triangle[0][0];for(int i = 1; i < n; i++){temp[i][0] = temp[i-1][0]+triangle[i][0];for(int j = 1; j < i; j++){temp[i][j] = min(temp[i-1][j],temp[i-1][j-1]) + triangle[i][j];}temp[i][i] = temp[i-1][i-1] + triangle[i][i];}return *min_element(temp[n-1].begin(),temp[n-1].end());}
};
60. 排列序列
链接: 排列序列
难度: 困难
题目:

运行示例:

思路:
可以通过观察发现对于 n 个不同的元素(例如数 1,2,⋯ ,n),它们可以组成的排列总数目为 n!。
对于给定的 n 和 k,我们不妨从左往右确定第 k 个排列中的每一个位置上的元素到底是什么。
我们首先确定排列中的首个元素 a1。根据上述的结论,我们可以知道:
以 1为 a1的排列一共有 (n−1)! 个;
以 2为 a1的排列一共有 (n−1)!个;
⋯⋯
以 n 为 a1的排列一共有 (n−1)! 个。
由于我们需要求出从小到大的第 k个排列,因此:
如果 k≤(n−1)!,我们就可以确定排列的首个元素为 1;
如果 (n−1)!<k≤2⋅(n−1)!,我们就可以确定排列的首个元素为 2;
⋯⋯
如果 (n−1)⋅(n−1)!<k≤n⋅(n−1)!,我们就可以确定排列的首个元素为 n。
可以利用这个发现解决问题。
代码:
class Solution {
public:int total(int n){if (n == 0 || n == 1) { return 1; } else { return n * total(n - 1); } }string getPermutation(int n, int k) {string ans = "";vector<int> temp;for(int i = 0; i < n; i++){temp.push_back(i+1);}while(k != 1){int count = (k%total(n-1) == 0)? k/total(n-1) -1:k/total(n-1);int s = temp[count];temp.erase(temp.begin() + count); ans += to_string(s);k -= count* total(n-1);n = n-1;}for(int i =0 ; i < temp.size(); i++){ans += to_string(temp[i]);}return ans;}
};
