7机器人位姿的数学描述与坐标变
由上次刚体的空间转动直接切换为机器人相关术语。
1.机器人位姿的数学描述与坐标变换
1.1位姿描述
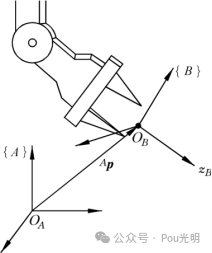
{B}相对于{A}的姿态描述用3x3矩阵表示为:
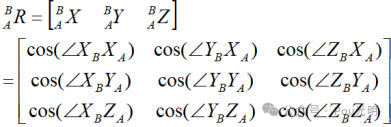
式中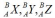 为三个单位正交主矢量,分别表示刚体坐标系{B}的三个坐标轴XBYBZB在参考系{A}中的方位,∠XBXA表示坐标轴XB与坐标轴XA之间的夹角,其他的类似。
为三个单位正交主矢量,分别表示刚体坐标系{B}的三个坐标轴XBYBZB在参考系{A}中的方位,∠XBXA表示坐标轴XB与坐标轴XA之间的夹角,其他的类似。
姿态矩阵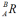 具有如下特点:
具有如下特点:
1>共有9个元素,但只有3个是独立的,有6个约束条件:
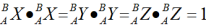
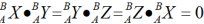
2>是单位正交阵,具有如下特点:
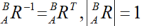
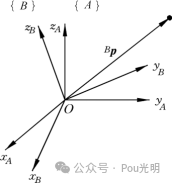
1.2 坐标系旋转(原点相同)
空间中任意点P在不同坐标系中的描述是不同的。为了阐明从一个坐标系描述到另一个坐标系描述的关系,需要讨论这种变换的数学问题。
设坐标系{B}与{A}有共同的坐标原点,但两者的方位不同,如图所示。用旋转矩阵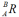 描述{B}相对于{A}的方位。同一点p在两个坐标系{A}和{B}中的描述PA和PB具有如下变换关系:
描述{B}相对于{A}的方位。同一点p在两个坐标系{A}和{B}中的描述PA和PB具有如下变换关系:
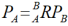
其中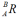 表示坐标系{B}相对于{A}的姿态,这里称其为旋转变换矩阵,简称旋转矩阵。旋转矩阵具有与姿态矩阵相同的特性:
表示坐标系{B}相对于{A}的姿态,这里称其为旋转变换矩阵,简称旋转矩阵。旋转矩阵具有与姿态矩阵相同的特性:
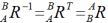
1.3坐标系绕单个坐标轴旋转的旋转矩阵
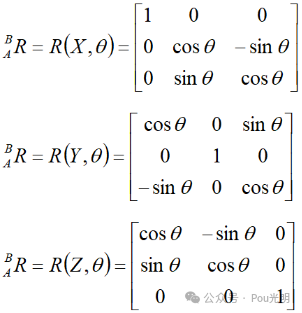
1.4 坐标系绕多个坐标轴转动的旋转矩阵
可分为绕动坐标系的多个坐标轴旋转和绕定坐标系的多个坐标轴旋转两类问题。
1.4.1绕动坐标系的多个坐标轴旋转的旋转矩阵
直接上结论,不推了。
坐标系{A}绕其Z轴旋转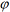 角,得到新坐标系{1},坐标系{1}再绕其Y轴旋转
角,得到新坐标系{1},坐标系{1}再绕其Y轴旋转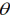 角,得到新坐标系{2},坐标系{2}再绕其Z轴旋
角,得到新坐标系{2},坐标系{2}再绕其Z轴旋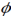 转角,得到新坐标系{B},求旋转矩阵
转角,得到新坐标系{B},求旋转矩阵
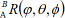 .
.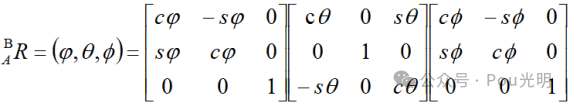
结论:旋转矩阵等于绕三个坐标轴转动的旋转矩阵的顺序乘积。
1.4.2绕定坐标系的多个坐标轴旋转的旋转矩阵
坐标系{A}绕其Z轴旋转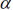 角,得到新坐标系{m},坐标系{m}再绕坐标系{A}的Z轴旋转
角,得到新坐标系{m},坐标系{m}再绕坐标系{A}的Z轴旋转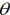 角,得到新坐标系{B},求旋转矩阵
角,得到新坐标系{B},求旋转矩阵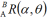 .
.
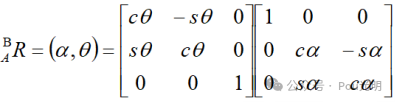
结论:绕着固定坐标系{A}的两个坐标轴X、Z转动的旋转矩阵等于绕Z轴和绕X轴转动的两个旋转矩阵的乘积。
欢迎关注!
了解更多学习笔记!

