P3647 题解
文章目录
- P3647 题解
- Overview
- Description
- Solution
- Lemma
- Proof
- Main
- Code
P3647 题解
Overview
很好的题,但是难度较大。
模拟小数据!——【数据删除】
Description
给定一颗树,有边权,已知这棵树是由这两个操作得到的:
Append(u, w):在 u u u 和 w w w 之间连一条红边,注意这里的 w w w 必须是新点。Insert(u, v, w):在 u u u 和 w w w, v v v 和 w w w 之间各连一条蓝边,注意这里的 w w w 必须是新点。
问蓝线的长度最大能到多少。
Solution
我们可以尝试将所有的 Insert 所产生的蓝边对都提取出来。
它们只可能有两种形式:son - u - father 和 son1 - u - son2。
Lemma
引理:所有的蓝边都可以在某一个根上表现出形如 son - u - father 的形式。
Proof
当树上没有形如 son1 - u - son2 的蓝边时,显然成立;
当树上恰好有一个形如 son1 - u - son2 的蓝边时,可以将 son1 和 son2 其中之一作为根,解决问题;
当树上有大于一个形如 son1 - u - son2 的蓝边时,可以证明不存在这样的边。
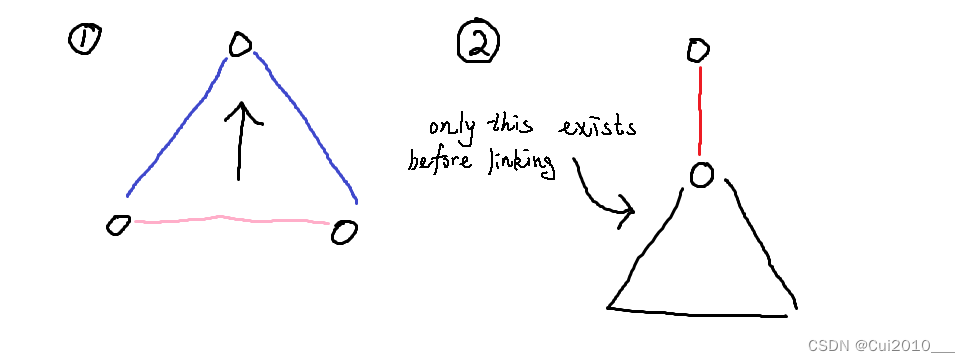
如图,当存在形如 1 的情况时,son1 和 son2 构成了单独的连通块,因为如果不是,那么 son1 和 son2 一定会是父子关系,矛盾;
当存在多个这样的连通块时,如图 2,建树时节点一定会组成单一的连通块,因为 u u u 总是存在,所以不成立。
Main
有了引理,就可以树形 dp 了。
枚举树根,对每个根 DP。设 d u , 0 / 1 d_{u,0/1} du,0/1 为 u u u 为根, u u u 是否为蓝边终点的子树最大边权和。
先看 d u , 0 d_{u,0} du,0,因为没有边上的限制,所以可以任意取,对于是中点的情况,可以再加上边权 w ( u , v ) w(u,v) w(u,v),即 max ( d v , 1 + w ( u , v ) , d v , 0 ) \max(d_{v,1}+w(u,v), d_{v,0}) max(dv,1+w(u,v),dv,0)。
再看 d u , 1 d_{u,1} du,1,一定有一个 d v , 0 + w ( u , v ) d_{v,0}+w(u,v) dv,0+w(u,v),其它都是 max ( d v , 1 + w ( u , v ) , d v , 0 ) \max(d_{v,1}+w(u,v), d_{v,0}) max(dv,1+w(u,v),dv,0),所以要加上 max Δ sum \max \Delta_{\text{sum}} maxΔsum。
所以关于 d d d 的状态转移方程可以这样写:
d u , 0 = ∑ v ∈ son ( u ) max ( d v , 1 + w ( u , v ) , d v , 0 ) d u , 1 = d u , 0 + max v ∈ son ( u ) { d v , 0 + w ( u , v ) − max ( d v , 1 + w ( u , v ) , d v , 0 ) } d_{u,0} = \sum_{v\in \text{son}(u)}\max(d_{v,1}+w(u,v),d_{v,0})\\d_{u,1} = d_{u,0}+\max_{v\in \text{son}(u)}\{d_{v,0} + w(u,v) - \max(d_{v,1} + w(u,v), d_{v,0})\} du,0=v∈son(u)∑max(dv,1+w(u,v),dv,0)du,1=du,0+v∈son(u)max{dv,0+w(u,v)−max(dv,1+w(u,v),dv,0)}
这样,就可以枚举根得到 O ( n 2 ) O(n^2) O(n2) 的复杂度, 15 pts 15\text{pts} 15pts。
接下来考虑换根 DP。
一张图解释接下来两个 DP 数组的含义。
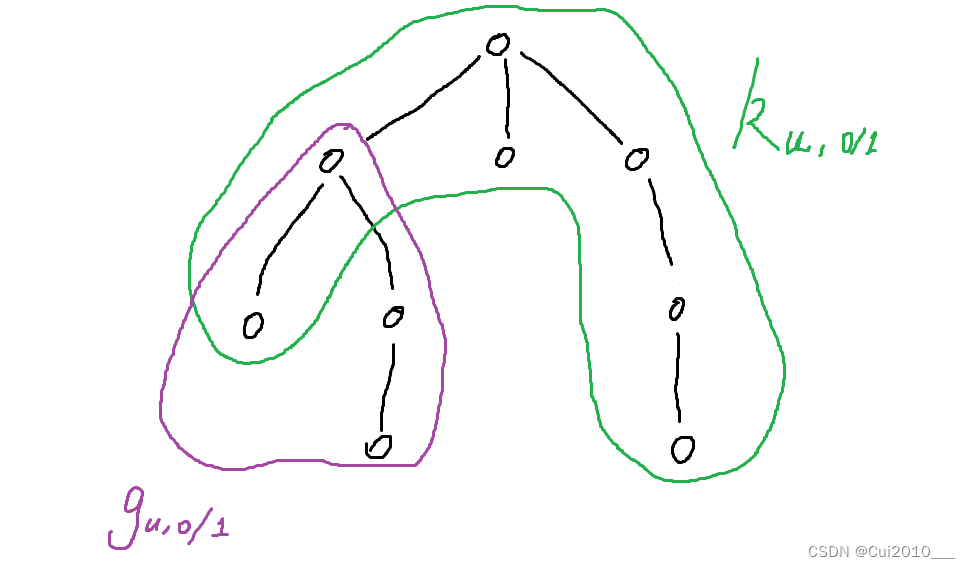
这里的 g g g 并不描述这个子树,而是以 u u u 为根的整棵树。
根据 f f f 的转移方程,我们照样也可以推出 g g g 和 k k k 的转移方程,留给读者思考。
注意到方程里仍有大量之前可以利用的内容,所以需要维护最大值和次大值。
Code
#include <bits/stdc++.h>using namespace std;int dp[200001][2], dp1[200001][2], dp2[200001][2], mx[200001], mx2[200001];vector<pair<int, int> > gv[200001];inline void add_edge(int u, int v, int w){gv[u].push_back(make_pair(v, w));gv[v].push_back(make_pair(u, w));
}void dfs(int u, int fa){vector<int> vec;vec.push_back(INT_MIN), vec.push_back(INT_MIN);for(auto v : gv[u]){if(v.first == fa) continue;dfs(v.first, u);dp[u][0] += max(dp[v.first][0], dp[v.first][1] + v.second);vec.push_back(dp[v.first][0] + v.second - max(dp[v.first][0], dp[v.first][1] + v.second));}sort(vec.begin(), vec.end(), greater<int>());mx[u] = vec[0], mx2[u] = vec[1];dp[u][1] = dp[u][0] + mx[u];
}void dfs1(int u, int fa, int lst){for(auto v : gv[u]){if(v.first == fa) continue;int tmp = dp[v.first][0] + v.second - max(dp[v.first][0], dp[v.first][1] + v.second);dp2[u][0] = dp1[u][0] - max(dp[v.first][0], dp[v.first][1] + v.second);dp2[u][1] = dp2[u][0] + (mx[u] == tmp ? mx2[u] : mx[u]);if(fa + 1) dp2[u][1] = max(dp2[u][1], dp2[u][0] + dp2[fa][0] + lst - max(dp2[fa][0], dp2[fa][1] + lst));dp1[v.first][0] = dp[v.first][0] + max(dp2[u][0], dp2[u][1] + v.second);
// dp1[v.first][1] = dp1[v.first][0] + max(mx[v.first], dp2[u][0] + v.second - max(dp2[u][0], dp2[u][1] + v.second));dfs1(v.first, u, v.second);}
}void init_vars(){// type your initiating code...
}void solve(int testcase, ...){init_vars();int n; cin >> n;for(int i = 0; i < n - 1; i++){int u, v, w; cin >> u >> v >> w;add_edge(u, v, w);}dfs(1, -1); dp1[1][0] = dp[1][0];dfs1(1, -1, 0);int ans = 0;for(int i = 1; i <= n; i++){//cout << mx[i] << " " << mx2[i] << endl;ans = max(ans, dp1[i][0]);}cout << ans << endl;
}signed main(){
#ifdef filesfreopen(".in", "r", stdin);freopen(".out", "w", stdout);
#endifios::sync_with_stdio(0);cin.tie(0), cout.tie(0);solve(1);
#ifdef filesfclose(stdin); fclose(stdout);
#endifreturn 0;
}/** things to check* 1. int overflow or long long memory need* 2. recursion/array/binary search/dp/loop bounds* 3. precision* 4. special cases(n=1,bounds)* 5. delete debug statements* 6. initialize(especially multi-tests)* 7. = or == , n or m ,++ or -- , i or j , > or >= , < or <=* 8. keep it simple and stupid* 9. do not delete, use // instead* 10. operator priority* 11. is there anything extra to output?* 12. THINK TWICE CODE ONCE, THINK ONCE DEBUG FOREVER* 13. submit ONCE, AC once. submit twice, WA forever* 14. calm down and you'll get good rank* 15. even a bit wrong scores zero* 16. ...**//** something to think about* 1. greedy? dp? searching? dp with matrix/ segment tree? binary search? ...?* 2. If it is difficult, why not the opposite?**//*########## ############ ##### ######### ##### #### ####
#### ##### #### ####
#### ########## #### ####
#### ##### #####
#### ##### ######### ##### ################ ############# #####
*/