力扣70. 爬楼梯(动态规划 Java,C++解法)
Problem: 70. 爬楼梯
文章目录
- 题目描述
- 思路
- 解题方法
- 复杂度
- Code
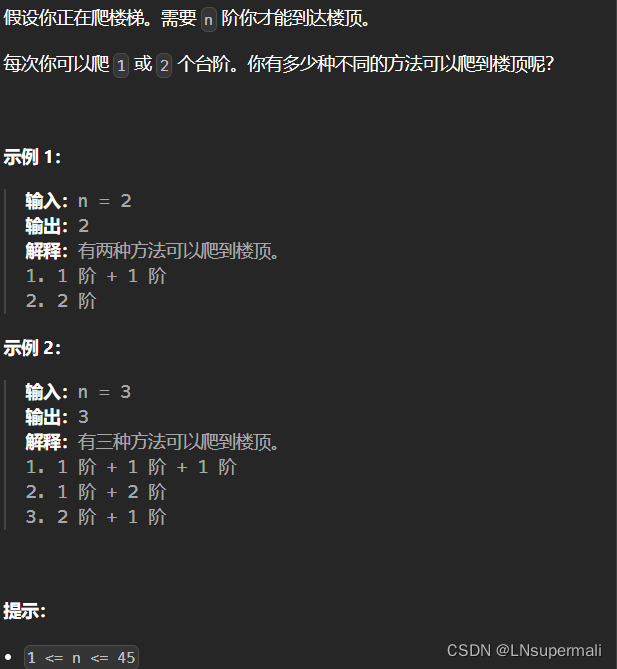
题目描述
思路
由于本题目中第i层台阶只能由于第i- 1层台阶和第i-2层台阶走来,所以可以联想到动态规划,具体如下:
1.定义多阶段决策模型:对于每一上台阶看作一种状态;
2.定义状态转移方程:int[] dp = new int[n + 1]用于记录第i个台阶可以走到的走法;dp[i] = dp[i - 1] + dp[i - 2];
解题方法
1.定义数组int[] dp = new int[n + 1]用于记录第i个台阶可以走到的走法
2.初始化dp[1] = 1; dp[2] = 2;
3.从dp数组下标为3处开始完成动态转移方程;
4.返回dp[n]
复杂度
时间复杂度:
O ( n ) O(n) O(n);其中 n n n为台阶数
空间复杂度:
O ( n ) O(n) O(n)
Code
class Solution {/*** Dynamic programing* @param n The number of stage* @return int*/public int climbStairs(int n) {if (n <= 2) {return n;}//Record how many moves there are on step iint[] dp = new int[n + 1];dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; ++i) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
}
class Solution {
public:int climbStairs(int n) {if (n <= 2) {return n;}vector<int> dp(n + 1);dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; ++i) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
};