希尔(Shell)排序
文章目录
- 希尔排序的基本思想
- 本质
- 增量(间隔)的选取
- 希尔排序的时间复杂度
- 希尔排序代码实现
- 希尔排序的稳定性
希尔排序的基本思想
将要排序的序列按一定间隔(增量)分组,将每一组的数据按插入排序进行排序,再缩小间隔,再分组,再将每一组的数据按插入排序进行排序,直到间隔为1时整个序列为一组
而插入排序就是将就相邻(间隔为1)的数据比较进而排序,所以间隔为1时就是插入排序
例:
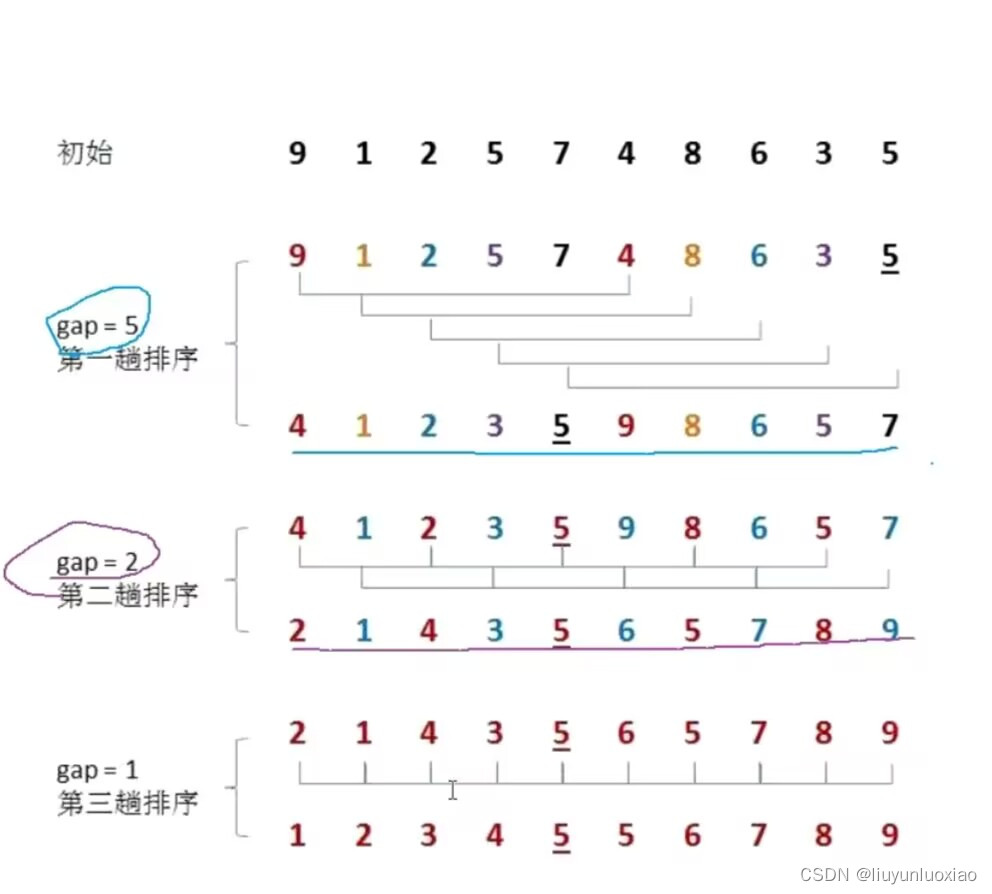
一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
本质
希尔排序算法是直接插入排序算法的一种改进,减少了其复制的次数,速度要快很多。
原因是,当n值很大时数据项每一趟排序需要移动的个数很少,但数据项的距离很长。当n值减小时每一趟需要移动的数据增多,此时已经接近于它们排序后的最终位置。 正是这两种情况的结合才使希尔排序效率比插入排序高很多
一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
增量(间隔)的选取
希尔排序的性能与所选取的增量(间隔)大小有很大关系
但是最优的增量(间隔)选取与序列数据之间的关系至今还是难题
不过一般使希尔排序增量的选取是要排序序列数据个数除以2,直到增量为1.
一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
希尔排序的时间复杂度
希尔排序的时间的时间复杂度为O(N^1.5),希尔排序时间复杂度的下界是
O(N*logN)
所以希尔排序没有快速排序/堆排序等那那么快[O(N*logN)],但是希尔排序在中等大小规模表现较好,对规模非常大的数据排序不是最优选
一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
希尔排序代码实现
希尔排序代码实现其实很简单,就是把直接插入的代码中的增量1,全部换成变化的增量,
然后再在外面套一个增量变化的循环,就可以了。


与插入排序的代码比较

一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
希尔排序代码
void ShellSort(int a[], int n)
{//gap是间隔(增量)int gap = n;while (gap > 1){gap /= 2;//间隔(增量)每次循环都缩小一半//end表示 每一组 有序序列最末尾的元素的下标int end = 0;//tmp表示 每一组 无序序列的第一个元素的下标int tmp = 0;int i = 0;//把插入排序中的1都换成gapfor (i = 0; i < n - gap; i++){end = i;tmp = a[end + gap];while (end >= 0)//end{//如果前gap个元素大于后gap个,就让前gap个向后移gap位//给后gap个可插入的空隙if (a[end] > tmp){a[end + gap] = a[end];end-=gap;}else{ //因为是从已经有序的序列的末尾向前插入//所以前一个之前的元素都比它小,所以不用再比较,直接结束循环break;}}//插入空出的空隙a[end + gap] = tmp;}}
}
一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
希尔排序的稳定性
希尔排序根据增量不同,分组不同,相等的元素可能会被分到不同的组,进而可能在不同的插入排序过程中相等的元素的相对位置改变。
所以希尔排序是不稳定的
