当前位置：首页 > news >正文

电子技术——CMOS反相器

news 2025/8/5 15:39:53

电子技术——CMOS反相器

Logo

在本节，我们深入学习CMOS反相器。

电路原理

下图是我们要研究的CMOS反相器的原理图：

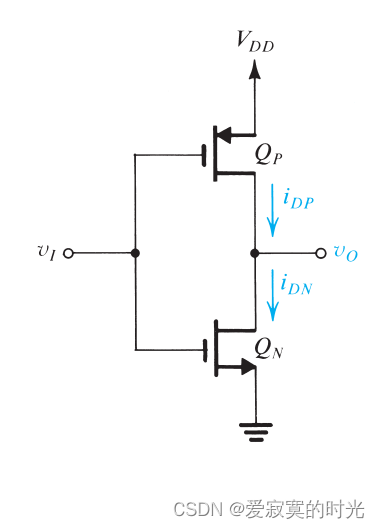
CMOS反相器
下图展示了当输入 $v_I = V_{DD}$ 时的 $i_D-v_{DS}$ 曲线：

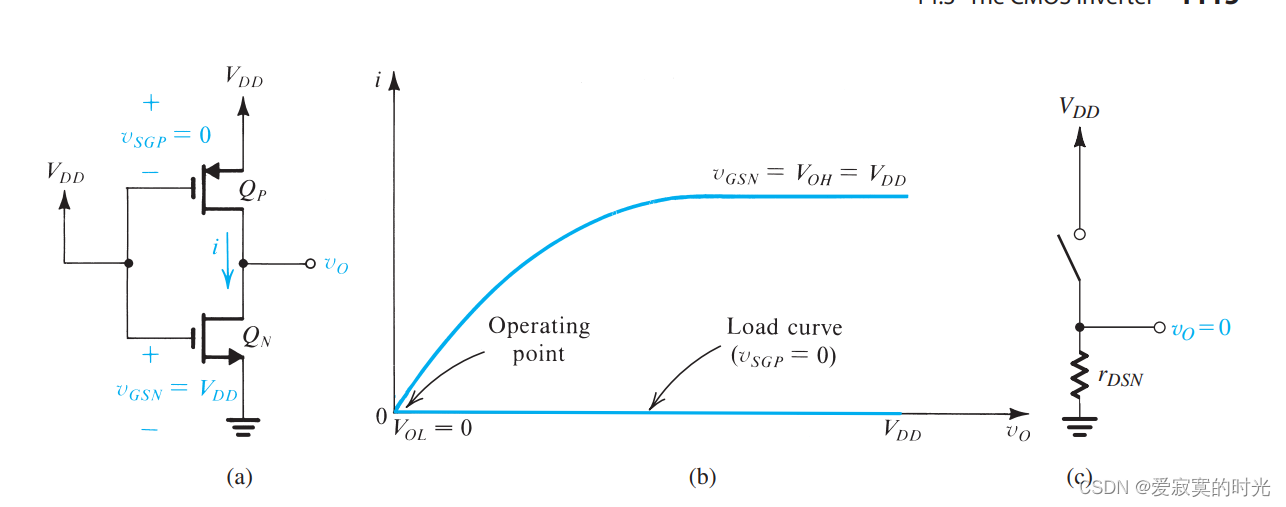
CMOS反相器曲线
我们把 $Q_N$ 当做是驱动源，而 $Q_P$ 作为负载，我们在图像上叠加关于 $Q_P$ 在 $v_{SGP} = 0$ 的负载曲线。因为 $v_{SGP} < |V_t|$ 因此负载曲线是一条零电流的水平直线。两个曲线的交点就是我们的工作点，我们发现此时电流为零，输出电压为零。同样意味着此时耗散功率为零。然而，工作点处在曲线 $i_D-v_{DS}$ 的上升处，具有有限的斜率，因此 $Q_N$ 对外表现出有限的阻抗，如图©：

$rDSN=1/[kn′(WL)n(VDD−Vtn)]r_{DSN} = 1 / [k_n'(\frac{W}{L})_n (V_{DD} - V_{tn})]$

另外一种情况，当输入 $v_I = 0$ 的时候，如图：

CMOS反相器曲线
因为 $v_{GSN} = 0$ 此时驱动曲线是一条零电流的直线，此时负载曲线是 $v_{SGP} = V_{DD}$ 的曲线。我们发现，此时交点在零电流，输出电压为 $v_O = V_{DD}$ 。耗散功率为零。同样的， $Q_P$ 表现出有限的阻抗：

$rDSP=1/[kp′(WL)p(VDD−∣Vtp∣)]r_{DSP} = 1 / [k_p' (\frac{W}{L})_p (V_{DD} - |V_{tp}|)]$

虽然，静态电流为零，这种CMOS反相器可以提供较大的负载能力。例如，负载是容性负载的时候，当 $Q_N$ 导通的时候，由于其较小的开关阻抗，可以提供一个较短的对地回路，可以使得容性负载迅速泄放电荷，拉低电位，因此 $Q_N$ 称为下拉元件。同样的，当 $Q_P$ 导通的时候，由于其较小的开关阻抗，可以提供一个较短的对电压通路，可以使得容性负载迅速充满电荷，拉高电位，因此 $Q_P$ 称为上拉元件。

根据上面的讨论CMOS反相器作为理想的反相器：

输出电压的范围在 $0-V_{DD}$ 电压压摆达到最大。同时，两个MOS可以进行匹配使得提供一个对称的电压传导特性，具有较宽的噪声容限。
静态功率为零，这是因为电压源和地直接没有直接的DC回路。
对地和电压都是低阻抗路径，较低的输出阻抗使得反相器具有较高的驱动能力，以及实现电气功能与元件参数无关，提高噪声和其他干扰的容忍性。
上拉的下拉元件使得电路的翻转速度更快，对于容性负载具有较高的驱动能力。
输入阻抗为无穷大。所以CMOS反相器可以驱动大量同样的CMOS反相器而不造成电压水平损失。当然，增加被驱动元件的数量就意味着增加了容性负载，这会降低电平的翻转速度。

电压传导特性

通过联立两个曲线，我们可以绘制出CMOS反相器的电压传导特性曲线，这里给出驱动和负载方程：

$iDN=kn′(WL)n[(vI−Vtn)vO−12vO2],vO≤vI−Vtni_{DN} = k_n'(\frac{W}{L})_n [(v_I - V_{tn})v_O - \frac{1}{2}v_O^2], v_O \le v_I - V_{tn}$

$iDN=12kn′(WL)n(vI−Vtn)2,vO≥vI−Vtni_{DN} = \frac{1}{2}k_n' (\frac{W}{L})_n (v_I - V_{tn})^2, v_O \ge v_I - V_{tn}$

$iDP=kp′(WL)p[(VDD−vI−∣Vtp∣)(VDD−vO)−12(VDD−vO)2],vO≥vI+∣Vtp∣i_{DP} = k_p' (\frac{W}{L})_p [(V_{DD} - v_I - |V_{tp}|)(V_{DD} - v_O) - \frac{1}{2}(V_{DD} - v_O)^2], v_O \ge v_I + |V_{tp}|$

$iDP=12kp′(WL)p(VDD−vI−∣Vtp∣)2,vO≤vI+∣Vtp∣i_{DP} = \frac{1}{2} k_p' (\frac{W}{L})_p(V_{DD} - v_I - |V_{tp}|)^2, v_O \le v_I + |V_{tp}|$

通常电路设计者通常将阈值电压设计为 $V_{tn} = |V_{tp}| = V_t$ 。同样，尽管并不总是这样，我们也假设两个MOS完全匹配，即 $k_n'(W/L)_n = k_p'(W/L)_p$ 。因为存在电子速率差异，当两个MOS具有相同的长度的时候，其宽度满足：

$WpWn=μnμp\frac{W_p}{W_n} = \frac{\mu_n}{\mu_p}$

此时电路具有对称的传递特性，以及相同的负载驱动能力。电压传导特性如图：

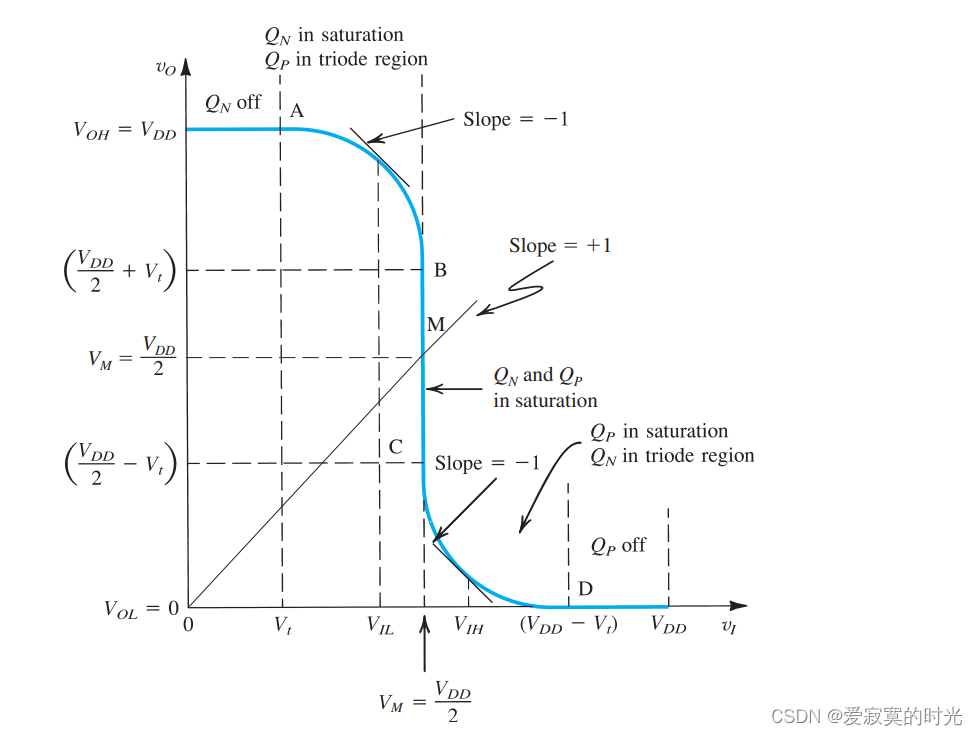
电压传导特性

其中BC段为MOS的放大器区，因为我们忽略了沟道宽度调制效应，因此在BC端具有无限大的增益。由于电路的对称性，传导中点发生在 $V_M = V_{DD} / 2$ 的地方，上下边界点为 $v_O(B) = V_{DD} / 2 + V_t$ （ $Q_P$ 进入三极管区）以及 $v_O(C) = V_{DD} / 2 -V_t$ （ $Q_N$ 进入三极管区）。

为了决定点 $V_{IH}$ 的位置，我们注意到此时 $Q_N$ 进入三极管区，通过电流相等我们联立方程：

$(vI−Vt)vO−12vO2=12(VDD−vI−Vt)2(v_I - V_t)v_O - \frac{1}{2} v_O^2 = \frac{1}{2} (V_{DD} - v_I - V_t)^2$

对 $v_O$ 求导可得：

$(vI−Vt)dvOdvI+vO−vOdvOdvI=−(VDD−vI−Vt)(v_I - V_t) \frac{dv_O}{dv_I} + v_O - v_O \frac{dv_O}{dv_I} = -(V_{DD} - v_I - V_t)$

带入 $v_I = V_{IH}$ 以及 $dvOdvI=−1\frac{dv_O}{dv_I} = -1$ 我们得到：

$vO=VIH−VDD2v_O = V_{IH} - \frac{V_{DD}}{2}$

带入 $v_I = V_{IH}$ 得到 $v_O$ 带回上式得到：

$VIH=18(5VDD−2Vt)V_{IH} = \frac{1}{8} (5V_{DD} - 2V_t)$

同样的做法我们得到：

$VIL=18(3VDD+2Vt)V_{IL} = \frac{1}{8} (3V_{DD} + 2V_t)$

可以计算出噪声容限：

$NMH=VOH−VIH=18(3VDD+2Vt)NM_H = V_{OH} - V_{IH} = \frac{1}{8}(3V_{DD} + 2V_t)$

$NML=VIL−VOL=18(3VDD+2Vt)NM_L = V_{IL} - V_{OL} = \frac{1}{8}(3V_{DD} + 2V_t)$

正如期望的那样，若两个MOS完全一样，则此时传导特性完全对称。

MOS不完全匹配的情况

若我们想使得MOS完全匹配，那么PMOS器件的尺寸就要是NMOS尺寸的3到4倍。这会导致更大的硅区域。一方面浪费了一些硅区域，为器件小型化造成了不利条件，另一方面增加了器件的容性阻抗，增加了CMOS反相器的时间延迟。因此，通常情况下MOS是不完全匹配。

首先我们推导不完全匹配下的M点，因为两个MOS都工作在饱和区，因此带入 $v_I = v_O = V_M$ 我们得到：

$VM=r(VDD−∣Vtp∣)+Vtnr+1V_M = \frac{r(V_{DD} - |V_{tp}|) + V_{tn}}{r + 1}$

这里：

$\sqrt{\frac{k_p}{k_n}} = \sqrt{\frac{\mu_p W_p}{\mu_n W_n}}$

这里我们让 $L$ 的长度相同，通常是在指定工艺下的最小精度值，注意到当MOS完全匹配的时候，此时 $r = 1$ 。对于 $V_{tp}| = V_{tn}$ 并且 $r = 1$ 产生 $V_M = V_{DD} / 2$ 。对于给定 $V_{DD}$ 和 $V_{tn}$ 以及 $V_{tp}$ 则 $V_M$ 是一个和工艺参数 $r$ 相关的函数。例如，在0.18um工艺下：