计算机图形学作业:三维线段的图形变换
1. 将三维空间某线段 P1P2进行如下的操作,请按要求回答问题:
(1) 沿 X 轴、Y 轴和 Z 轴分别平移 dx、dy 和 dz 的长度,给出相应的变换矩阵。
变换矩阵为:
T=100001000010dxdydz1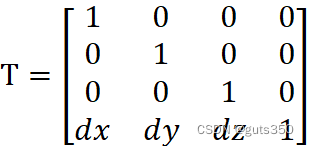
(2) 绕 X 轴旋转 alpha 度角,绕 Y 轴旋转 Beta 度角,绕 Z轴旋转 theta 度角,给出相应的变换矩阵。
变换矩阵(逆时针旋转)为:
T=10000cosαsinα00-sinαcosα00001 cosβ0-sinβ00100sinβ0cosβ00001cosθsinθ00-sinθcosθ0000100001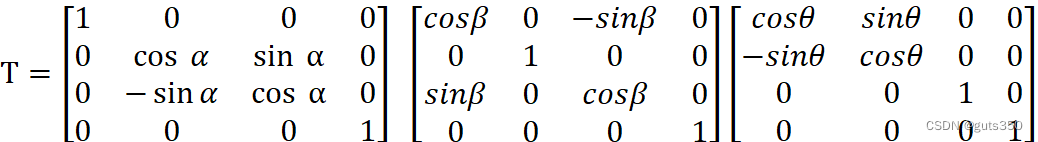
(3) 在保持 P1 点位置不变的情况下,将线段放大 s 倍,给出相应的变换矩阵。
设P1 点坐标为(x1,y1,z1)
变换矩阵为:
T=100001000010-x1-y1-z11 s0000s0000s00001100001000010x1y1z11
4) 依次完成(1)(2)(3)步的操作,给出相应的变换矩阵。
首先,沿 X 轴、Y 轴和 Z 轴分别平移 dx、dy 和 dz 的长度(设P1 点坐标为(x1,y1,z1)):
T=100001000010dxdydz1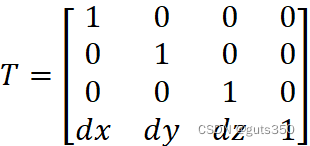
故
x'y'z'1=xyz1T![]()
然后,绕 X 轴旋转 alpha 度角,绕 Y 轴旋转 Beta 度角,绕 Z轴旋转 theta 度角:
令
R=10000cosαsinα00-sinαcosα00001 cosβ0-sinβ00100sinβ0cosβ00001cosθsinθ00-sinθcosθ0000100001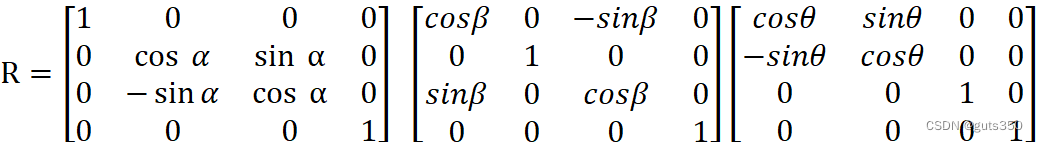
故
x''y''z''1=x'y'z'1R![]()
最后,保持 P1 点位置不变的情况下,将线段放大 s 倍,给出相应的变换矩阵:
设P1 点坐标此时为(x1’’,y1’’,z1’’),则
S=100001000010-x1''-y1''-z1''1 s0000s0000s00001100001000010x1''y1''z1''1
故
x'''y'''z'''1=x''y''z''1S![]()
(5) 以空间某线段 P3(x3,y3,z3)P4(x4,y4,z4)为轴旋转 alpha 度角,给出相应的变换矩阵。
1:平移旋转轴端点P3与坐标原点重合,相应变换矩阵为:
T=100001000010-x3-y3-z31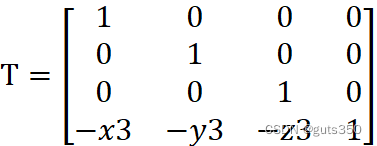
2:将旋转轴P3P4绕x轴逆时针旋转θ 度角使其落在xOz坐标平面上,然后绕y轴逆时针旋转β 度角使其与z轴重合,相应的变换矩阵为:
RXY=10000cosθsinθ00-sinθcosθ00001 cosβ0sinβ00100-sinβ0cosβ00001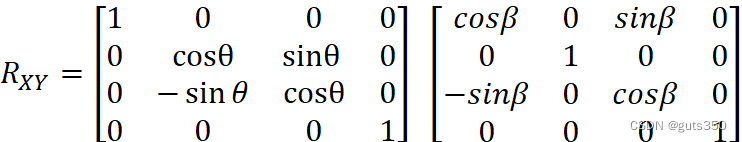
3:再绕z轴旋转α度角,相应的变换矩阵为:
RZ=cosαsinα00-sinαcosα0000100001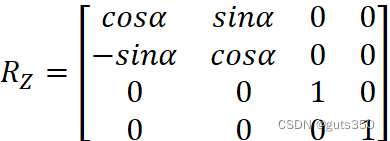
4:进行步骤2旋转变换的逆变换,相应的变换矩阵为:
RXY-1= cosβ0sinβ00100-sinβ0cosβ00001-110000cosθsinθ00-sinθcosθ00001-1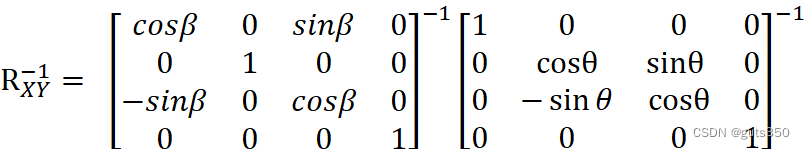
5:进行步骤1平移变换的逆变换,相应的变换矩阵为:
T'=100001000010x3y3z31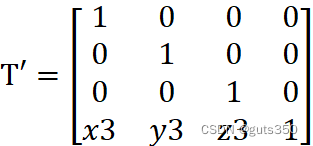
所以,以空间某线段 P3(x3,y3,z3)P4(x4,y4,z4)为轴旋转 alpha 度角,相应的变换矩阵为:
R=TRXYRZRXY-1T'![]()
