LeetCode 热题 HOT 100 Java 题解 -- Part 3
练习地址
Part 1 : https://blog.csdn.net/qq_41080854/article/details/128829494
Part 2 : https://blog.csdn.net/qq_41080854/article/details/129278336
LeetCode 热题 HOT 100 Java 题解 -- Part 3
- 76. 最佳买卖股票时机含冷冻期
- 77. 戳气球
- 78. 零钱兑换
- 79. 打家劫舍 III
- 80. 比特位计数
- 81. 前 K 个高频元素
- 82. 字符串解码
- 83. 除法求值
- 84. 根据身高重建队列
- 85. 分割等和子集
- 86. 路径总和 III
76. 最佳买卖股票时机含冷冻期
给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
解析
dp[i] 表示 第 i 天的最大收益,由两个状态决定dp[i] = Max(dp[i, 0],dp[i, 1]), dp[i, 0] 表示当天没有股票,dp[i, 1]表示当天有股票
dp[i, 0] = Max(dp[i - 1, 1] + price[i], dp[i - 1, 0]) 当天没有股票由今天卖的和昨天就没有决定,需要注意先有才能卖
dp[i, 1] = Max(dp[i - 2, 0] - price[i], dp[i - 1, 1]) 当天有股票由今天买的(有冷冻期限制)和昨天就有决定,需要注意先没有才能买
代码
class Solution {public int maxProfit(int[] prices) {if(prices == null || prices.length == 0) return 0;//dp[i][0] 第i天没有股票 dp[i][1] 第 i 天有股票int[][] dp = new int[prices.length][2];dp[0][0] = 0;dp[0][1] = -prices[0];for(int i = 1; i < prices.length; i++){dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);dp[i][1] = Math.max(dp[i - 1][1], ((i - 2) >= 0 ? dp[i - 2][0] : 0) - prices[i]);}return Math.max(dp[prices.length - 1][0], dp[prices.length - 1][1]);}
}
77. 戳气球
有 n 个气球,编号为0 到 n - 1,每个气球上都标有一个数字,这些数字存在数组 nums 中。
现在要求你戳破所有的气球。戳破第 i 个气球,你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。 这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界,那么就当它是一个数字为 1 的气球。
求所能获得硬币的最大数量。
示例 1:
输入:nums = [3,1,5,8]
输出:167
解释:
nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins = 315 + 358 + 138 + 181 = 167
解析
固定DP区间,而不固定爆破的气球,dp[i][j] 表示 i 到 j 之间能获得最大金币,不包括i,j边界(戳爆中间,两段不戳爆)
0<= i < k < j <=n + 1 符合这样的位置关系,只管最后一个戳爆的气球!k是最后一个戳爆的气球,分治思想dp[i][k]前半部分,dp[k][j]后半部分
class Solution {public int maxCoins(int[] nums) {int n = nums.length;int[] helper = new int[n + 2];// 固定区间,而不固定爆破的气球// dp[i][j] 表示 i 到 j 之间能获得最大金币,不包括i,j边界,戳爆中间,两段不戳爆int[][] dp = new int[n + 2][n + 2];helper[0] = helper[n + 1] = 1;for(int i = 1; i < n + 1; i++){helper[i] = nums[i - 1];}// 0<= i < k < j <=n + 1 符合这样的位置关系,从后往前戳破气球!for(int i = n - 1; i >= 0; i--){for(int j = i + 2; j < n + 2; j++){for(int k = i + 1; k < j; k++){//k是最后一个戳爆的气球int sum = helper[i] * helper[k] * helper[j];sum += dp[i][k] + dp[k][j];dp[i][j] = Math.max(dp[i][j], sum);}}}return dp[0][n + 1];}
}
78. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
解析
完全背包
代码
class Solution {public int coinChange(int[] coins, int amount) {int[] dp = new int[amount + 1];// dp[i] 金额 i所需的最少硬币Arrays.fill(dp, amount + 1);dp[0] = 0;//0 元 0 种for(int i = 0; i < coins.length; i++){//先遍历硬币,物品for(int j = coins[i]; j < amount + 1; j++){//遍历金额,容量dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1); }}return dp[amount] == amount + 1 ? -1 : dp[amount];}
}
79. 打家劫舍 III
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
输入: root = [3,2,3,null,3,null,1]
输出: 7
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7
解析
使用后序遍历,对于根的计算分为打劫和不打劫两种
class Solution {public int rob(TreeNode root) {if(root == null) return 0;int[] res = dfs(root);//int[0] 表示不打劫,int[1] 表示打劫return Math.max(res[0], res[1]);}private int[] dfs(TreeNode node){if(node == null) return new int[]{0, 0};//后序遍历int[] left = dfs(node.left);int[] right = dfs(node.right);int[] res = new int[2];//不打劫当前节点res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);//打劫当前节点res[1] = node.val + left[0] + right[0];return res;}
}
80. 比特位计数
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1:
输入:n = 2
输出:[0,1,1]
解释:
0 --> 0
1 --> 1
2 --> 10
示例 2:
输入:n = 5
输出:[0,1,1,2,1,2]
解释:
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
解析
对于任何整数都有, x = x &(x - 1),最后一位的1变为0,然后计数
代码
class Solution {public int[] countBits(int n) {//res[i] 第i个有多少个1int[] res = new int[n + 1];for(int i = 0; i < n + 1; i++){int count = 0;int temp = i;while(temp != 0){count++;temp = temp & (temp - 1);//将最后一个位从1变为0}res[i] = count;}return res;}
}
81. 前 K 个高频元素
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
解析
在这里,我们可以利用堆的思想:建立一个大顶堆,然后遍历「出现次数数组」
class Solution {public int[] topKFrequent(int[] nums, int k) {int[] res = new int[k];Map<Integer, Integer> map = new HashMap<>();for(int num : nums){map.put(num, map.getOrDefault(num, 0) + 1);}//大根堆PriorityQueue<Integer> pq = new PriorityQueue<>((x, y) -> map.get(y) - map.get(x));for(Integer key : map.keySet()){pq.offer(key);}for(int i = 0; i < k; i++){res[i] = (int)pq.poll();}return res;}
}
82. 字符串解码
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
示例 1:
输入:s = “3[a]2[bc]”
输出:“aaabcbc”
解析
双栈
class Solution {public String decodeString(String s) {// 栈Stack<Integer> stack = new Stack<>();// 临时结果栈Stack<StringBuilder> temp = new Stack<>();temp.push(new StringBuilder());// 字符串长度、当前的乘数int len = s.length(), mul = 0;for (int i=0; i<len; i++) {char c = s.charAt(i);if (c >= '0' && c <= '9') {// 是数字,则累计mul = mul * 10 + (c - '0');} else if (c == '[') {// 遇到左边框,新增一个临时过程stack.push(mul);temp.push(new StringBuilder());mul = 0;} else if (c == ']') {// 遇到右边框,处理临时过程到上一个临时过程StringBuilder t = temp.pop();temp.peek().append(t.toString().repeat(stack.pop()));} else {// 遇到字符串,拼接到当前的临时过程temp.peek().append(c);}}return temp.pop().toString();}
}
83. 除法求值
给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
另有一些以数组 queries 表示的问题,其中 queries[j] = [Cj, Dj] 表示第 j 个问题,请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。
返回 所有问题的答案 。如果存在某个无法确定的答案,则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串,也需要用 -1.0 替代这个答案。
注意:输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果。
示例 1:
输入:equations = [[“a”,“b”],[“b”,“c”]], values = [2.0,3.0], queries = [[“a”,“c”],[“b”,“a”],[“a”,“e”],[“a”,“a”],[“x”,“x”]]
输出:[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释:
条件:a / b = 2.0, b / c = 3.0
问题:a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
结果:[6.0, 0.5, -1.0, 1.0, -1.0 ]
解析
将其转换为图,并使用带权重的并查集来模拟
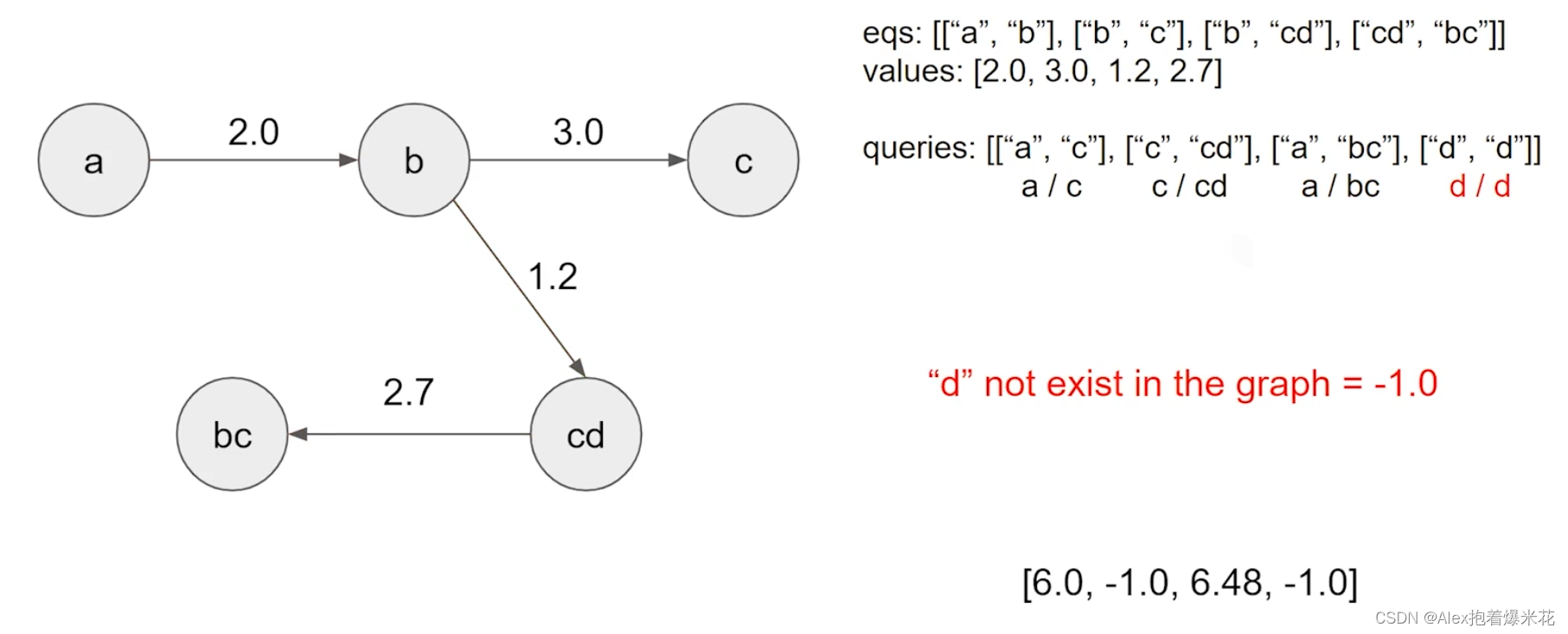
代码
class Solution {public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {UnionFind union = new UnionFind();int i = 0;for(List<String> eq: equations){String a = eq.get(0);String b = eq.get(1);double value = values[i++];union.union(a, b, value);}double[] res = new double[queries.size()];i = 0;for(List<String> query: queries){String x = query.get(0);String y = query.get(1);res[i++] = union.query(x, y);}return res;}//带权重的并查集private class UnionFind{private Map<String, String> parent;private Map<String, Double> weight;public UnionFind(){parent = new HashMap<>();weight = new HashMap<>();}public void union(String x, String y, double value){parent.putIfAbsent(x, x);parent.putIfAbsent(y, y);weight.putIfAbsent(x, 1.0d);weight.putIfAbsent(y, 1.0d);String xRoot = find(x);String yRoot = find(y);if (!xRoot.equals(yRoot)) {parent.put(xRoot, yRoot);weight.put(xRoot, weight.get(y) * value / weight.get(x));}}//找到根节点public String find(String x){if(!parent.get(x).equals(x)){String oldPatient = parent.get(x);parent.put(x, find(parent.get(x)));weight.put(x, weight.get(oldPatient) * weight.get(x));}return parent.get(x);}public double query(String x, String y) {if (!parent.containsKey(x) || !parent.containsKey(y)) {return -1.0d;}String xRoot = find(x);String yRoot = find(y);if (xRoot.equals(yRoot)) {return weight.get(x) / weight.get(y);} else {return -1.0d;}}}}
84. 根据身高重建队列
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释:
编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
解析
(套路):一般这种数对,还涉及排序的,根据第一个元素正向排序,根据第二个元素反向排序,或者根据第一个元素反向排序,根据第二个元素正向排序,往往能够简化解题过程。
本题先第一个元素逆序,然后第二个元素升序,接着插队
class Solution {public int[][] reconstructQueue(int[][] people) {//数组的第一个元素进行逆序,数组第二个元素正序Arrays.sort(people, (x, y) -> {if(x[0] == y[0]){return x[1] - y[1];//升序}else{return y[0] - x[0];//降序}});//再插队,根据下标k进行插队List<int[]> res = new ArrayList<>();for(int[] p : people){res.add(p[1], p);}return res.toArray(new int[res.size()][0]);}
}
85. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
解析
0,1 背包问题
代码
class Solution {public boolean canPartition(int[] nums) {// 0 1背包问题int n = nums.length;int sum = 0; //统计nums的总数for(int num : nums){sum += num;}if(sum % 2 != 0) return false;int target = sum / 2;int[] dp = new int[target + 1];//dp[i] 表示第 i 个正整数的元素和// 0 1 背包模板for(int i = 0; i < n; i++) {for(int j = target; j >= nums[i]; j--) {// 重量和价值都为nums[i]dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);}}return dp[target] == target;}
}86. 路径总和 III
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。

输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出:3
解释:和等于 8 的路径有 3 条,如图所示
解析
先序递归遍历每个节点,再以每个节点作为起始点递归寻找满足条件的路径,双重递归
代码
class Solution {long path = 0;public int pathSum(TreeNode root, int targetSum) {//先序遍历每个结点,然后每个结点作为起始点递归查找if(root == null) return 0;sum(root, targetSum);pathSum(root.left, targetSum);pathSum(root.right, targetSum);return (int)path;}private void sum(TreeNode root, long targetSum){if(root == null) return;targetSum -= root.val;if(targetSum == 0) path++;sum(root.left, targetSum);sum(root.right, targetSum);}
}
