红黑树(Insert())
文章目录
- 红黑树
- 代码
- 红黑树性质
- 红黑树vsAVL树
- 红黑树的实现
- Insert()
- 情况一:如果我插入的新节点时红色的
- 情况二:叔叔是黑色或者不存在
- 情况三: cur红,p为红,g为黑,u不存在或者为黑-双旋
- 检查
- erase()
- 红黑树vsAVL树
- 红黑树的应用:
红黑树
二叉搜索树
代码
红黑树性质
- 每个节点不是黑色就是红色.
- 根节点是黑色
- 红色节点的孩子节点都是黑色的,所以不存在连续的红色.
- 对于节点,从该节点到所有后代叶子节点的简单路径上,包含相同数目的黑色节点。
- 这里的路径不是到叶子结点中止,而是到NULL。
- 节点个数,最长路径不超过最短路径的2倍。最短路径是全黑,最长路径就是一黑一红。假设每条路径黑节点的数量是N,N<=任意路径长度<=2N
- 每个叶子节点都是黑色的,这时候的叶子结点是NULL不是平常的叶子结点。在数路径的时候看的不是叶子结点而是NULL的个数,来保证每条路径黑色节点的数目是相等的.
红黑树vsAVL树
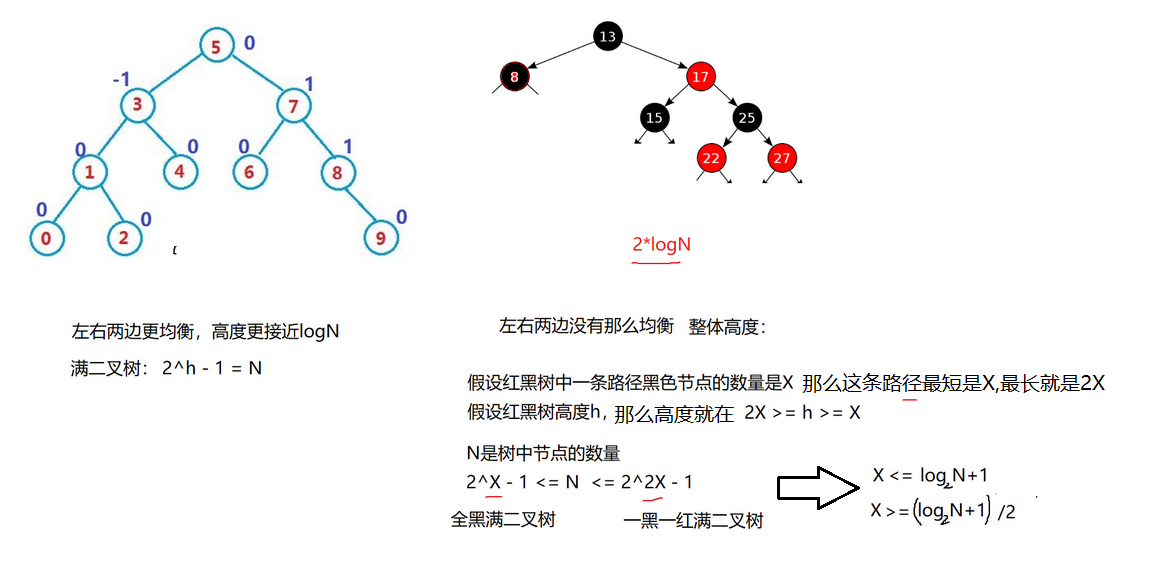
AVL树是严格平衡树的左右相差不超过2,AVL左右两端更加均衡,高度更接近logN。红黑树是近似平衡,红黑树两边最坏情况是2logN。AVL树效率更高.
内存中搜索是差不多的,logN足够小,CPU对于这种很小基数的2倍是很快的,几乎无差别,假设是10亿个数,AVL树放30层,红黑树可能是60层,查找30次和60次对于CPU很小.但是AVL是旋转了很多次,红黑树是不一定旋转的。所以综合来说红黑树更优.
红黑树的实现
Insert()
-
第一次插入是插入那个节点好?
插入黑节点或者红结点就是在违反规则,所以需要考虑那个代价更小,所以选择红结点。
-
如果增加叶子结点是黑节点,那么别的路径的黑节点个数怎么平衡?影响太大。
-
如果插入的是红色,可能父亲是黑色,就没问题;如果父亲是红色就不行,这两种存在概率问题,有空可钻.
-
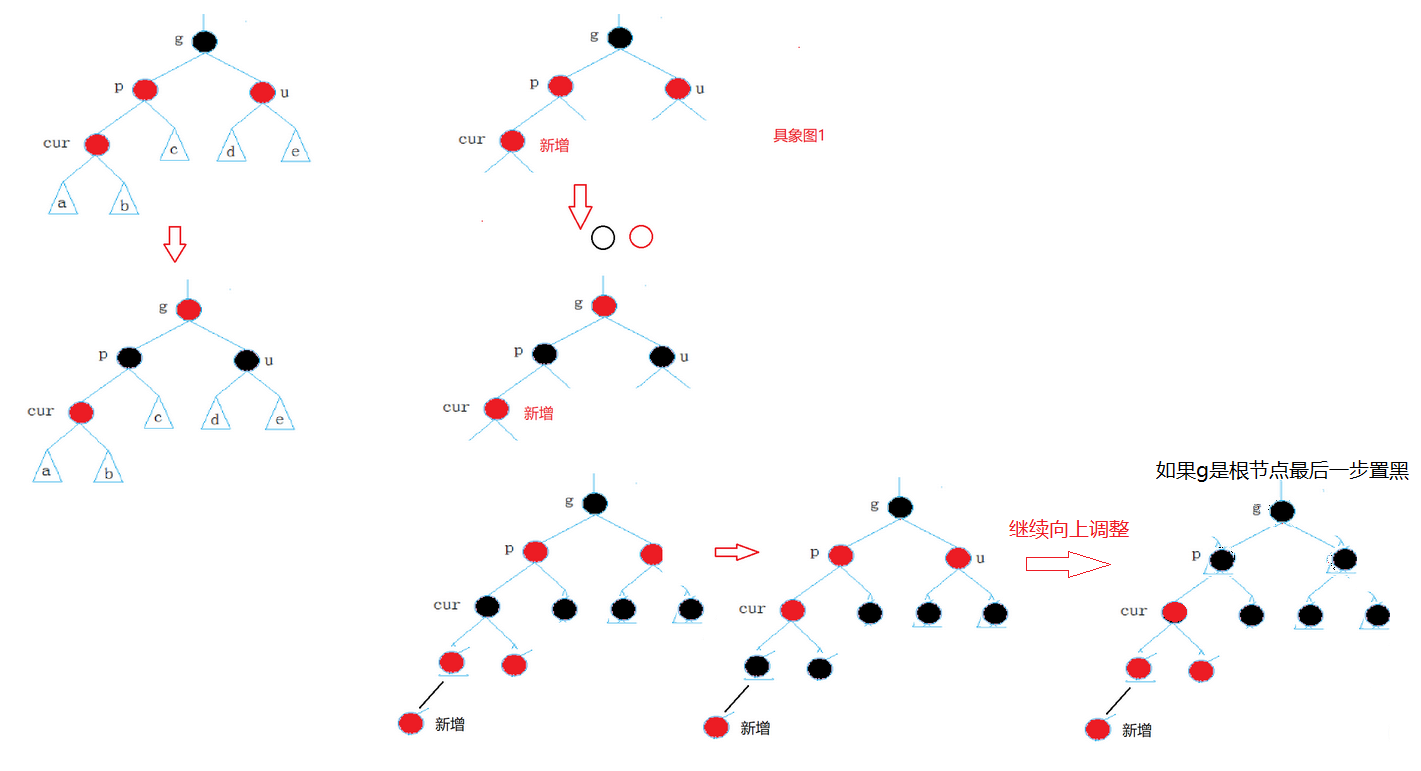
情况一:如果我插入的新节点时红色的
父节点是红的,祖父一定是黑的,(没有连续的红结点),所以看叔叔节点,如果是红结点,那么只需要将parent和uncle节点都改为黑色,祖父g变成红色(因为祖父不一定是根节点,所以我要保证所有路径黑节点个数相同)
如果g->parent是红色的,就需要cur=g,将祖父当成新增,继续向上调整。如果g-parent是黑色就可以结束了。所以就存在cur可能不是新增节点了,是某一个新增节点的祖父.
- 所以cur可能是新增,也有可能是新增的祖父节点的n次。
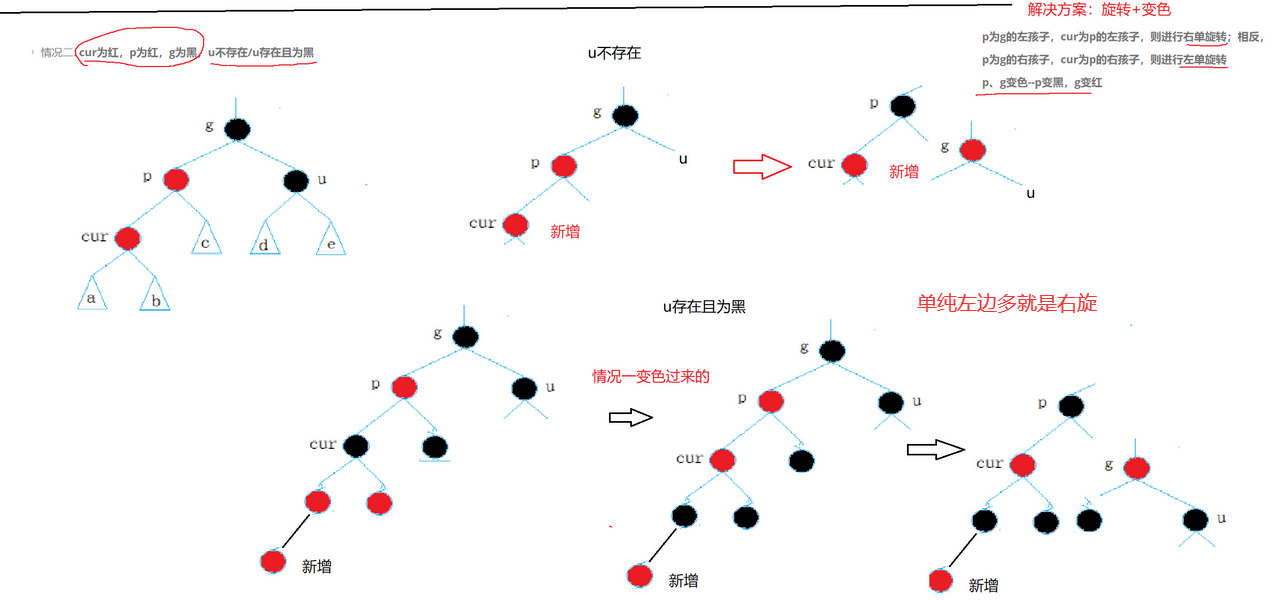
情况二:叔叔是黑色或者不存在
单纯变色不行了,因为最长路径已经超过了最短路径的2倍,就需要旋转一下.旋转的目的就是保持搜索树降低他的高度,让他左右均衡.所以是旋转加变色,先根节点变黑。旋转又分为左右单旋和双旋的情况
- 右单旋图示(左单旋同理)
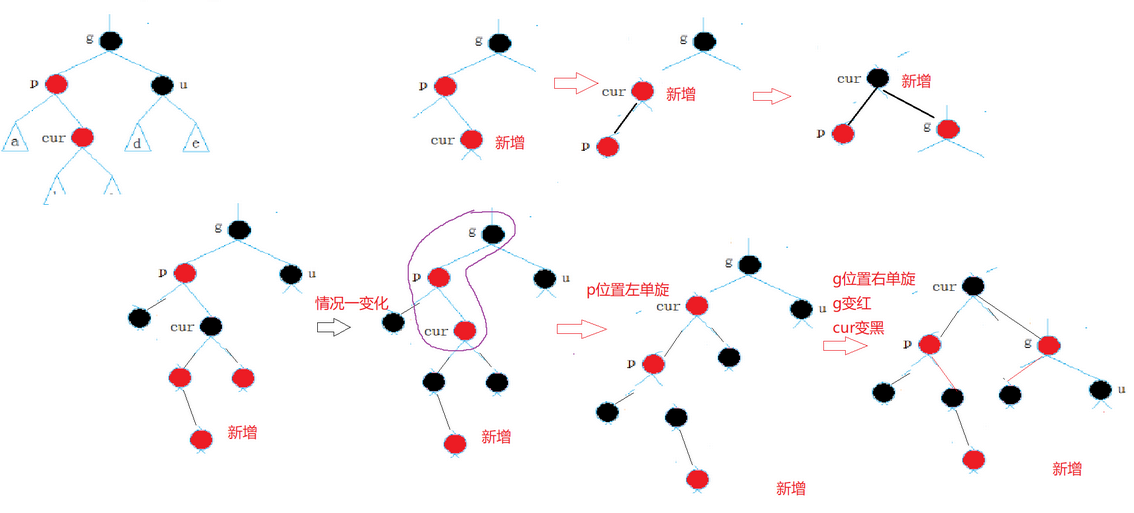
情况三: cur红,p为红,g为黑,u不存在或者为黑-双旋
折线,走单旋是没有效果的,只是把左边高变为右边高.所以走双旋.
p为g的左孩子,cur为p的右孩子,则针对p做左单旋转,然后针对g做右单旋
p为g的右孩子,cur为p的左孩子,则针对p做右单旋转.然后针对g做左单旋
检查
完成之后,编译执行正确只能保证这是一棵搜索树,对于红黑树还需要进一步检验。
- 根节点的颜色必须是黑色
- 如果节点是红色,直接验证他的父亲是不是红色,验证孩子的可能性太多
- 前序遍历就是深度优先遍历,路径中统计黑节点个数就行,给定参考值
banchmark某一条路径的比如最左路径,遍历一条路径,就将这条路径的值blackNum和基准值比较一次,看看每条路径的黑节点个数是否相等.
bool IsBalance(){if (_root && _root->_color == RED){cout << "根节点不是黑色" << endl;return false;}int banchmark = 0;Node* left = _root;while (left){if (left->_color == BLACK){++banchmark;}left = left->_left;}int blackNum = 0;return _IsBalance(_root, banchmark, blackNum);}
bool _IsBalance(Node* root, int banchmark, int blackNum){if (root == nullptr){if (banchmark != blackNum){cout << "存在路径黑色节点的数量不相等" << endl;return false;}return true;}if (root->_color == RED && root->_parent->_color == RED){cout << "连续出现红色节点" << endl;return false;}if (root->_color == BLACK){++blackNum;}return _IsBalance(root->_left, banchmark, blackNum)&& _IsBalance(root->_right, banchmark, blackNum)}
erase()
大佬博客
红黑树vsAVL树
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O(logN),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多.
红黑树的应用:
- C++ STL库 – map/set、mutil_map/mutil_set
- Java 库
- linux内核
- 其他一些库
