前缀和算法 -- 寻找数组的中心坐标

个人主页:Lei宝啊
愿所有美好如期而遇

本题链接
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
输入描述
给定一个数组,接口为int pivotIndex(vector<int>& nums)
输出描述
我们以示例1为例画图解释:

我们返回下标3。
算法分析
算法一:暴力求解
直接遍历数组,外层遍历到哪个i,里层就遍历一次整个数组求和比较,时间复杂度为O(N^2),这种时间复杂度我们不能接受。
算法二:前缀和
方法一:
我们创建dp表,dp[i]表示从下标0到下标i的元素和,用一个变量sum记录。
预处理dp表

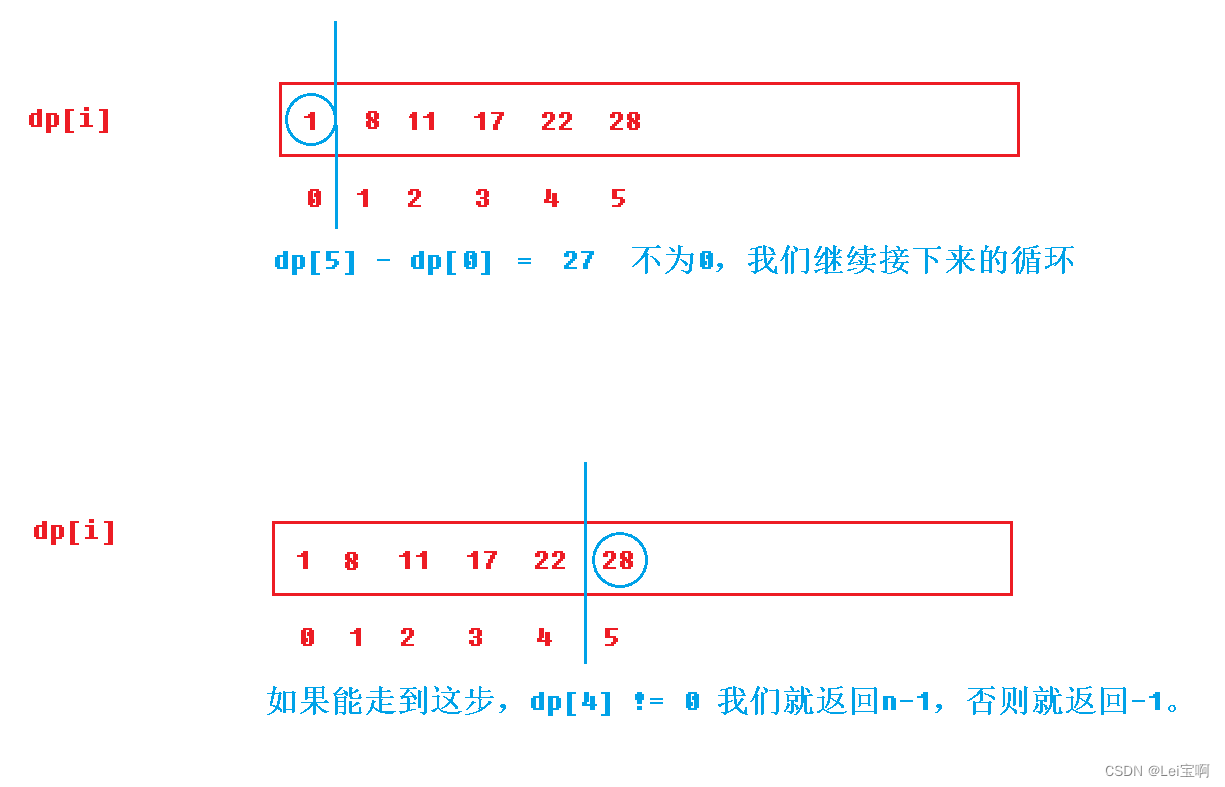
使用dp表计算
接下来我们仍然是遍历数组,但是我们需要提前计算出边界问题,一个是0位置的边界,一个是n-1位置的边界(这个边界在循环后判断),我们根据上图来判断一下0这个边界,0的左边什么都没有,题目使其和为0,所以我们判断dp[n-1] - dp[0] == 0就return 0,否则继续我们的循环,我们的循环从1开始,到n-1边界结束,然后判断这个边界,即dp[n-2] == 0,我们return n-1; 否则就是没有找到这样的中间下标,我们返回-1。
解题源码:
class Solution
{
public:int pivotIndex(vector<int>& nums){int n = nums.size();int sum = 0;vector<int> dp(n, 0);//dp[i]表示i位置及其前部分的和for (int i = 0; i < n; i++){sum += nums[i];dp[i] = sum;}if (dp[n - 1] - dp[0] == 0) return 0;for (int i = 1; i < n - 1; i++){if (dp[i - 1] == dp[n - 1] - dp[i]){return i;}}if (dp[n - 2] == 0) return n - 1;return -1;}
};方法二:
我们创建前缀和dp表和后缀和dp表,这里的dp[i]和我们方法一的含义是不同的,这里的dp[i]意为下标0到下标i-1的和,那么dp[i-1]意为下标0到下标i-2的和,以此类推。
预处理dp表
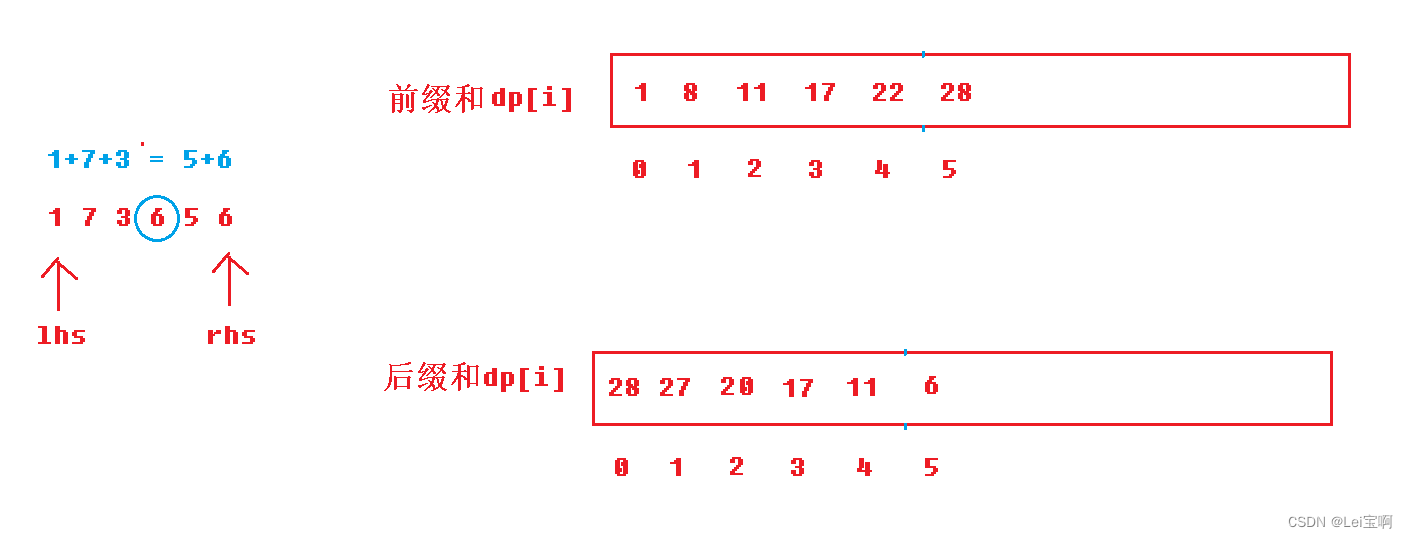
前缀和是从前往后加,后缀和是从后往前加,什么意思呢?我们看图
那么写成代码如何推导这两个dp表呢?
dp[i]是下标0到下标i-1的和,dp[i-1]是下标0到下标i-2元素的和......,dp[1]就是dp[0]加上下标为0元素的值,dp[0]我们初始化为0。因为题目规定下标为0或者右边的边界时,左边元素和,右边元素和为0,所以我们dp[0],dp[n-1]初始化为0。
我们写成公式就是
- 前缀 dp[i] = dp[i-1] + nums[i-1],i从1开始
- 后缀 dp[i] = dp[i+1] + nums[i+1],i从n-2开始
使用dp表计算
我们使前缀dp[i] 与 后缀dp[i]做比较,相等则返回下标,循环外则返回-1。
解题源码
class Solution
{
public:int pivotIndex(vector<int>& nums){int n = nums.size();vector<int> f(n, 0);vector<int> g(n, 0);for (int i = 1; i < n; i++)f[i] = f[i - 1] + nums[i - 1];for (int i = n - 2; i >= 0; i--)g[i] = g[i + 1] + nums[i + 1];for (int i = 0; i < n; i++){if (f[i] == g[i])return i;}return -1;}
};其实博主个人感觉方法一好理解一点,不过方法二的思想值得我们去学习,同时不要死记前缀和,后缀和公式,dp[i]的情况是不同的,就像我们的方法一和方法二,他们中的dp[i]含义就不同,我们需要理解的是思想。
