代码随想录27期|Python|Day24|回溯法|理论基础|77.组合
图片来自代码随想录
回溯法题目目录
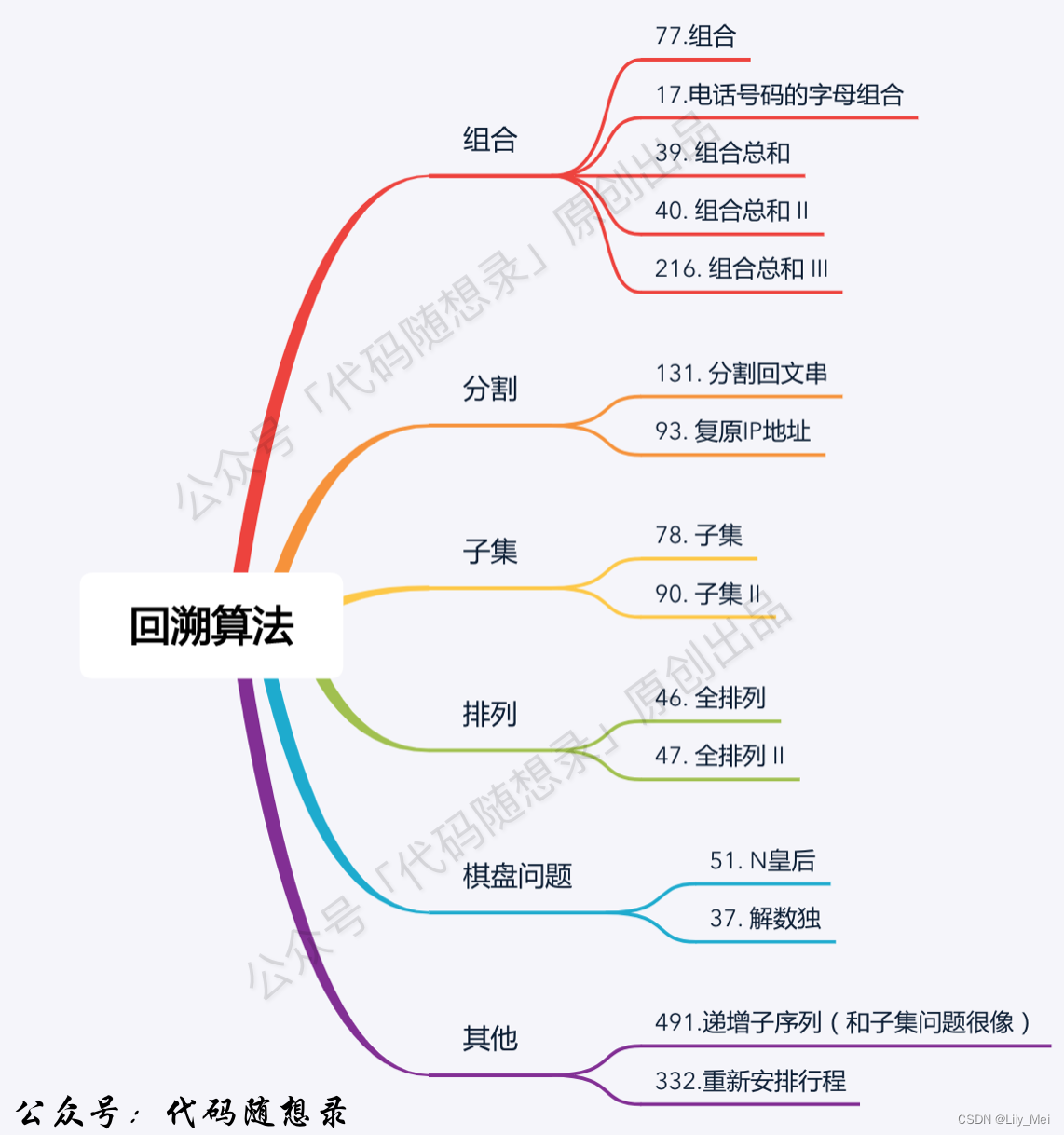
理论基础
定义
回溯法也可以叫做回溯搜索法,它是一种搜索的方式。
回溯是递归的副产品,只要有递归就会有回溯。回溯函数也就是递归函数,指的都是一个函数。
基本问题
- 组合问题(无序):N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题(有序):N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
解题模版
所有回溯问题都可以抽象为一个树问题。
返回值和参数
一般返回值都是void。参数需要根据实际情况确定。
void backtracking(参数)终止条件
类似树的结构,一般是找到叶子节点之后返回,必要的时候需要保存结果。
if (终止条件) {存放结果;return;
}遍历过程
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果
}
需要注意集合大小和分支数量是对应的。以及在回溯过程当中在每一次回溯之后需要撤销这一步的处理内容。
77. 组合

class Solution(object):def combine(self, n, k):""":type n: int:type k: int:rtype: List[List[int]]"""res = []self.backtracking(n, k, 1, [], res)return resdef backtracking(self, n, k, start_idx, path, res):# 终止条件if len(path) == k:res.append(path[:]) # 加入resreturn # 回溯for i in range(start_idx, n + 1):path.append(i)self.backtracking(n, k, i + 1, path, res) # 起始位置变成i+1path.pop() # 回溯第24天完结🎉
