哈夫曼解码
【问题描述】
给定一组字符的Huffman编码表(从标准输入读取),给定一个用该编码表进行编码的Huffman编码文件(存在当前目录下的in.txt中),编写程序对Huffman编码文件进行解码。
例如给定的一组字符的Huffman编码表为:
6
1:111
2:0
+:110
*:1010
=:1011
8:100
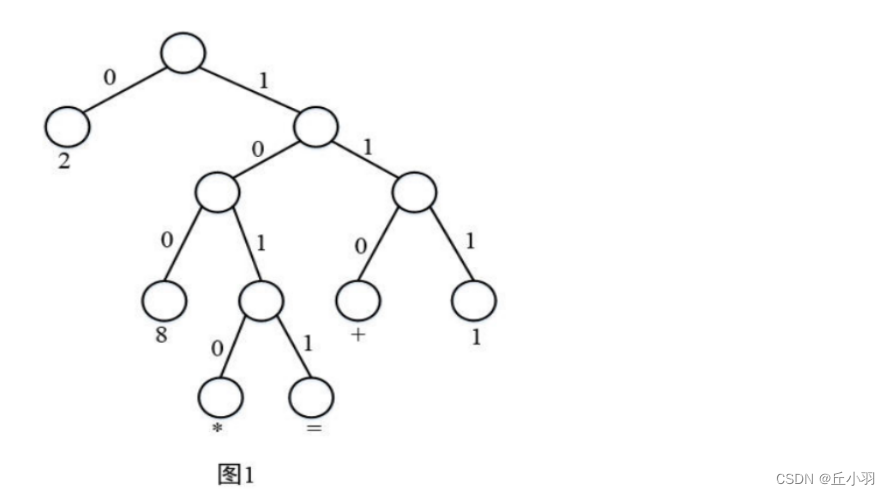
第一行的6表示要对6个不同的字符进行编码,后面每行中冒号(:)左边的字符为待编码的字符,右边为其Huffman编码,冒号两边无空格。对于该编码表,对应的Huffman树(树中左分支表示0,右分支表示1)应为:
假如Huffman编码文件in.txt中的内容(由0和1字符组成的序列)为:
111011010010110101010011001100
则遍历上述Huffman树即可对该文件进行解码,解码后的文件内容为:
12+8=2*8+2+2
【输入形式】
先从标准输入读入待编码的字符个数(大于等于2,小于等于30),然后分行输入各字符的Huffman编码(先输入字符,再输入其编码,字符和编码中间以一个英文字符冒号:分隔),编码只由0和1组成。
Huffman编码文件为当前目录下的in.txt文本文件,即:其中的0和1都是以单个字符的形式存储,文件末尾有一个回车换行符。
【输出形式】
将解码后的文件内容输出到标准输出上
【样例输入】
6
1:111
2:0
+:110
*:1010
=:1011
8:100
假如in.txt中的内容为:
1110110100101101010100110011001100
【样例输出】
12+8=2*8+2+2
【样例说明】
从标准输入读取了6个字符的Huffman编码,因为规定Huffman树中左分支表示0,右分支表示1,所以利用该编码表可构造上述Huffman树(见图1)。遍历该Huffman树对编码文件in.txt的进行解码,即可得到解码后的原文件内容。
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include<string>
#include <stdio.h>
using namespace std;
class node
{
public:
int data;//操作数
char op;//操作符
bool flag;//true表示操作数,false表示操作符
node*lchild;
node*rchild;
node():data(0),op(0),flag(true),lchild(nullptr),rchild(nullptr){};
node(int n):data(n),op(0),flag(false),lchild(nullptr),rchild(nullptr){};
node(int n,char c):data(n),op(c),flag(true),lchild(nullptr),rchild(nullptr){}
};
class myTree
{public:node*root;void creatMytree(int n);
};
void removeSpace(string &str)
{std::string::size_type index = 0;if(!str.empty()){while((index=str.find(' ',index))!=string::npos){str.erase(index,1);}}
}
void myTree::creatMytree(int n)
{root = new node();//创建根节点for(int i=0;i<n;i++){string input;cin>>input;removeSpace(input);int colonPos=input.find(':');string path = input.substr(colonPos+1);node*current = root;for(char ch:path){if(ch == '0'){if(!current->lchild){current->lchild = new node();}current = current->lchild;}else if(ch== '1'){if(!current->rchild){current->rchild = new node();}current = current->rchild;}}if(input[0]>='0'&&input[0]<='9'){//获取字符串中的数字int num=stoi(input.substr(0,colonPos));//从输入的字符串中提取第一个冒号之前的数字,并将其转化为整数类型,这在解析二叉树的时候非常实用。便于将字符串转化为数据。//特别是在大于一位数的转化上非常实用。current->data = num;current->flag = true;}else{char num = input[0];current->op = num;current->flag=false;}}
}
void decodeMyTree(node*root,string str)
{node*current = root;int num;while(!str.empty()){num=0;current=root;for(char ch:str){if(ch=='0'){if(current->lchild!=nullptr)current=current->lchild;else break;}else if(ch=='1'){if(current->rchild!=nullptr)current = current->rchild;else break;}num++;}if(current->flag==true){cout<<current->data;}else{cout<<current->op;}str.erase(0,num);}
}
int main(void)
{int n;cin>>n;myTree*t = new myTree();t->creatMytree(n);freopen("in.txt","r",stdin);string str;cin>>str;removeSpace(str);decodeMyTree(t->root,str);return 0;
}【问题描述】
给定一个无向图和一个图顶点,采用邻接表存储无向图,编程输出该图深度优先遍历的顶点序列;删除给定顶点后输出广度优先遍历的顶点序列。
给定的无向图和图顶点满足以下要求:
1、无向图的顶点个数n大于等于3,小于等于100,输入时顶点编号用整数0~n-1表示;
2、无向图在删除给定顶点前后都是连通的;
3、无论何种遍历,都是从编号为0的顶点开始遍历,访问相邻顶点时按照编号从小到大的顺序访问;
4、删除的顶点编号不为0。
【输入形式】
先从标准输入中输入图的顶点个数和边的个数,两整数之间以一个空格分隔,然后从下一行开始分行输入每条边的信息(用边两端的顶点编号表示一条边,以一个空格分隔顶点编号,边的输入次序和每条边两端顶点编号的输入次序可以是任意的,但边不会重复输入),最后在新的一行上输入要删除的顶点编号。
【输出形式】
分行输出各遍历顶点序列,顶点编号之间以一个空格分隔。先输出删除给定顶点前的深度优先遍历顶点序列,再输出删除给定顶点后的广度优先遍历顶点序列。
【样例输入】
9 10
0 1
0 2
1 3
1 4
1 8
2 5
2 7
3 6
5 7
6 8
3
【样例输出】
0 1 3 6 8 4 2 5 7
0 1 2 4 8 5 7 6
【样例说明】
输入的无向图有9个顶点,10条边(如下图所示),要删除的顶点编号为3。

#include<iostream>
#include <vector>
#include<queue>
#include<list>
#include <string>
#include<algorithm>
using namespace std;
class Graph
{int V;//顶点个数list<int>*adj;//邻接表 public:Graph(int V);//构造函数void addEdge(int v,int w);//添加边void DFS(int v,vector<bool>&visited);//深度优先搜索void BFS(int s);//广度优先搜索void removeVertex(int v);//删除节点void printDFS(int start);//输出深度优先搜索序列void printBFS(int start);//输出广度优先搜索序列
};
Graph::Graph(int V)//构造函数,将实参V传递给形参V,表示有V个顶点
{this->V = V;adj = new list<int>[V];//邻接表有v个元素
}
void Graph::addEdge(int v,int w)
{adj[v].push_back(w);//添加w的边添加到v的邻接表中adj[w].push_back(v);//添加v的边到w的邻接表中
}
void Graph::DFS(int v,vector<bool>&visited)//邻接表的深度优先搜索实现
{visited[v]=true;//索引为v的元素设置为true,表示当前节点v已经被访问过。cout<<v<<" ";adj[v].sort();//邻接表排序list<int>::iterator i;for(i = adj[v].begin();i!=adj[v].end();i++)if(!visited[*i])DFS(*i,visited);
}
void Graph::BFS(int s)//邻接表的广度优先搜索实现
{vector<bool>visited(V,false);queue<int>queue;visited[s]=true;queue.push(s);while(!queue.empty()){s=queue.front();cout<<s<<" ";queue.pop();adj[s].sort();for(auto i=adj[s].begin();i!=adj[s].end();i++)if(!visited[*i]){visited[*i]=true;queue.push(*i);}}
}
void Graph::removeVertex(int v)
{for(int i=0;i<V;i++){adj[i].remove(v);}adj[v].clear();
}
void Graph::printDFS(int start)
{vector<bool>visited(V,false);DFS(start,visited);cout<<endl;
}
void Graph::printBFS(int start)
{BFS(start);cout<<endl;
}
int main()
{int n,m;cin>>n>>m;Graph g(n);int a,b;for(int i=0;i<m;i++){cin>>a>>b;g.addEdge(a,b);}int toDelete;cin>>toDelete;g.printDFS(0);g.removeVertex(toDelete);g.printBFS(0);return 0;
}
