当前位置：首页 > news >正文

大话数据结构-栈

news 2025/8/20 21:16:33

1 概述

栈（Stack）是限定仅在表尾进行插入和删除操作的线性表。

允许插入和删除的一端称为栈顶（top），另一端称为栈底（bottom），不含任何数据元素的栈称为空栈，栈又称为后进先出（Last In First Out）的线性表，简称LIFO结构。

栈的插入操作，叫作进栈，也称压栈、入栈；栈的删除操作，叫作出栈，也有的叫作弹栈。

2 栈的抽象数据类型

ADT 栈(Stack)Data：同线性表。元素具有相同的类型，相邻元素具有前驱和后继关系。Operation：init(int maxSize)：初始化操作，建立一个空栈；destroy()：若栈存在，则销毁它；clear()：清空栈；isEmpty()：若栈为空，返回true，否则返回false；getTop()：若栈存在且非空，则返回栈顶元素；push(DataType e)：进栈；pop()：出栈；length()：返回栈的元素个数；
endADT

3 顺序存储结构

3.1 概述

基于栈的特殊性，我们可以考虑使用数组来实现栈，令数组的下标为0的元素作为栈底元素，并定义一个top指针来指向栈顶元素在数组中的位置：

3.2 进栈操作

把数据添加到top指向的下标的下一个下标，然后把top下移一位即可：

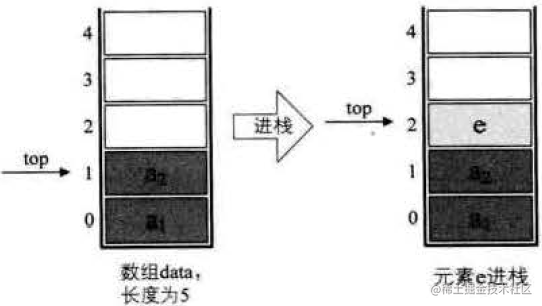
代码实现如下：

/*** 进栈操作** @param value 待进栈的值* @throws RuntimeException 栈满时抛出* @author Korbin* @date 2023-01-10 11:32:41**/
public void push(T value) {if (top == maxSize - 1) {throw new RuntimeException("fulled");}data[++top] = value;
}

3.3 出栈操作

返回top所在的当前元素，并令top减1即可：

 /*** 出栈** @return 出栈的元素* @throws RuntimeException 栈空时抛出异常* @author Korbin* @date 2023-01-10 11:34:49**/
public T pop() {if (top == -1) {throw new RuntimeException("empty stack");}return data[top--];
}

3.4 完整代码

import java.util.Arrays;/*** 栈* <p>* 线性栈顶的数据为一个数组，数组的第一个元素（索引为0）为栈底* <p>* 栈是先进后出的数据结构** @author Korbin* @date 2023-01-10 11:21:07**/
public class Stack<T> {/*** 栈内数据**/private T[] data;/*** 栈的最大长度**/private int maxSize;/*** 栈顶指针，为数组索引* <p>* 值为-1时表示空栈**/private int top = -1;/*** 清空栈**/public void clear() {init(maxSize);}/*** 获取栈顶指针** @return 栈顶指针* @author Korbin* @date 2023-01-10 11:45:08**/public T getTop() {if (top == -1) {throw new RuntimeException("empty stack");}return data[top];}/*** 初始化** @param maxSize 栈的长度* @author Korbin* @date 2023-01-10 11:38:41**/@SuppressWarnings("unchecked")public void init(int maxSize) {this.maxSize = maxSize;data = (T[]) new Object[maxSize];top = -1;}/*** 栈是否为空栈，空栈返回true，否则返回false* <p>* top为-1时为空栈**/public boolean isEmpty() {return top == -1;}/*** 栈的元素个数**/public int length() {return top + 1;}/*** 出栈** @return 出栈的元素* @throws RuntimeException 栈空时抛出异常* @author Korbin* @date 2023-01-10 11:34:49**/public T pop() {if (top == -1) {throw new RuntimeException("empty stack");}return data[top--];}/*** 进栈操作** @param value 待进栈的值* @throws RuntimeException 栈满时抛出* @author Korbin* @date 2023-01-10 11:32:41**/public void push(T value) {if (top == maxSize - 1) {throw new RuntimeException("fulled");}data[++top] = value;}@Overridepublic String toString() {return "Stack{" + "data=" + Arrays.toString(data) + ", stackSize=" + maxSize + ", top=" + top + '}';}}

4 两栈共享空间

4.1 概述

顺序存储的栈使用数组存储数据，将下标为0的元素作为栈底元素，并定义了top指向栈顶元素，定义maxSize确认栈中最大可以存储的元素个数。

这种实现方式可能造成maxSize定义较大，但实际使用的空间较小的情况，因此为了尽可能节省或者说尽可能利用上存储空间，如果有两个栈是相同的数据类型时，可以将两个栈一起放置在一个数组中，栈A以下标为0的元素为栈底，栈B以下标为maxSize-1的元素为栈底，双向进行操作，以最大利用定义好的数组空间。

实现方式并不复杂，只是由原来的只管理一个top，变成管理两个top，只要top1和top2不“见面”，那么数组就可以一直被使用，因此，当top1 + 1 = top2时，才表示栈满了，这时，两个top“见面”了。

4.2 代码实现

import java.util.Arrays;/*** 双向顺序栈* <p>* 一个数组中包含两个栈，栈1的栈顶索引为0,栈2的栈顶索引为n-1* <p>* 当栈1的栈顶索引为-1时，表示栈1为空栈* <p>* 当栈2的栈顶索引为n时，表示栈2为空栈** @author Korbin* @date 2023-01-10 11:54:20**/
public class BidirectionalStack<T> {/*** 栈内数据**/private T[] data;/*** 栈的最大长度**/private int maxSize;/*** 栈1的栈顶指针，为数组索引* <p>* 值为-1时表示空栈**/private int top1 = -1;/*** 栈2的栈顶指针，为数组索引* <p>* 值为stackSize时表示空栈**/private int top2 = -1;/*** 清空栈** @param stackNumber 栈的数量，只能为1或2* @throws RuntimeException 当栈为空或stackNumber不为1和2时抛出异常* @author Korbin* @date 2023-01-16 10:14:32**/public void clear(int stackNumber) {if (stackNumber == 1) {for (int i = 0; i <= top1; i++) {data[i] = null;}top1 = -1;} else if (stackNumber == 2) {for (int i = maxSize - 1; i >= top2; i--) {data[i] = null;}top2 = maxSize;} else {throw new RuntimeException("error stack number");}}/*** 获取栈1的栈顶指针** @param stackNumber 栈的数量，只能为1或2* @return 栈顶指针* @throws RuntimeException 当栈为空或stackNumber不为1和2时抛出异常* @author Korbin* @date 2023-01-10 11:45:08**/public T getTop(int stackNumber) {if (stackNumber == 1) {if (top1 == -1) {throw new RuntimeException("empty stack");}return data[top1];} else if (stackNumber == 2) {if (top2 == maxSize) {throw new RuntimeException("empty stack");}return data[top2];} else {throw new RuntimeException("error stack number");}}/*** 初始化** @param maxSize 栈的长度* @author Korbin* @date 2023-01-10 11:38:41**/@SuppressWarnings("unchecked")public void init(int maxSize) {this.maxSize = maxSize;this.top1 = -1;this.top2 = maxSize;data = (T[]) new Object[maxSize];}/*** 栈是否为空** @param stackNumber 栈的数量，只能为1或2* @return 为空返回true，不为空返回false* @throws RuntimeException 当栈为空或stackNumber不为1和2时抛出异常* @author Korbin* @date 2023-01-16 10:16:29**/public boolean isEmpty(int stackNumber) {if (stackNumber == 1) {return top1 == -1;} else if (stackNumber == 2) {return top2 == maxSize;} else {throw new RuntimeException("error stack number");}}/*** 返回栈的元素个数** @param stackNumber 栈的数量，只能为1或2* @return 栈的元素个数* @throws RuntimeException 当栈为空或stackNumber不为1和2时抛出异常* @author Korbin* @date 2023-01-16 10:18:19**/public int length(int stackNumber) {if (stackNumber == 1) {return top1 + 1;} else if (stackNumber == 2) {return maxSize - top2;} else {throw new RuntimeException("error stack number");}}/*** 出栈** @param stackNumber 栈的数量，只能为1或2* @return 出栈的值* @throws RuntimeException 当栈为空或stackNumber不为1和2时抛出异常* @author Korbin* @date 2023-01-10 12:06:56**/public T pop(int stackNumber) {if (stackNumber == 1) {// 栈1出栈if (top1 == -1) {throw new RuntimeException("empty stack");}T result = data[top1];data[top1] = null;top1--;return result;} else if (stackNumber == 2) {// 栈2出栈if (top2 == maxSize) {throw new RuntimeException("empty stack");}T result = data[top2];data[top2] = null;top2++;return result;} else {throw new RuntimeException("error stack number");}}/*** 进栈** @param value       待进栈的值* @param stackNumber 栈的数量，为1或2* @throws RuntimeException 栈满或者stackNumber不为1和2时抛出异常* @author Korbin* @date 2023-01-10 12:03:48**/public void push(T value, int stackNumber) {if (top1 + 1 == top2) {throw new RuntimeException("fulled");}if (stackNumber == 1) {// 栈1进栈data[++top1] = value;} else if (stackNumber == 2) {// 栈2进栈data[--top2] = value;} else {throw new RuntimeException("error stack number");}}@Overridepublic String toString() {return "BidirectionalStack{" + "data=" + Arrays.toString(data) + ", stackSize=" + maxSize + ", top1=" + top1 +", top2=" + top2 + '}';}}

5 栈的链式存储结构

5.1 概述

栈的链式存储结构，简称为链栈，处理方式是，把栈顶放在单链表的头部，用来代替头结点：

栈的结点定义中，用data表示存储的元素，用next表示后继节点：

import lombok.Data;/*** 链栈节点** @author Korbin* @date 2023-01-10 17:12:00**/
@Data
public class StackNode<T> {/*** 节点值**/private T data;/*** 后继节点**/private StackNode<T> next;}

5.2 进栈操作

链栈中定义了两个属性，一为top，指向栈顶元素，一为count，表示的是实际元素的数量。

因此链栈在进栈时，只需要两步操作：

(1) 定义一个新的结点，令其的后继结点指向top结点；

(2) 令top指向新定义的结点；

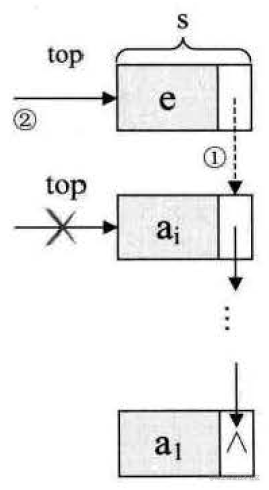
/*** 进栈** @param value 待进栈的节点值* @author Korbin* @date 2023-01-10 17:31:45**/
public void push(T value) {StackNode<T> newNode = new StackNode<>();newNode.setData(value);newNode.setNext(top);top = newNode;count++;
}

5.3 出栈操作

令top指向其后继结点即可：

/*** 出栈** @return 出栈的节点* @throws RuntimeException 栈为空时抛出异常* @author Korbin* @date 2023-01-10 17:38:10**/
public StackNode<T> pop() {if (count == 0) {throw new RuntimeException("empty stack");}StackNode<T> result = top;top = top.getNext();count--;return result;
}

5.4 完整代码

/*** 链栈，即链式存储的栈** @author Korbin* @date 2023-01-10 17:21:26**/
public class LinkStack<T> {/*** 节点数量**/private int count = 0;/*** 栈顶指针**/private StackNode<T> top = null;/*** 清空链栈** @author Korbin* @date 2023-01-16 10:34:55**/public void clear() {init();}/*** 获取栈顶节点** @return 栈顶节点* @author Korbin* @date 2023-01-10 17:34:41**/public StackNode<T> getTop() {return top;}/*** 初始化链栈** @author Korbin* @date 2023-01-16 10:34:55**/public void init() {top = null;count = 0;}/*** 是否为空栈，是则返回true，否则返回false** @return 空栈返回true，否则返回false* @author Korbin* @date 2023-01-16 10:35:29**/public boolean isEmpty() {return count == 0;}/*** 获取总节点数** @return 总节点数* @author Korbin* @date 2023-01-10 17:32:14**/public int length() {return count;}/*** 出栈** @return 出栈的节点* @throws RuntimeException 栈为空时抛出异常* @author Korbin* @date 2023-01-10 17:38:10**/public StackNode<T> pop() {if (count == 0) {throw new RuntimeException("empty stack");}StackNode<T> result = top;top = top.getNext();count--;return result;}/*** 进栈** @param value 待进栈的节点值* @author Korbin* @date 2023-01-10 17:31:45**/public void push(T value) {StackNode<T> newNode = new StackNode<>();newNode.setData(value);newNode.setNext(top);top = newNode;count++;}@Overridepublic String toString() {StringBuilder builder = new StringBuilder("[");if (null != top) {StackNode<T> tmp = top;builder.append(tmp.getData()).append(",");while (null != tmp.getNext()) {builder.append(tmp.getNext().getData()).append(",");tmp = tmp.getNext();}}builder.append("]");return builder.toString();}}

BTW：用Java来描述数据结构可能不是一个好的方式——所有内存的处理都忽略了——也可能是我还学不到家。

6 栈的应用-四则运算表达式求值

6.1 中缀表示法、前缀表示法、后缀表示法

通常我们看到的四则运算，称为中缀表示法比如：

a + b * c - (d + e)

前缀表示法又称波兰表示法，即把运算符放在前面，操作数写在后面，前缀表示法是一种没有括号的表示法，将中缀表示法转化成前缀表示法的步骤为：

(1) 首先按照运算符的优先级对所有的运算单位加括号；

(2) 转前缀则将符号移动到对应括号之前；

(3) 去掉括号；

如上述表达式，我们先将所有运算单位加上括号，我们知道，上述表达式的运算过程应为：

(1) 计算d + e；

(2) 计算b * c；

(3) 计算a + (b * c)；

(4) 计算(a + (b * c)) - (d + e)；

因此，把所有运算单元都加上括号后，表达式变为：

((a + (b * c)) - ( d + e ))

注意，每一步都要加上括号。

然后，我们把每个运算符，都移到到其对应的括号前面，表达式变成：

-(+(a  *(b  c))  +( d  e ))

再把括号省略掉，得到前缀表达式：

- + a * b c + d e

后缀表达式转换方式类似，先加括号：

((a + (b * c)) - ( d + e ))

然后把运算符移到对应括号后面：

((a  (b  c)*)+  ( d  e )+)-

然后去掉括号，得到结果：

a b c * + d e + -

6.2 中缀表达式转前缀表达式的代码实现

代码实现时与手动算法不同，遵循如下过程：

(1) 初始化两个栈：运算符栈S1和储存中间结果的栈S2；

(2) 从右至左扫描中缀表达式；

(3) 遇到操作数时，将其压入S2；

(4) 遇到运算符时，比较其与S1栈顶运算符的优先级：

1) 如果S1为空，或栈顶运算符为右括号“)”，则直接将此运算符入栈；

2) 否则，若优先级比栈顶运算符的较高或相等，也将运算符压入S1；

3) 否则，将S1栈顶的运算符弹出并压入到S2中，然后从S1中取出栈顶元素，再将待处理的元素与栈顶运行符比较，处理方式与第(4)点相同；

(5) 遇到括号时：

1) 如果是右括号“)”，则直接压入S1；

2) 如果是左括号“(”，则依次弹出S1栈顶的运算符，并压入S2，直到遇到右括号为止，此时将这一对括号丢弃；

(6) 重复步骤(2)至(5)，直到表达式的最左边；

(7) 将S1中剩余的运算符依次弹出并压入S2；

(8) 依次弹出S2中的元素并输出，结果即为中缀表达式对应的前缀表达式。

以以下表达式为例：

a + b * c - (d + e)

首先是两个空栈S1和S2：

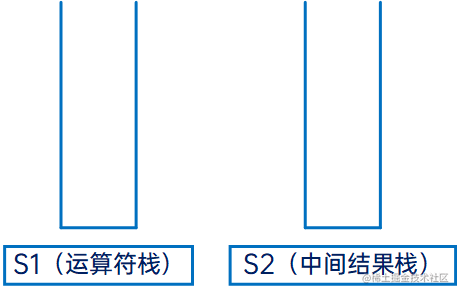
然后是倒序迭代给定的字符串，首先是“)”，右括号直接压入S1：

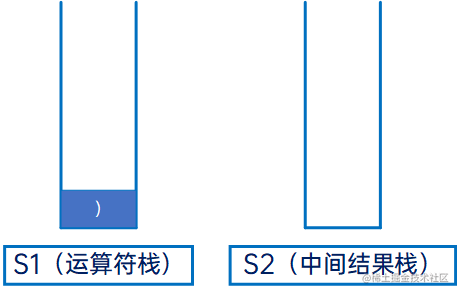
然后是“e”，操作数，直接压入S2：

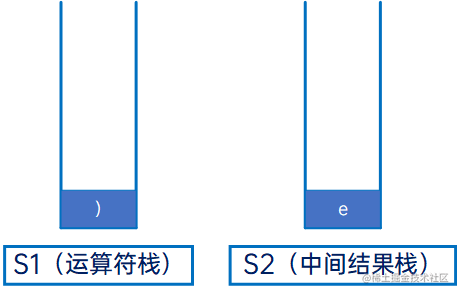
然后是“+”，运算符，与S1的栈顶元素“)”比较，直接入S1栈：

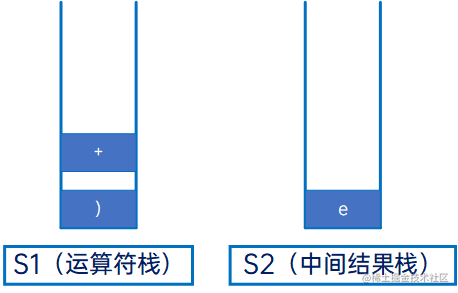
然后是“d”，操作数，直接压入S2：

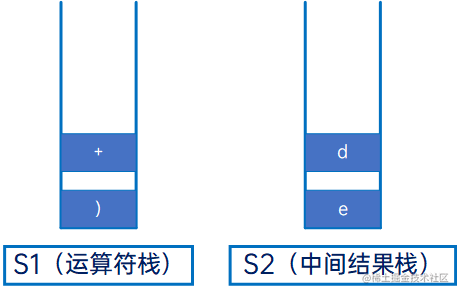
然后是“(”，依次弹出S1的栈顶元素，直到遇到“)”，并抛弃这一对括号：

然后是“-”，与S1的栈顶元素比较，因S1的栈顶元素是空，因此直接进入S1栈：

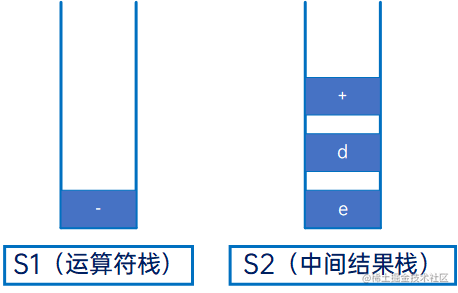
然后是“c”，操作数，直接压入S2：

然后是“*”，与S的栈顶元素“-”比较，优先级较高，因此压入S1：

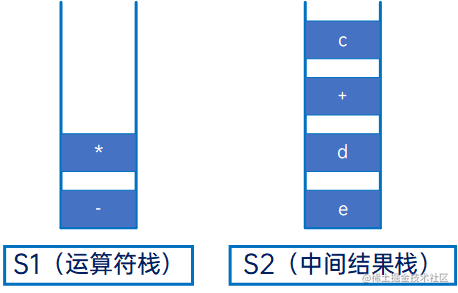
然后是“b”，操作数，直接压入S2：

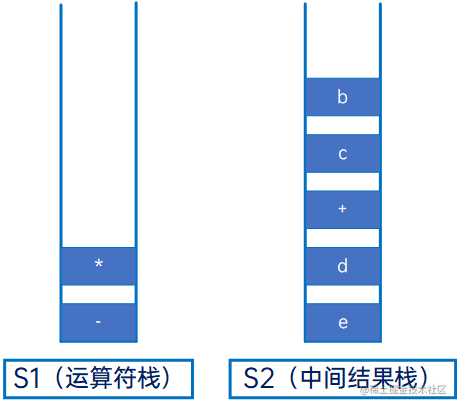
然后是“+”，与S1的栈顶元素“*”比较，优先级较低，因此先将S1的栈顶元素弹出，放到S2：

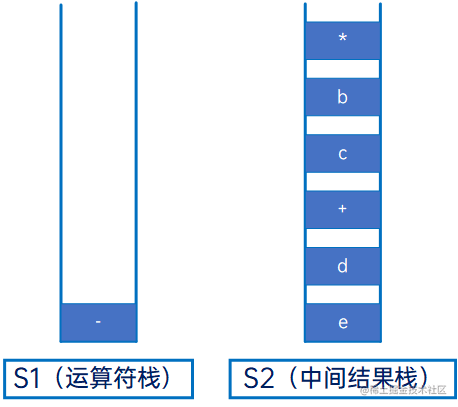
然后与S1新的栈顶元素“-”相比，优先级相同，因此直接将“+”压入S1：

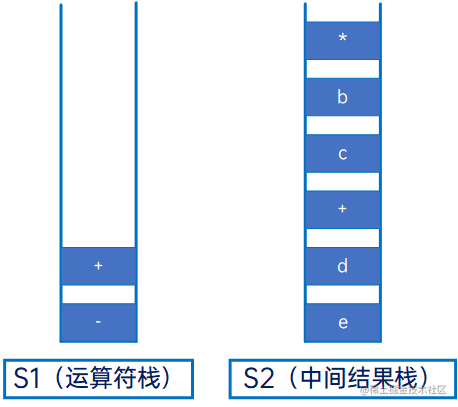
然后是“a”，操作数，直接压入S2：

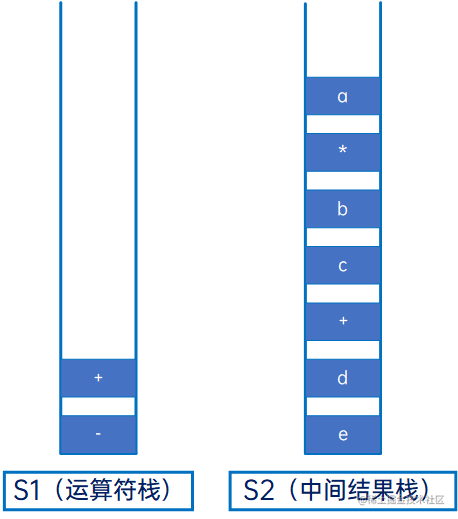
中缀表达式的所有字符都已读取完，这时，将S1的所有元素依次弹出，压入S2：

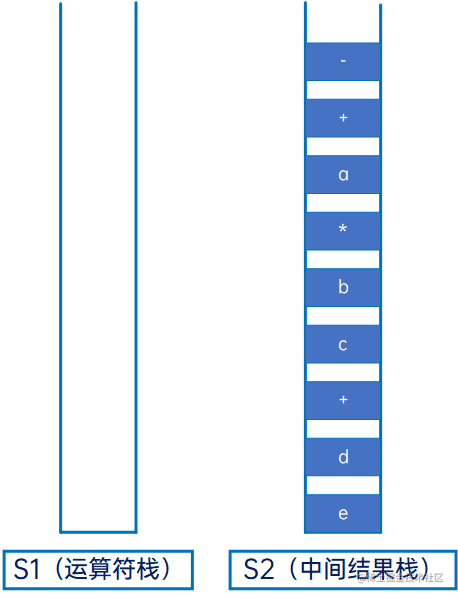
再将S2依次读出，得到前缀表达式结果：

- + a * b c + d e

我们用两栈共享空间的方式来实现代码：


/*** 判断字符串是否是数字** @param val 待判断的字符串* @return 是数字则返回true，否则返回false* @author Korbin* @date 2023-01-16 16:53:26**/
private boolean isData(String val) {Pattern p = Pattern.compile("^[a-zA-Z0-9]+$");return p.matcher(val).find();
}/*** 中缀表达式转前缀表达式** @param infix 中缀表达式* @return 前缀表达式* @author Korbin* @date 2023-01-16 11:49:29**/
public String infix2Prefix(String[] infix) {// 定义一个双向栈// 左边栈为S1，为运算符栈// 右边栈为S2，为中间结果栈BidirectionalStack<String> stack = new BidirectionalStack<>();stack.init(infix.length);for (int i = infix.length - 1; i >= 0; i--) {// 从右至左迭代中缀表达式String curStr = infix[i];// 取出运行符栈的栈顶元素String topOperator = null;try {topOperator = stack.getTop(1);} catch (Exception e) {// do nothing}// 如果为操作数直接入中间结果栈if (isData(curStr)) {// 操作数stack.push(curStr, 2);} else if (curStr.equals("(")) {// 左括号while (null != topOperator && !topOperator.equals(")")) {// 弹出运算符栈的元素，并压入中间结果栈，直到遇到右括号为止stack.push(stack.pop(1), 2);try {topOperator = stack.getTop(1);} catch (Exception e) {// do nothingtopOperator = null;}}if (null != topOperator) {// 抛弃右括号stack.pop(1);}} else if (curStr.equals(")")) {// 右括号// 直接进入运算符栈stack.push(curStr, 1);} else if (curStr.equals("+") || curStr.equals("-") || curStr.equals("*") || curStr.equals("/")) {// 运算符boolean inserted = false;while (!inserted) {if (null == topOperator || topOperator.equals(")")) {// 运算符栈顶为空或栈顶元素为右括号// 直接入栈到运算符栈，并结束stack.push(curStr, 1);inserted = true;} else if (curStr.equals("*") || curStr.equals("/") || topOperator.equals("+") ||topOperator.equals("-")) {// 优先级比栈顶运算符的较高或相等// 即：待比较的字符为乘或除，或者运算符栈顶元素为加或减时// 直接入栈到运算符栈，并结束stack.push(curStr, 1);inserted = true;} else {// 弹出运算符栈的元素，并压入中间结果栈，然后继续比较运算符栈的栈顶元素stack.push(stack.pop(1), 2);try {topOperator = stack.getTop(1);} catch (Exception e) {// do nothingtopOperator = null;}}}} else {// 其他情况，例如为空时，1直接入中间结果栈if (!curStr.equals(" ")) {stack.push(curStr, 2);}}}// 然后将运算符栈中的所有元素再压入中间结果栈while (!stack.isEmpty(1)) {stack.push(stack.pop(1), 2);}// 得到结果StringBuilder result = new StringBuilder();while (!stack.isEmpty(2)) {result.append(stack.pop(2));}return result.toString();}

6.3 中缀表达式转后缀表达式的代码实现

(1) 初始化两个栈：运算符栈S1和储存中间结果的栈S2；

(2) 从左至右扫描中缀表达式；

(3) 遇到操作数时，将其压入S2；

(4) 遇到运算符时，比较其与S1栈顶运算符的优先级：

1) 如果S1为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；

2) 否则，若优先级比栈顶运算符的高，也将运算符压入S1（注意转换为前缀表达式时是优先级较高或相同，而这里则不包括相同的情况）；

3) 否则，将S1栈顶的运算符弹出并压入到S2中，然后取出S1中新的栈顶元素，再次转到(4)进行比较；

(5) 遇到括号时：

1) 如果是左括号“(”，则直接压入S1；

2) 如果是右括号“)”，则依次弹出S1栈顶的运算符，并压入S2，直到遇到左括号为止，此时将这一对括号丢弃；

(6) 重复步骤(2)至(5)，直到表达式的最右边；

(7) 将S1中剩余的运算符依次弹出并压入S2；

(8) 依次弹出S2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式（转换为前缀表达式时不用逆序）。

&msp; 然后以以下表达式为例：

a + b * c - (d + e)

先定义两个空的栈：

然后从头开始迭代，先是“a”，操作数，直接压入S2：

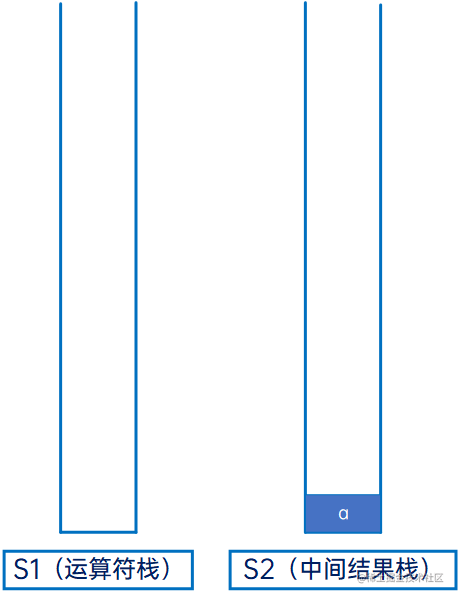
然后是“+”，运算符，与S1的栈顶元素比较，因S1的栈顶元素为空，因此直接压入S1：

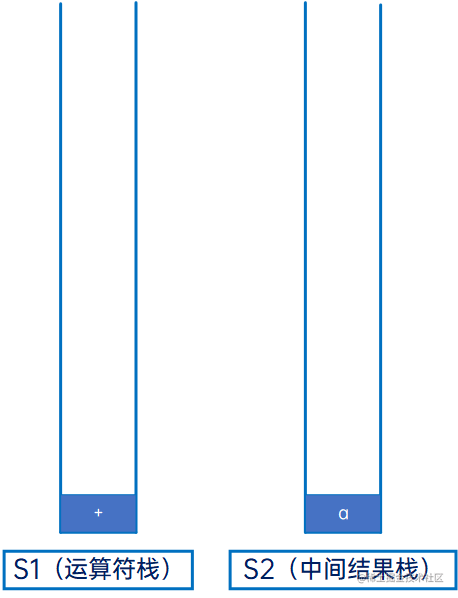
然后是“b”，操作数，直接压入S2：

然后是“*”，运算符，与S1的栈顶元素“+”比较，优先级较高，直接压入S1：

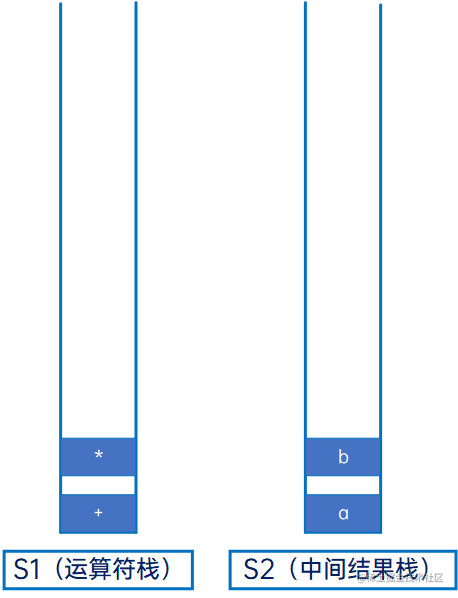
然后是“c”，操作数，直接压入S2：

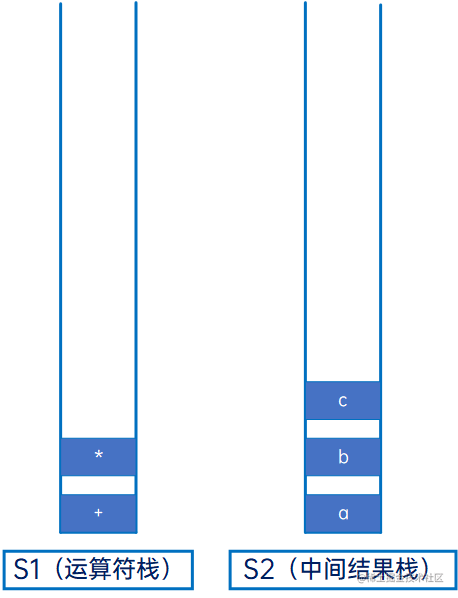
然后是“-”，操作数，与S1的栈顶元素“”比较，发现优先级低，因此将“”从S1弹出，压入S2：

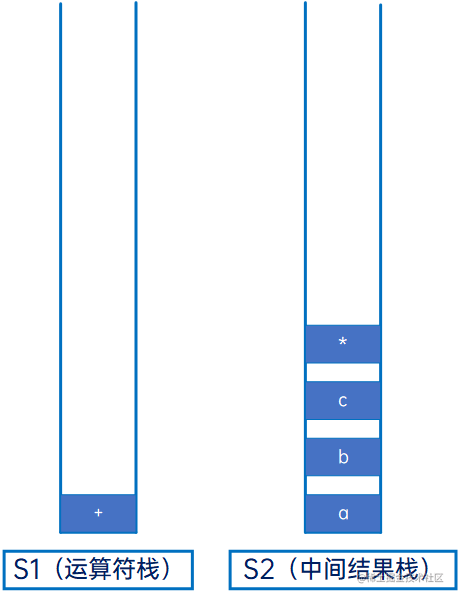
继续与S1新的栈顶元素“+”比较，优先级相同，将“+”从S1弹出，压入S2：

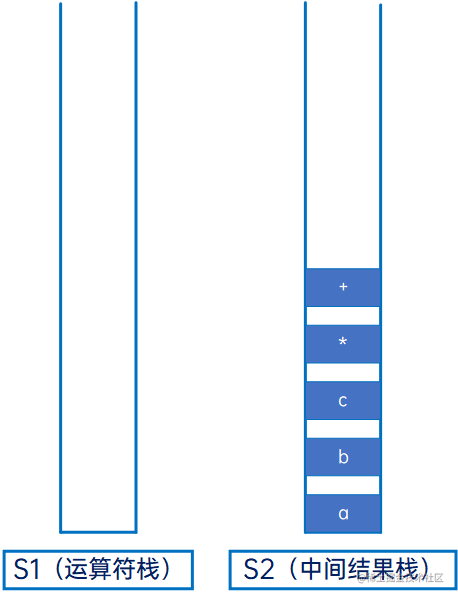
继续与S1新的栈顶元素比较，发现S1为空，因此直接将“-”压入S1：

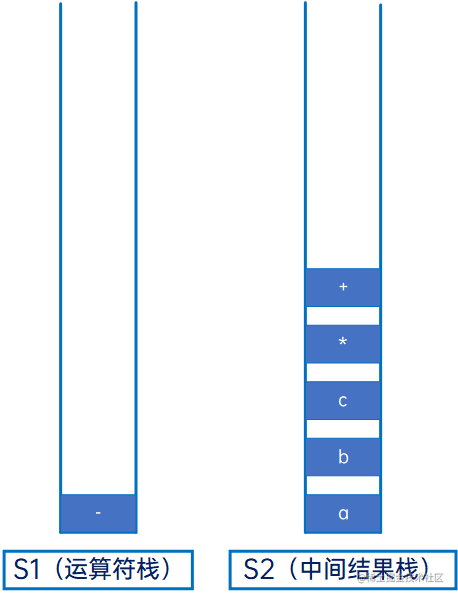
然后是“(”，直接压入S1：

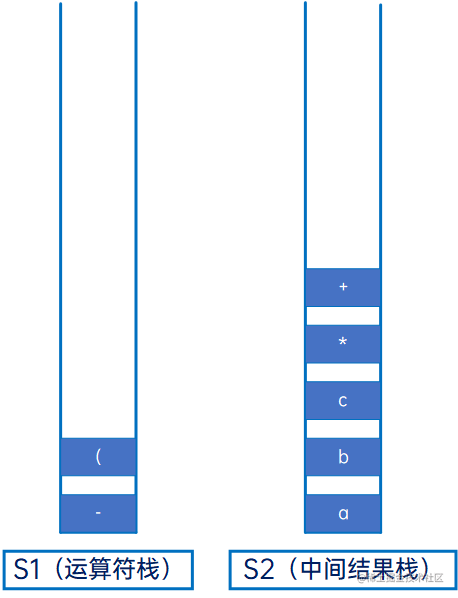
然后是“d”，操作数，直接压入S2：

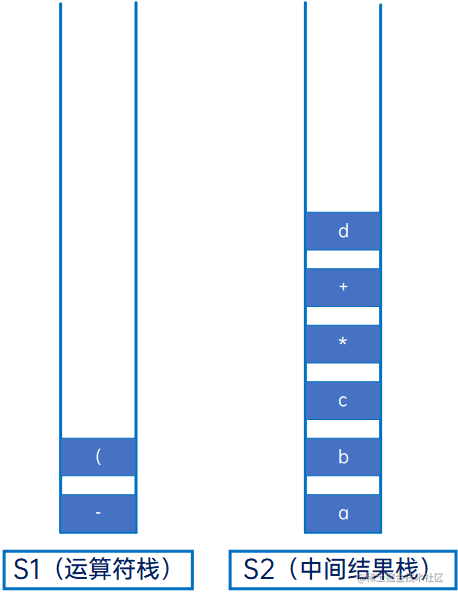
然后是“+”，运算符，与S1的栈顶元素“(”比较，因此是左括号，因此直接压入S1：

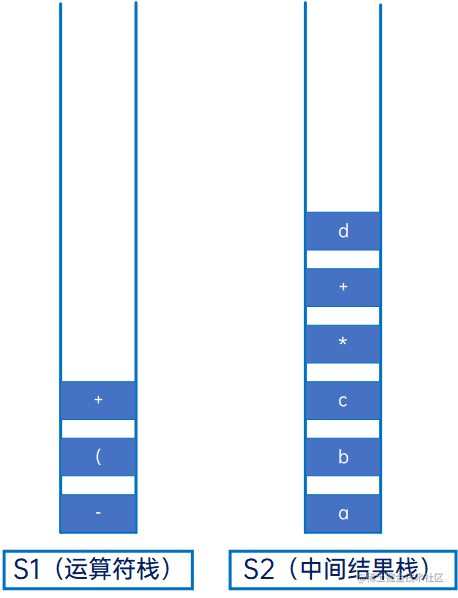
然后是“e”，操作数，直接压入S2：

然后是“)”，依次弹出S1的元素，压入S2，直到遇到左括号，然后把这一对括号去掉：

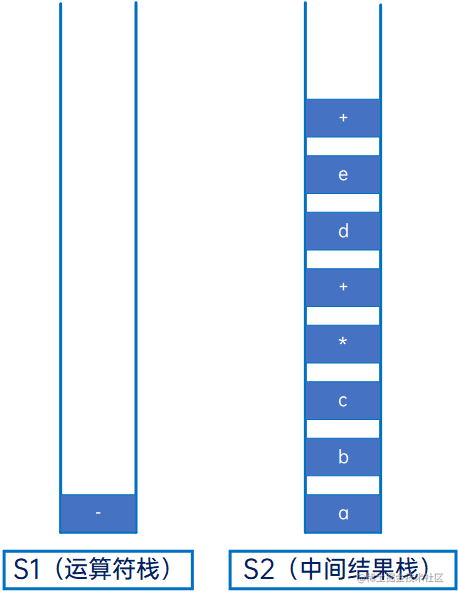
迭代完毕，把S1剩余的元素依次压入S2：

从S2中依次读取出结果：

- + e d + * c b a

reverse，得到后缀表达式结果：

a b c * + d e + -

代码如下所示：

/*** 中缀表达式转后缀表达式** @param infix 后缀表达式* @return 前缀表达式* @author Korbin* @date 2023-01-16 11:49:29**/
public String infix2Suffix(String[] infix) {// 定义一个双向栈// 左边栈为S1，为运算符栈// 右边栈为S2，为中间结果栈BidirectionalStack<String> stack = new BidirectionalStack<>();stack.init(infix.length);for (int i = 0; i <= infix.length - 1; i++) {// 从左至右迭代中缀表达式String curStr = infix[i];// 取出运行符栈的栈顶元素String topOperator = null;try {topOperator = stack.getTop(1);} catch (Exception e) {// do nothing}// 如果为操作数直接入中间结果栈if (isData(curStr)) {// 操作数stack.push(curStr, 2);} else if (curStr.equals("(")) {// 左括号// 直接进入运算符栈stack.push(curStr, 1);} else if (curStr.equals(")")) {// 右括号while (null != topOperator && !topOperator.equals("(")) {// 弹出运算符栈的元素，并压入中间结果栈，直到遇到左括号为止stack.push(stack.pop(1), 2);try {topOperator = stack.getTop(1);} catch (Exception e) {// do nothingtopOperator = null;}}if (null != topOperator) {// 抛弃右括号stack.pop(1);}} else if (curStr.equals("+") || curStr.equals("-") || curStr.equals("*") || curStr.equals("/")) {// 运算符boolean inserted = false;while (!inserted) {if (null == topOperator || topOperator.equals("(")) {// 运算符栈顶为空或栈顶元素为左括号// 直接入栈到运算符栈，并结束stack.push(curStr, 1);inserted = true;} else if ((curStr.equals("*") || curStr.equals("/")) &&(topOperator.equals("+") || topOperator.equals("-"))) {// 优先级比栈顶运算符的较高// 即：运算符栈顶元素为加或减时// 直接入栈到运算符栈，并结束stack.push(curStr, 1);inserted = true;} else {// 弹出运算符栈的元素，并压入中间结果栈，然后继续比较运算符栈的栈顶元素stack.push(stack.pop(1), 2);try {topOperator = stack.getTop(1);} catch (Exception e) {// do nothingtopOperator = null;}}}} else {// 其他情况，例如为空时，1直接入中间结果栈if (!curStr.equals(" ")) {stack.push(curStr, 2);}}}// 然后将运算符栈中的所有元素再压入中间结果栈while (!stack.isEmpty(1)) {stack.push(stack.pop(1), 2);}// 得到结果StringBuilder result = new StringBuilder();while (!stack.isEmpty(2)) {result.append(stack.pop(2));}return result.reverse().toString();
}

6.4 使用前缀表达式计算四则运算

现有四则运算表达式：

9 + (3 - 1) * 3 + 10 / 2

转化成前缀表达式后是：

+ + 9 * - 3 1 3 / 10 2

先初始化一个空栈，然后从右向左开始处理，规则是：如果是数字，则进栈，如果是符号，就将处于栈顶的两个数字出栈，进行运算，运算结果进栈，一直到最终获得结果，注意，栈顶元素是“x”，栈的第二个元素是“y”，则当是运算符“zz”时，运算方式应是“x zz y”。

如上述前缀表达式，先是“2”，直接进栈：

然后是“10”，直接进栈：

然后是“/”，取出栈顶的两个元素，然后进行“10 / 2”处理，得到5，然后入栈：

然后是“3”，直接进栈：

然后是“1”，直接进栈：

然后是“3”，直接进栈：

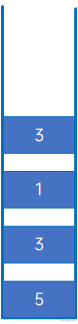
然后是“-”，取出栈顶的两个元素，进行“3 - 1”处理，得到2，然后入栈：

然后是“*”，取出栈顶的两个元素，进行“2 * 3”处理，得到6，然后入栈：

然后是“9”，直接进栈：

然后是“+”，取出栈顶的两个元素，进行“9 + 6”处理，得到15，然后入栈：

然后是“+”，取出栈顶的两个元素，进行“15 + 5”处理，得到20，然后入栈：

于是得到最终结果20。

代码如下所示：

/*** 使用前缀表达式计算** @param prefixExpression 前缀表达式* @return 计算结果* @author Korbin* @date 2023-01-16 18:17:01**/
public double prefixCalc(String[] prefixExpression) {LinkStack<String> stack = new LinkStack<>();int length = prefixExpression.length;for (int i = length - 1; i >= 0; i--) {String curStr = prefixExpression[i];if (isData(curStr)) {// 如果是操作数，则直接入栈stack.push(curStr);} else {// 否则，使用第二个元素 运算符 栈顶元素得出结果后，再将结果入栈double firstData = Double.parseDouble(stack.pop().getData());double secondData = Double.parseDouble(stack.pop().getData());double value = 0;switch (curStr) {case "+":value = firstData + secondData;break;case "-":value = firstData - secondData;break;case "*":value = firstData * secondData;break;case "/":value = firstData / secondData;break;}stack.push(String.valueOf(value));}}return Double.parseDouble(stack.pop().getData());
}

6.5 使用后缀表达式计算四则运算

现有四则运算表达式：

9 + (3 - 1) * 3 + 10 / 2

转化成后缀表达式后是：

9 3 1 - 3 * + 10 2 / +

先初始化一个空栈，然后从左向右开始处理，规则是：如果是数字，则进栈，如果是符号，就将处于栈顶的两个数字出栈，进行运算，运算结果进栈，一直到最终获得结果，注意，栈顶元素是“x”，栈的第二个元素是“y”，则当是运算符“zz”时，运算方式应是“y zz x”。

如上述后缀表达式，先是“9”，直接进栈：

然后是“3”，直接进栈：

然后是“1”，直接进栈：

然后是“-”，取出栈顶的两个值，进行“3 - 1”处理，得到2，再进栈：

然后是“3”，直接进栈：

然后是“*”，取出栈顶的两个值，进行“2 * 3”处理，得到6，再进栈：

然后是“+”，取出栈顶的两个值，进行“9 + 6”处理，得到15，再进栈：

然后是“10”，直接进栈：

然后是“2”，直接进栈：

然后是“/”，取出栈顶的两个值，进行“10 / 2”处理，得到5，再进栈：

然后是“+”，取出栈顶的两个值，进行“15 + 5”处理，得到20，再进栈：

这样就得到了最终结果。

代码如下所示：

/*** 使用后缀表达式计算** @param suffixExpression 后缀表达式* @return 计算结果* @author Korbin* @date 2023-01-16 18:17:01**/
public double suffixCalc(String[] suffixExpression) {LinkStack<String> stack = new LinkStack<>();int length = suffixExpression.length;for (int i = 0; i <= length - 1; i++) {String curStr = suffixExpression[i];if (isData(curStr)) {// 如果是操作数，则直接入栈stack.push(curStr);} else {// 否则，使用栈顶元素 运算符 第二个元素得出结果后，再将结果入栈double secondData = Double.parseDouble(stack.pop().getData());double firstData = Double.parseDouble(stack.pop().getData());double value = 0;switch (curStr) {case "+":value = firstData + secondData;break;case "-":value = firstData - secondData;break;case "*":value = firstData * secondData;break;case "/":value = firstData / secondData;break;}stack.push(String.valueOf(value));}}return Double.parseDouble(stack.pop().getData());
}