螺旋矩阵算法(leetcode第59题)
题目描述:
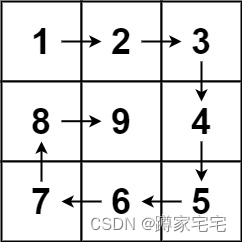
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。示例 1:输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:输入:n = 1
输出:[[1]]提示:1 <= n <= 20算法:
思路:
设定四个边界,每次输出完一行或者一列,就移动边界,直到边界相碰
代码实现:
/*** Return an array of arrays of size *returnSize.* The sizes of the arrays are returned as *returnColumnSizes array.* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().*/
# include<stdio.h>
# include<stdlib.h>
int** generateMatrix(int n, int* returnSize, int** returnColumnSizes) {*returnSize=n;//行空间*returnColumnSizes=(int*)malloc(n*sizeof(int));//行空间for(int i=0;i<n;i++) (*returnColumnSizes)[i]=n;//列空间int **matrix=(int**)malloc(n*sizeof(int*));for(int i=0;i<n;i++){matrix[i]=(int*)malloc(sizeof(int)*n);}int num=1;//四个边界值int right=n-1,left=0,up=0,down=n-1;//条件:不超过边界 or num不超过n^2while(up<=down && left<=right){ //up<=down && left<=right 或 num<=n*nfor(int i=left;i<=right;i++) matrix[up][i]=num++;up++;//上边界下移for(int i=up;i<=down;i++) matrix[i][right]=num++;right--;//右边界左移for(int i=right;i>=left;i--) matrix[down][i]=num++;down--;//下边界上移for(int i=down;i>=up;i--) matrix[i][left]=num++;left++;//左边界右移}return matrix;
}