[足式机器人]Part2 Dr. CAN学习笔记-数学基础Ch0-5Laplace Transform of Convolution卷积的拉普拉斯变换
本文仅供学习使用
本文参考:
B站:DR_CAN
Dr. CAN学习笔记-数学基础Ch0-5Laplace Transform of Convolution卷积的拉普拉斯变换
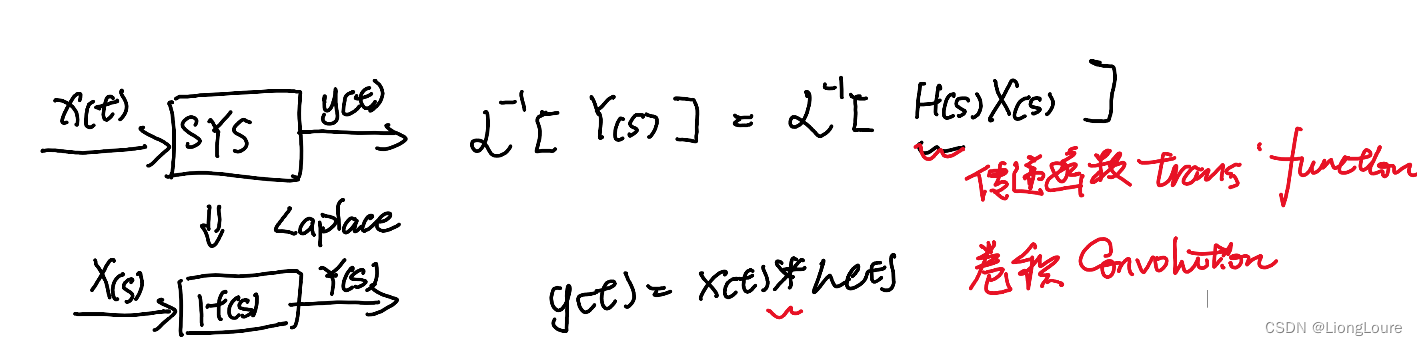
Laplace Transform : X ( s ) = L [ x ( t ) ] = ∫ 0 ∞ x ( t ) e − s t d t X\left( s \right) =\mathcal{L} \left[ x\left( t \right) \right] =\int_0^{\infty}{x\left( t \right) e^{-st}}\mathrm{d}t X(s)=L[x(t)]=∫0∞x(t)e−stdt
Convolution : x ( t ) ∗ g ( t ) = ∫ 0 t x ( τ ) g ( t − τ ) d τ x\left( t \right) *g\left( t \right) =\int_0^t{x\left( \tau \right) g\left( t-\tau \right)}\mathrm{d}\tau x(t)∗g(t)=∫0tx(τ)g(t−τ)dτ
证明: L [ x ( t ) ∗ g ( t ) ] = X ( s ) G ( s ) \mathcal{L} \left[ x\left( t \right) *g\left( t \right) \right] =X\left( s \right) G\left( s \right) L[x(t)∗g(t)]=X(s)G(s)
L [ x ( t ) ∗ g ( t ) ] = ∫ 0 ∞ ∫ 0 t x ( τ ) g ( t − τ ) d τ e − s t d t = ∫ 0 ∞ ∫ τ ∞ x ( τ ) g ( t − τ ) e − s t d t d τ \mathcal{L} \left[ x\left( t \right) *g\left( t \right) \right] =\int_0^{\infty}{\int_0^t{x\left( \tau \right) g\left( t-\tau \right) \mathrm{d}\tau}e^{-st}}\mathrm{d}t=\int_0^{\infty}{\int_{\tau}^{\infty}{x\left( \tau \right) g\left( t-\tau \right)}e^{-st}}\mathrm{d}t\mathrm{d}\tau L[x(t)∗g(t)]=∫0∞∫0tx(τ)g(t−τ)dτe−stdt=∫0∞∫τ∞x(τ)g(t−τ)e−stdtdτ
>令: u = t − τ , t = u + τ , d t = d u + d τ , t ∈ [ τ , + ∞ ) ⇒ u ∈ [ 0 , + ∞ ) u=t-\tau ,t=u+\tau ,\mathrm{d}t=\mathrm{d}u+\mathrm{d}\tau ,t\in \left[ \tau ,+\infty \right) \Rightarrow u\in \left[ 0,+\infty \right) u=t−τ,t=u+τ,dt=du+dτ,t∈[τ,+∞)⇒u∈[0,+∞)
L [ x ( t ) ∗ g ( t ) ] = ∫ 0 ∞ ∫ 0 ∞ x ( τ ) g ( u ) e − s ( u + τ ) d u d τ = ∫ 0 ∞ x ( τ ) e − s τ d τ ∫ 0 ∞ g ( u ) e − s u d u = X ( s ) G ( s ) \mathcal{L} \left[ x\left( t \right) *g\left( t \right) \right] =\int_0^{\infty}{\int_0^{\infty}{x\left( \tau \right) g\left( u \right)}e^{-s\left( u+\tau \right)}}\mathrm{d}u\mathrm{d}\tau =\int_0^{\infty}{x\left( \tau \right)}e^{-s\tau}\mathrm{d}\tau \int_0^{\infty}{g\left( u \right)}e^{-su}\mathrm{d}u=X\left( s \right) G\left( s \right) L[x(t)∗g(t)]=∫0∞∫0∞x(τ)g(u)e−s(u+τ)dudτ=∫0∞x(τ)e−sτdτ∫0∞g(u)e−sudu=X(s)G(s)
L [ x ( t ) ∗ g ( t ) ] = L [ x ( t ) ] L [ g ( t ) ] = X ( s ) G ( s ) \mathcal{L} \left[ x\left( t \right) *g\left( t \right) \right] =\mathcal{L} \left[ x\left( t \right) \right] \mathcal{L} \left[ g\left( t \right) \right] =X\left( s \right) G\left( s \right) L[x(t)∗g(t)]=L[x(t)]L[g(t)]=X(s)G(s)
