王道数据结构课后代码题 p149 第8—— 12(c语言代码实现)
目录
8.假设二叉树采用二叉链表存储结构存储,试设计一个算法,计算一棵给定二叉树的所有双分支结点个数。
9.设树B是一棵采用链式结构存储的二叉树,编写一个把树 B中所有结点的左、右子树进行交换的函数。
10.假设二叉树采用二叉链存储结构存储,设计一个算法,求先序遍历序列中第 k(1<=k<=二叉树中结点个数)个结点的值
11.已知二叉树以二叉链表存储,编写算法完成: 对于树中每个元素值为X 的结点,删去以它为根的子树,并释放相应的空间。
12.在二叉树中查找值为 x 的结点,试编写算法(用 C语言)打印值为x的结点的所有祖先,假设值为X的结点不多于一个。
8.假设二叉树采用二叉链表存储结构存储,试设计一个算法,计算一棵给定二叉树的所有双分支结点个数。
本题代码如下
int twonode(tree t)
{if (t == NULL)//若为空树return 0;else if (t->lchild&& t->rchild)//双分支结点return twonode(t->lchild) + twonode(t->rchild) + 1;else//单分支或叶子节点return twonode(t->lchild) + twonode(t->rchild);
}完整测试代码
#include<stdio.h>
#include<stdlib.h>
#define true 1
#define false 0
typedef struct treenode
{char data;struct treenode* lchild, * rchild;
}treenode,*tree;
void buildtree(tree* t)
{char ch;ch = getchar();if (ch == '#')*t=NULL;else{*t = (treenode*)malloc(sizeof(treenode));(*t)->data = ch;buildtree(&((*t)->lchild));buildtree(&((*t)->rchild));}
}
int twonode(tree t)
{if (t == NULL)//若为空树return 0;else if (t->lchild&& t->rchild)//双分支结点return twonode(t->lchild) + twonode(t->rchild) + 1;else//单分支或叶子节点return twonode(t->lchild) + twonode(t->rchild);
}
int main()
{tree t;buildtree(&t);printf("双支数为%d\n",twonode(t));return 0;
}用ABD##E##CF##G##这个测试
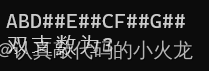
9.设树B是一棵采用链式结构存储的二叉树,编写一个把树 B中所有结点的左、右子树进行交换的函数。
本题代码如下
void swap(tree* t)
{if (*t){treenode* temp = (*t)->lchild;(*t)->lchild = (*t)->rchild;(*t)->rchild = temp;swap(&(*t)->lchild);swap(&(*t)->rchild);}
}完整测试代码
#include<stdio.h>
#include<stdlib.h>
typedef struct treenode
{char data;struct treenode* lchild, * rchild;
}treenode,*tree;
void buildtree(tree* t)
{char ch;ch = getchar();if (ch =='#')*t = NULL;else{*t = (treenode*)malloc(sizeof(treenode));(*t)->data = ch;buildtree(&((*t)->lchild));buildtree(&((*t)->rchild));}
}
void swap(tree* t)
{if (*t){treenode* temp = (*t)->lchild;(*t)->lchild = (*t)->rchild;(*t)->rchild = temp;swap(&(*t)->lchild);swap(&(*t)->rchild);}
}
void disp(tree* t)
{if (*t){printf("%c", (*t)->data);disp(&(*t)->lchild);disp(&(*t)->rchild);}
}
int main()
{tree t;buildtree(&t);printf("交换过后的二叉树为(前序序列):");swap(&t);disp(&t);return 0;
}用ABD##E##CF##G##测试

10.假设二叉树采用二叉链存储结构存储,设计一个算法,求先序遍历序列中第 k(1<=k<=二叉树中结点个数)个结点的值
本题代码如下
// 查找第k个节点值的函数
char serchk(tree* t, int k)
{if (*t == NULL) // 如果节点为空,返回'*'表示未找到return '*';if (i == k) // 如果当前节点是第k个节点,返回节点数据return (*t)->data;i++; // 更新当前节点位置char s = serchk(&(*t)->lchild, k); // 递归查找左子树中的第k个节点if (s != '*') // 如果左子树中找到,直接返回结果return s;s = serchk(&(*t)->rchild, k); // 否则递归查找右子树中的第k个节点return s; // 返回查找结果
}完整测试代码
#include<stdio.h>// 定义二叉树节点结构体
typedef struct treenode
{char data; // 节点存储的数据struct treenode* lchild, * rchild; // 左右子节点指针
}treenode,*tree;// 构建二叉树函数
void buildtree(tree* t)
{char ch;ch = getchar(); // 从输入中读取一个字符if (ch == '#') // 如果字符为'#',表示空节点*t = NULL;else{*t = (treenode*)malloc(sizeof(treenode)); // 分配内存空间给新节点(*t)->data = ch; // 将读取到的字符赋值给节点数据(*t)->lchild = NULL; // 初始化左子节点为空(*t)->rchild = NULL; // 初始化右子节点为空buildtree(&(*t)->lchild); // 递归构建左子树buildtree(&(*t)->rchild); // 递归构建右子树}
}int i = 1; // 全局变量,用于记录当前遍历的节点位置// 查找第k个节点值的函数
char serchk(tree* t, int k)
{if (*t == NULL) // 如果节点为空,返回'*'表示未找到return '*';if (i == k) // 如果当前节点是第k个节点,返回节点数据return (*t)->data;i++; // 更新当前节点位置char s = serchk(&(*t)->lchild, k); // 递归查找左子树中的第k个节点if (s != '*') // 如果左子树中找到,直接返回结果return s;s = serchk(&(*t)->rchild, k); // 否则递归查找右子树中的第k个节点return s; // 返回查找结果
}int main()
{tree t; // 定义二叉树变量tbuildtree(&t); // 构建二叉树char f=serchk(&t, 5); // 查找第5个节点的值printf("%c", f); // 输出查找结果return 0;
}
用ABD##E##CF##G##测试

11.已知二叉树以二叉链表存储,编写算法完成: 对于树中每个元素值为X 的结点,删去以它为根的子树,并释放相应的空间。
可以直接使用前序遍历,访问到值为x的结点,就递归的删除它的左、右子树。
本题代码如下
void release(tree* t)//递归释放结点
{if (!*t)return;release(&(*t)->lchild);release(&(*t)->rchild);free(*t);
}
void deletex(tree* t,char x)
{if (*t == NULL)return;if((*t)->data==x){release(t);*t = NULL;}if (*t != NULL)//前序遍历的去找{deletex(&(*t)->lchild, x);deletex(&(*t)->rchild, x);}
}完整测试代码
#include<stdio.h>
#include<stdlib.h>
typedef struct treenode
{char data;struct treenode* lchild, * rchild;
}treenode,*tree;
void buildtree(tree* t)
{char ch;ch = getchar();if (ch == '#')*t = NULL;else{*t = (treenode*)malloc(sizeof(treenode));(*t)->data = ch;buildtree(&(*t)->lchild);buildtree(&(*t)->rchild);}
}
void release(tree* t)
{if (!*t)return;release(&(*t)->lchild);release(&(*t)->rchild);free(*t);
}
void deletex(tree* t,char x)
{if (*t == NULL)return;if((*t)->data==x){release(t);*t = NULL;}if (*t != NULL){deletex(&(*t)->lchild, x);deletex(&(*t)->rchild, x);}
}
void disp(tree* t)
{if (*t){printf("%c", (*t)->data);disp(&(*t)->lchild);disp(&(*t)->rchild);}
}
int main()
{tree t;buildtree(&t);deletex(&t, 'C');disp(&t);return 0;
}用ABD##E##CF##G##测试
/* A
B C
D E F G */

12.在二叉树中查找值为 x 的结点,试编写算法(用 C语言)打印值为x的结点的所有祖先,假设值为X的结点不多于一个。
采用非递归后序遍历,最后访问根结点,访问到值为 x 的结点时,栈中所有元素均为该结点的祖先,依次出栈打印.
本题代码如下(注释详解)
// 寻找指定字符的所有祖先结点
void ancestor(tree* t, char x)
{stack s[10]; // 定义一个大小为10的栈,用于存储二叉树的结点指针和标记位 int top = -1; // 初始化栈顶为-1,表示栈为空 while (*t != NULL || top != -1) // 当当前节点非空或者栈非空时,继续循环 {while (*t != NULL) // 当当前结点非空时,将其入栈并向左子树遍历 {top++;s[top].t = *t; // 将当前结点入栈 s[top].tag = 0; // 标记位设为0,表示该结点尚未被访问过 *t = (*t)->lchild; // 向左子树遍历 }while (top != -1 && s[top].tag == 1) // 当栈非空且栈顶元素的标记位为1时,出栈(即回退) {top--;}if (top != -1) // 当栈非空时,进行以下操作 {if (s[top].t->data == x) // 如果栈顶元素的data字段等于指定字符x,则输出所有祖先结点 {printf("所有的祖先结点为:\n");for (int i = 0; i < top; i++) // 遍历栈中所有元素(不包括栈顶元素)并输出其data字段 {printf("%c ", s[i].t->data);}break; // 找到指定字符的所有祖先结点后,跳出循环 }s[top].tag = 1; // 如果栈顶元素的data字段不等于指定字符x,将其标记位设为1,表示该结点已经被访问过 *t = s[top].t->rchild; // 向右子树遍历 }}
}完整测试代码
#include<stdio.h>
#include<stdlib.h>
// 定义一个二叉树结点
typedef struct treenode
{char data; //结点存储的数据 struct treenode* lchild, * rchild; // 结点的左右孩子
} treenode, * tree;
// 定义一个栈结构
typedef struct
{treenode* t; // 栈中存储的是二叉树的结点指针 int tag; // 标记位,主要用于记录结点是否已经被访问过
} stack;
// 建立二叉树
void buildtree(tree* t)
{char ch;ch = getchar(); // 从标准输入获取一个字符 if (ch == '#') // 如果输入的是'#',则该节点为空 *t = NULL;else{*t = (treenode*)malloc(sizeof(treenode)); // 为新的结点分配内存空间 (*t)->data = ch; // 将输入的字符赋值给节点的data字段 (*t)->lchild = NULL; // 初始化结点的左右孩子为空 (*t)->rchild = NULL;buildtree(&(*t)->lchild); // 递归建立左子树 buildtree(&(*t)->rchild); // 递归建立右子树 }
}
// 寻找指定字符的所有祖先结点
void ancestor(tree* t, char x)
{stack s[10]; // 定义一个大小为10的栈,用于存储二叉树的结点指针和标记位 int top = -1; // 初始化栈顶为-1,表示栈为空 while (*t != NULL || top != -1) // 当当前节点非空或者栈非空时,继续循环 {while (*t != NULL) // 当当前结点非空时,将其入栈并向左子树遍历 {top++;s[top].t = *t; // 将当前结点入栈 s[top].tag = 0; // 标记位设为0,表示该结点尚未被访问过 *t = (*t)->lchild; // 向左子树遍历 }while (top != -1 && s[top].tag == 1) // 当栈非空且栈顶元素的标记位为1时,出栈(即回退) {top--;}if (top != -1) // 当栈非空时,进行以下操作 {if (s[top].t->data == x) // 如果栈顶元素的data字段等于指定字符x,则输出所有祖先结点 {printf("所有的祖先结点为:\n");for (int i = 0; i < top; i++) // 遍历栈中所有元素(不包括栈顶元素)并输出其data字段 {printf("%c ", s[i].t->data);}break; // 找到指定字符的所有祖先结点后,跳出循环 }s[top].tag = 1; // 如果栈顶元素的data字段不等于指定字符x,将其标记位设为1,表示该结点已经被访问过 *t = s[top].t->rchild; // 向右子树遍历 }}
}
int main()
{tree t; // 定义一个二叉树节点指针t buildtree(&t); // 建立二叉树 ancestor(&t, 'D'); // 找出字符'D'的所有祖先结点并输出 return 0;
}用ABD##E##CF##G##测试
/* A
B C
D E F G */

