SimplePIR——目前最快单服务器匿踪查询方案
一、介绍
这篇论文旨在实现高效的单服务器隐私信息检索(PIR)方案,以解决在保护用户隐私的同时快速检索数据库的问题。为了实现这一目标,论文提出了两种新的PIR方案:SimplePIR和DoublePIR。这两种方案的实现基于学习与错误假设,并在保持高吞吐量的同时显著降低了客户端的通信成本。SimplePIR实现了每核心10 GB/s的服务器吞吐量,接近内存带宽,但需要客户端下载一个相对较大的“提示”。DoublePIR方案通过递归地使用SimplePIR,以更低的通信成本获取所需的数据库记录。这些方案的突破点在于在保持高吞吐量的同时,显著降低了客户端的通信成本,填补了单服务器PIR方案设计空间中的一些空白。通过这些创新,论文为单服务器PIR方案的设计和实现提供了新的思路和解决方案。
二、背景知识
1.Learning with errors (LWE)
是一种基于格的加密技术,它是一种在计算上难以解决的问题。LWE问题的基本形式是:给定一个由n个向量组成的矩阵A和一个向量b,以及一个小的误差向量e,找到一个向量s,使得As+e=b。LWE问题的难度在于,对于给定的A和b,找到s是困难的,因为误差向量e是随机的。LWE问题是一种基础的加密原语,可以用于构建各种加密方案,包括私有信息检索(PIR)方案。在本文中,SimplePIR方案的安全性基于LWE假设,即LWE问题的解决难度足以保证SimplePIR方案的安全性。在文字提及到(𝑛, 𝑞, 𝜒)-LWE,解释一下:𝑛代表向量的维度,𝑞代表整数模数,𝜒代表误差分布。因此,(𝑛, 𝑞, 𝜒)-LWE问题描述了在给定向量维度𝑛、整数模数𝑞和误差分布𝜒的情况下,解决Learning with errors (LWE)问题的难度。这种参数化的LWE问题在密码学中具有重要意义,因为不同的参数取值可以导致不同难度的LWE问题,从而影响基于LWE问题构建的加密方案的安全性。因此,对于给定的𝑛、𝑞和𝜒,(𝑛, 𝑞, 𝜒)-LWE问题的难度可以用来评估基于LWE假设的加密方案的安全性
Secret-key Regev encryption:是一种基于LWE假设的加密方案,由Regev在2005年提出。该方案的安全性基于LWE问题的困难性,即在给定矩阵A和向量b的情况下,找到向量s是困难的,其中b是由A和s的点积加上一个小的误差向量e得到的。Secret-key Regev encryption方案的基本思想是将明文编码为一个向量,并将其与一个随机向量的点积加上一个小的误差向量,然后将其加密。具体来说:

详细学习:格密码学与LWE问题
三、算法
1.simplePIR

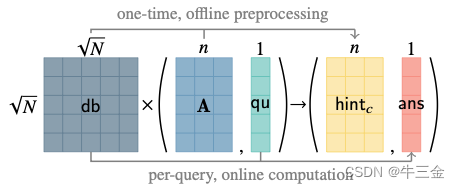
接下来以一种更易理解的方式,我们从一个公式出发:
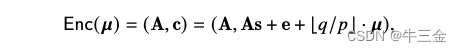
这个公式就是对于刚才理想问题的抽象,其中A是公钥,c是获得的密文,u是待加密的明文,这里需要注意的是u已经从一个数,变成一个向量,其正确性可以使用相同方式证明,u=c·s-A。
接下来我们将公式和图对应起来,A就对应图中A矩阵,c对应图中qu。这样解密计算就相当于ans·s-hintc = D·(cs-A) =D·u,我们这里知道是一个唯“1”向量,相当于获得了D的其中一列的数据。
在文中也说明了这种方式将获得其中一列的数据。至于详细的推导可以查看论文最后的证明。

2.DoublePIR
SimplePIR具有高的服务器端吞吐量,但需要客户端下载和存储一个相对较大的预处理提示,其大小大约为 𝑛√𝑁,其中 𝑛 大约为 210,数据库大小为 𝑁。然后介绍了DoublePIR,这是一种新的PIR方案,它通过递归应用SimplePIR来将提示大小减小到大约 𝑛2,这与数据库大小无关,同时保持服务器端吞吐量高达7.4 GB/s。在实践中,对于一个字节的记录,这个提示大小为16 MB。对于记录非常多的数据库(𝑁 ≫ 𝑛2 ≈ 220),DoublePIR的提示大小比SimplePIR要小得多。与SimplePIR一样,DoublePIR的每个查询的通信成本在数据库大小 𝑁 上是 𝑂 (√𝑁)。

这个推到起来较为复杂,可以参考后面的证明,不做赘述。
四、性能
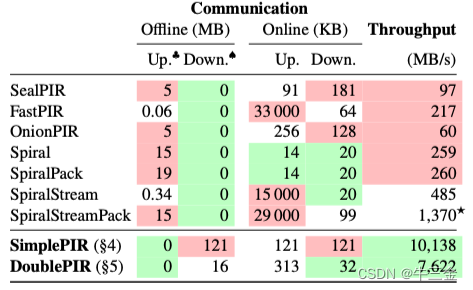
在实际测试中,发现该方案在相同条件下的确能比sealpir性能提升数倍不止。
