AcWing算法提高课-3.1.3香甜的黄油
宣传一下算法提高课整理 <—
CSDN个人主页:更好的阅读体验 <—

题目传送门点这里
题目描述
农夫John发现了做出全威斯康辛州最甜的黄油的方法:糖。
把糖放在一片牧场上,他知道 N 只奶牛会过来舔它,这样就能做出能卖好价钱的超甜黄油。
当然,他将付出额外的费用在奶牛上。
农夫John很狡猾,就像以前的巴甫洛夫,他知道他可以训练这些奶牛,让它们在听到铃声时去一个特定的牧场。
他打算将糖放在那里然后下午发出铃声,以至他可以在晚上挤奶。
农夫John知道每只奶牛都在各自喜欢的牧场(一个牧场不一定只有一头牛)。
给出各头牛在的牧场和牧场间的路线,找出使所有牛到达的路程和最短的牧场(他将把糖放在那)。
数据保证至少存在一个牧场和所有牛所在的牧场连通。
输入格式
第一行: 三个数:奶牛数 N,牧场数 P,牧场间道路数 C。
第二行到第 N+1 行: 1 到 N 头奶牛所在的牧场号。
第 N+2 行到第 N+C+1 行:每行有三个数:相连的牧场A、B,两牧场间距 D,当然,连接是双向的。
输出格式
共一行,输出奶牛必须行走的最小的距离和。
数据范围
1≤N≤500,1≤N≤500,1≤N≤500,
2≤P≤800,2≤P≤800,2≤P≤800,
1≤C≤1450,1≤C≤1450,1≤C≤1450,
1≤D≤2551≤D≤2551≤D≤255
样例输入
3 4 5
2
3
4
1 2 1
1 3 5
2 3 7
2 4 3
3 4 5
样例输出
8
思路
本题可以先枚举黄油的位置,再用 spfa 求出每个牧场到当前位置的最短路。
-
这道题不是每个牧场一个奶牛,一个牧场可能有好几个奶牛
-
于是,我们用 cntcntcnt 数组来存第 iii 个仓库有几个奶牛
-
第 iii 个牧场的奶牛路程就是 di×cntid_i×cnt_idi×cnti
····························································································
-
题目中说:数据保证至少存在一个牧场和所有牛所在的牧场连通
-
但是,没有奶牛的牧场虽然有可能贡献答案,也有可能不与有奶牛的牧场连通
-
所以枚举起点时要注意牧场之间的连通性
算法时间复杂度
复杂度为 O(nm)O(nm)O(nm),可以过
本题使用STL中的queue时间上会慢一点,不过不影响AC
这里贴上提交记录:
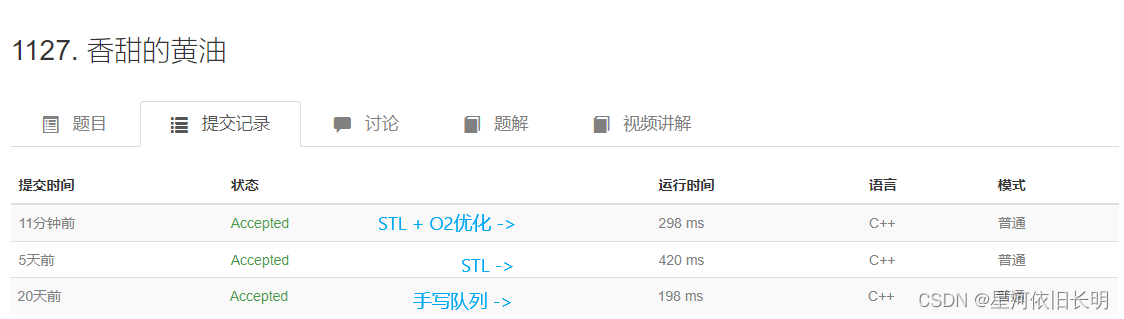
可以看到,queue即使加了O2,效率也比不上手写队列。
所以考试能手写就别用STL,除非你的时间限制很充裕。
AC Code
C++C++C++
#include <iostream>
#include <cstring>using namespace std;typedef pair<int, int> PII;const int N = 810, M = 3010;
const int INF = 0x3f3f3f3f;int n, m, p;
int id[N];
int h[N], e[M], w[M], ne[M], idx;
int q[N], dist[N];
bool st[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}int spfa(int S)
{memset(dist, 0x3f, sizeof(dist));dist[S] = 0;int hh = 0, tt = 1;q[0] = S, st[S] = 1;while (hh != tt){int t = q[hh ++ ];if (hh == N) hh = 0;st[t] = 0;for (int i = h[t]; i != -1; i = ne[i]){int j = e[i];if (dist[j] > dist[t] + w[i]){dist[j] = dist[t] + w[i];if (!st[j]){q[tt ++ ] = j;if (tt == N) tt = 0;st[j] = 1;}}}}int res = 0;for (int i = 0; i < n; i ++ ){int j = id[i];if (dist[j] == INF) return INF;res += dist[j];}return res;
}int main()
{memset(h, -1, sizeof h);scanf("%d%d%d", &n, &p, &m);for (int i = 0; i < n; i ++ )scanf("%d", &id[i]);for (int i = 0; i < m; i ++ ){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c), add(b, a, c);}int res = INF;for (int i = 1; i <= p; i ++ )res = min(res, spfa(i));printf("%d\n", res);return 0;
}

最后,如果觉得对您有帮助的话,点个赞再走吧!
