计算两个结构的差
平面上有6个点,以6a1的方式运动
| 1 | 1 | 1 |
| 1 | - | - |
| - | 1 | - |
| - | - | 1 |
现在有一个点逃逸,剩下的5个点将如何运动?
| 2 | 2 | 2 |
| 3 | - | - |
| - | 3 | - |
| - | - | 3 |
将6a1的6个点减去1个点,只有两种可能,或者变成5a2,或者变成5a3,二者比例是1:1
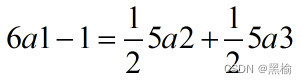
所以这平面上的6个点,在一个点飞出的瞬间,剩下的5个点运动方式只能有两种可能。
算第二种可能,如果同时飞出2个点
| 4a7 | 2a3 | |||||||||
| 1 | 1 | 1 | - | 1 | - | 1 | 1 | - | ||
| 1 | - | - | = | - | 1 | - | + | - | - | - |
| - | 1 | - | 1 | - | - | - | - | - | ||
| - | - | 1 | - | - | 1 | - | - | - | ||
| 4a1 | 2a1 | |||||||||
| 1 | 1 | 1 | - | 1 | 1 | 1 | - | - | ||
| 1 | - | - | = | - | 1 | - | + | 1 | - | - |
| - | 1 | - | - | - | 1 | - | - | - | ||
| - | - | 1 | - | - | - | - | - | - | ||
| 4a2 | 2a2 | |||||||||
| 1 | 1 | 1 | - | 1 | 1 | 1 | - | - | ||
| 1 | - | - | = | - | - | 1 | + | - | 1 | - |
| - | 1 | - | 1 | - | - | - | - | - | ||
| - | - | 1 | - | - | - | - | - | - | ||
| 4a4 | 2a2 | |||||||||
| 1 | 1 | 1 | - | - | 1 | 1 | - | - | ||
| 1 | - | - | = | 1 | 1 | 1 | + | - | 1 | - |
| - | 1 | - | - | - | - | - | - | - | ||
| - | - | 1 | - | - | - | - | - | - |
将6a1按照4+2的方式分解,有4种可能,占比为,
| 4a7 | 2a3 | 3 |
| 4a1 | 2a1 | 3 |
| 4a2 | 2a2 | 6 |
| 4a4 | 2a2 | 3 |
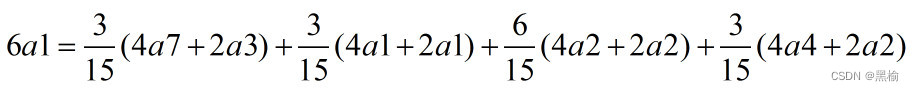
所以如果已知两个点按照2a2的方式飞出,
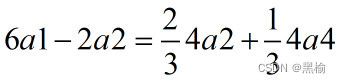
剩余的4个点,有2/3的可能按照4a2的方式运动,有1/3的可能按照4a4的方式运动。
假如一次飞出3个点
| 3a5 | 3a6 | |||||||||
| 1 | 1 | 1 | 1 | - | - | 1 | 1 | 1 | ||
| 1 | - | - | = | - | 1 | - | + | - | - | - |
| - | 1 | - | - | - | 1 | - | - | - | ||
| - | - | 1 | - | - | - | - | - | - | ||
| 3a3 | 3a1 | |||||||||
| 1 | 1 | 1 | - | - | 1 | 1 | 1 | - | ||
| 1 | - | - | = | - | - | 1 | + | - | 1 | - |
| - | 1 | - | 1 | - | - | - | - | - | ||
| - | - | 1 | - | - | - | - | - | - | ||
| 3a5 | 3a4 | |||||||||
| 1 | 1 | 1 | 1 | - | - | 1 | 1 | - | ||
| 1 | - | - | = | - | 1 | - | + | - | - | 1 |
| - | 1 | - | - | - | 1 | - | - | - | ||
| - | - | 1 | - | - | - | - | - | - |
6a1按照3+3的方式分解有3种可能,占比为
| 3a5 | 3a6 | 1 |
| 3a3 | 3a1 | 6 |
| 3a5 | 3a4 | 3 |
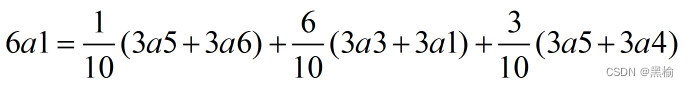
所以如果已知3个点按照3a5的方式飞出,
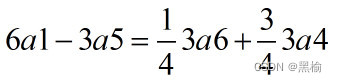
剩余的3个点有1/4的可能按照3a6的方式运动,有3/4的可能按照3a4的方式运动。是一个复合态。
所以如果有一个函数φ1把直线上的n个点,映射为平面上的一种运动方式比如结构x,而另一个函数φ2把平面上的m个点映射为平面上的另一种运动方式结构y,现在φ1和φ2之间作用的结果就取决于两个结构x,y,只要x和y是已知的φ1和φ2的作用结果就是可计算的,而不必知道φ1和φ2的解析式。
