人工智能基础_机器学习040_Sigmoid函数详解_单位阶跃函数与对数几率函数_伯努利分布---人工智能工作笔记0080

然后我们再来详细说一下Sigmoid函数,上面的函数的公式

我们要知道这里的,Sigmoid函数的意义,这逻辑斯蒂回归的意义就是,在多元线性回归的基础上,把
多元线性回归的结果,缩放到0到1之间对吧,根据中间的0.5为分类,小于0.5的一类,大于的一类,
这里的h theta(x) 就是概率函数

然后我们这里要知道函数中theta T x这个部分,就是我们之前的线性回归方程,然后
我们把这个线性回归方程,用e-thetaTx来代替,做为一个整体来看待,然后 用1/1+的形式,这样
就把结果,缩小到0到1之间
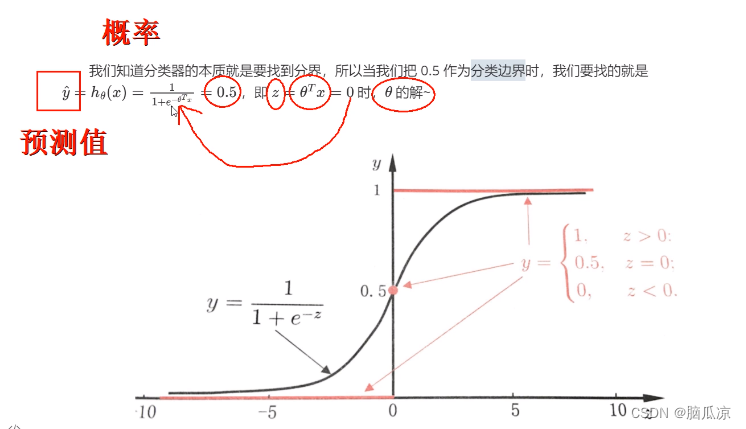
然后我们看这个函数,让它为0.5的时候,那么
骑行就是让thetaTx为-的时候,对吧
如果thetaTx是0,那么预测值,yhat = 1/1+1 = 1/2 = 0.5 对吧带入就可以看出来
