当前位置： 首页 > news >正文

C++ RBTree 理论

news 2025/8/2 21:06:56

目录

这个性质可以总结为

红黑树的最短最长路径

红黑树的路径范围

code

结构

搞颜色

类

插入

插入逻辑

新插入节点

思考：2. 检测新节点插入后，红黑树的性质是否造到破坏？

解决方法

变色

旋转+变色

第三种情况，如果根节点上面还有节点

这个性质可以总结为

1.每个节点不是红色就是黑色

2.根节点是黑色的

3.不能有两个连续的红色节点  ，即可以出现 红黑  黑黑 不能出现红红

4.每条路径上的黑色机节点数量不一样

至于性质5:每个叶子结点都是黑色的，这里的叶子节点并不是真的叶子节点，而是NIL节点，即空节点。如图（a）：

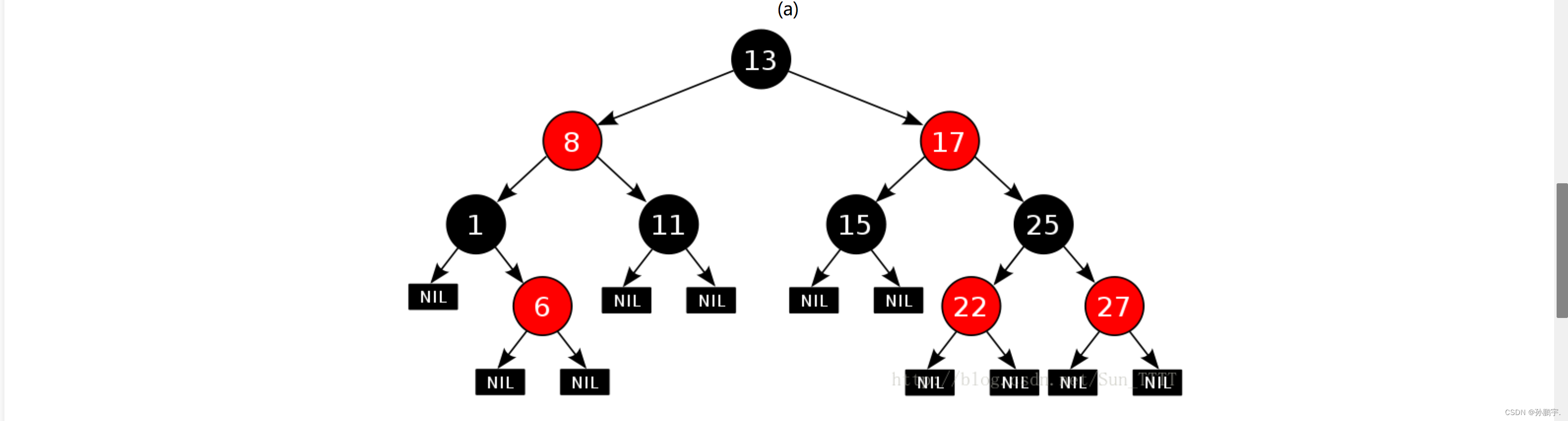
NIL节点有什么作用？如图（a-2），有多少条路径: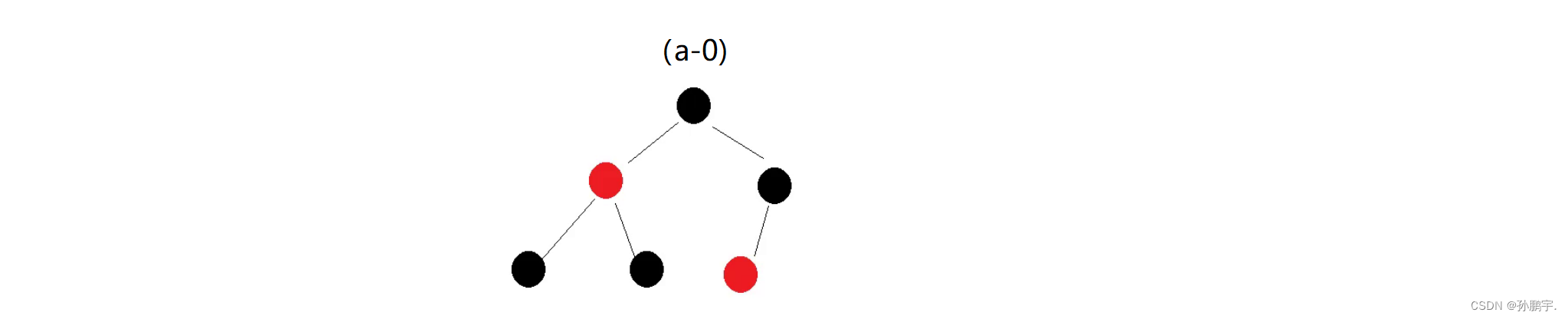

正确答案是有7条。路径路径的判断规则是：从根节点到NULL。

如果我们把NIL节点标记出来就好找路径了：

再比如，图(a-3)是否是红黑树：

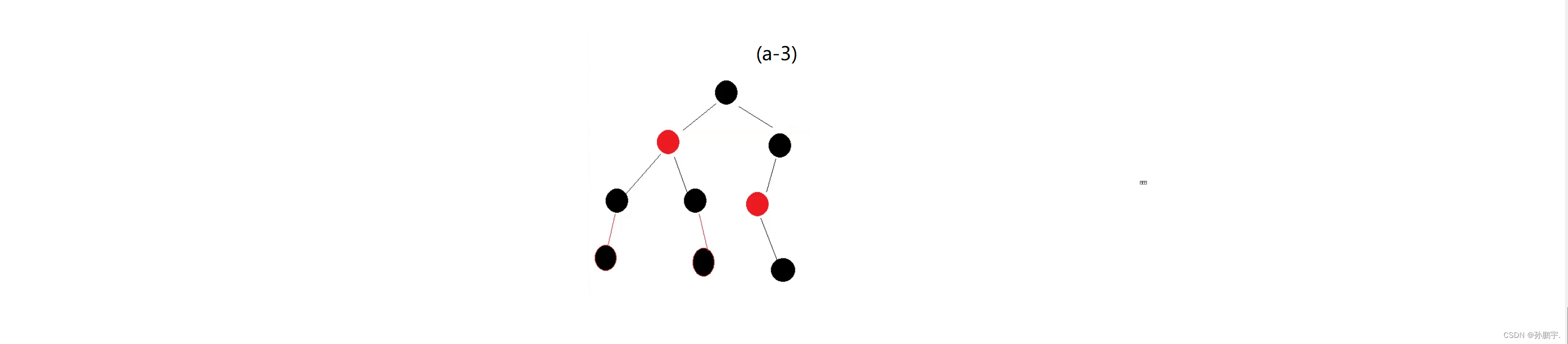
大致一看好像是，但是把NIL节点标出来之后:

 路径(b)只有两个黑色节点，不满足红黑树的性质，不是红黑树。

红黑树的最短最长路径

那么红黑树的最短路径是什么样子的，应该是全黑的最短：

 那最长的路径呢，应该是一黑一红间隔排列的最长：

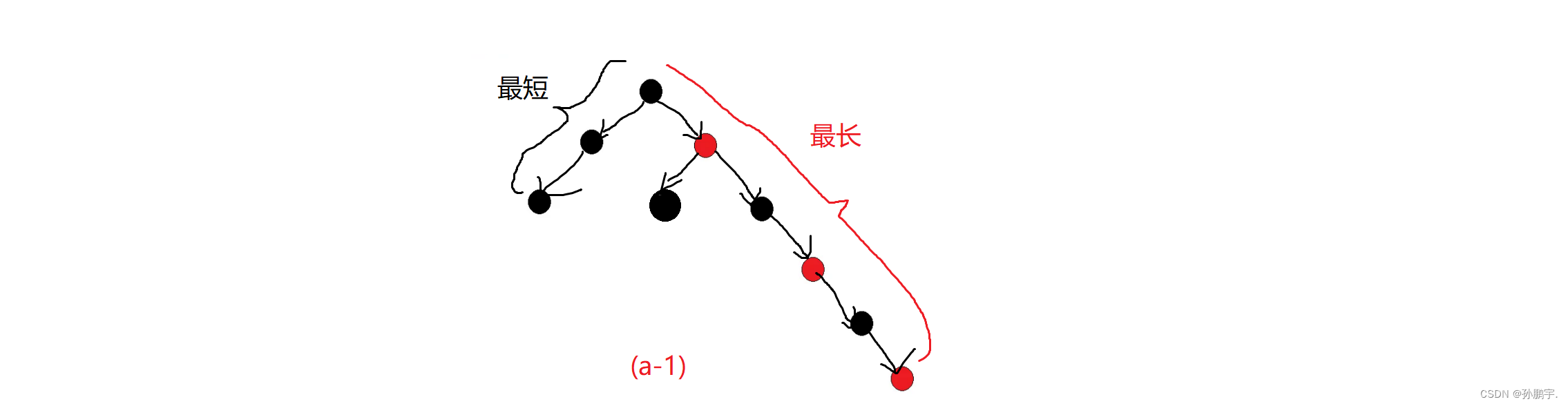根据图(a-1）我们可以看出，最长的路径是最短的路径的2倍。

ps

一个红黑树不一定有最长路径，也不一定有最短路径。

如图（a-2），有最短路径，没有最长路径:

红黑树的路径范围

而知道了最短路径，最长路径，剩下的路径都在最短路径，最长路径范围内，可以写为

                             [n,2*n]

code

结构

template<class K,class V>struct	RBTreeNode
{RBTreeNode<K,V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* parent;pair<K, V>;Color _col;//初始话列表RBTreeNode(const pair<K, V>kv):_left(nullptr),_right(nullptr), _parent(nullptr), pair<K, V>,_col(RED){}
};

搞颜色

enum Color
{RED,BALACK
};

类

template<class  K,class V>class RBTree{typedef RBTreenode<k,v> Node;public:private:Node* _root = nullptr;};

插入

插入逻辑

如果节点为空，就给黑色。如果节点不为空，就插入值。

这个值如果比根节点小，就往左边插入，否则就往右边插入。

bool Insert(const pair<K, v>& kv){if (_root == nullptr){_root = new(kv);_root->_col = BALACK;return true;}//初始化父亲节点和根节点Node* parent = nullptr;Node* cur = _root;while (cur){//key值大，往右走if (cur->kv.first < kv.first){cur = cur->right;}//key值小，往左走else if (cur->kv.first > kv.first){cur = -cur->left;}//否则key值和当前节点相等，不插入else{return false;}}//找到了返回true1return true;	 }

新插入节点

思考：2. 检测新节点插入后，红黑树的性质是否造到破坏？

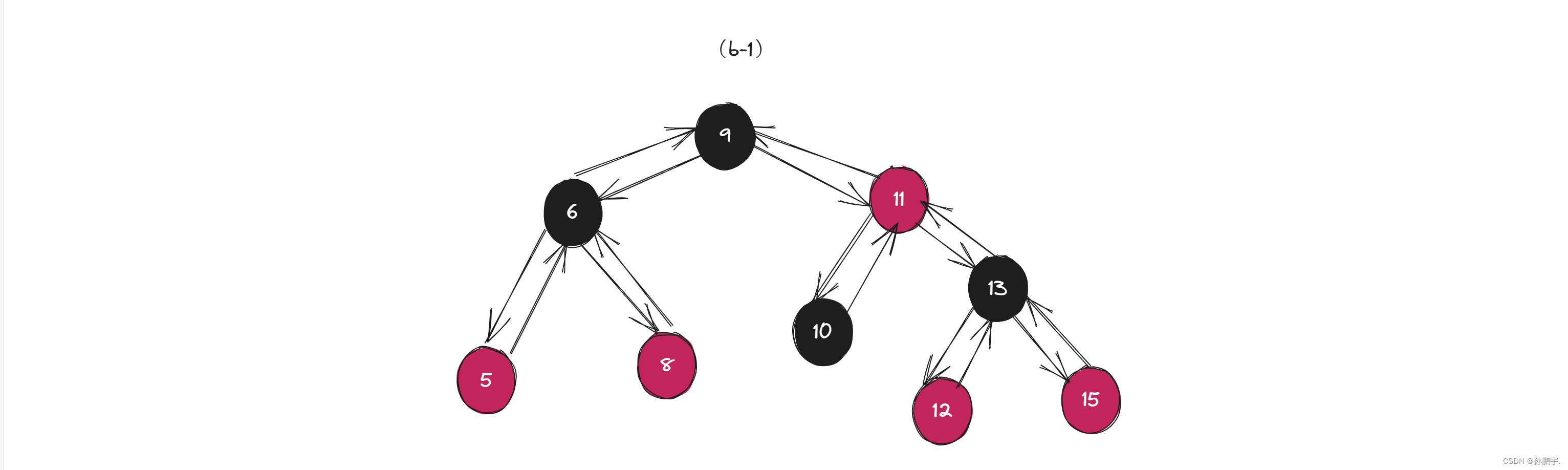
如图（b-1），现在要插入一个节点，那么是插入一个黑色节点还是红色节点呢？

如果插入黑色节点，那么该路径就会多一个黑色节点，根据红黑树特性，其他路径都要补一棵黑色节点，

如果插入红色节点，则只会影响父节点

（即

1.如果父节点也会红节点。两个红节点不能紧挨，需调整

2.如果父亲节点是黑色，则不需调整，直接插入。）。

我们看一下怎么调整，如图（b-2），新插入了一个红色节点7：

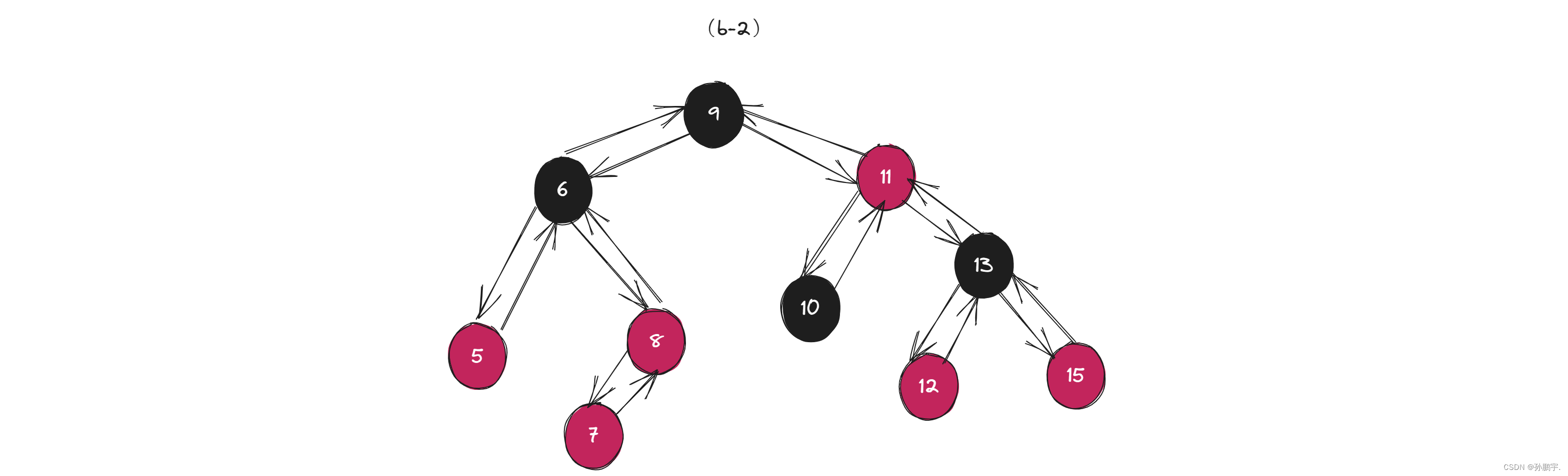
解决方法

能变色先变色，变色完之后还不行再旋转

变色

如图(b-3)，先把父节点8变黑：

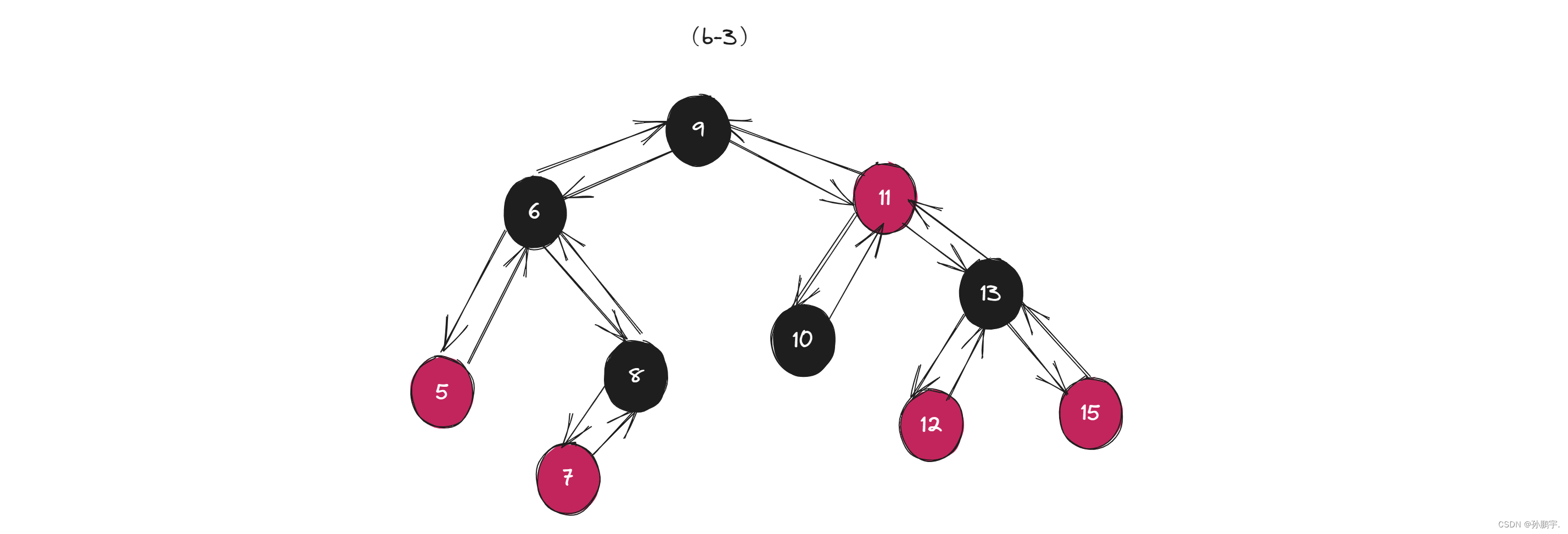
这个时候该路径就多了一个黑色节点，再变图(b-4）把6节点变红：

这个时候该路径又少了个黑色节点，再变图（b-5） 把5节点变黑：

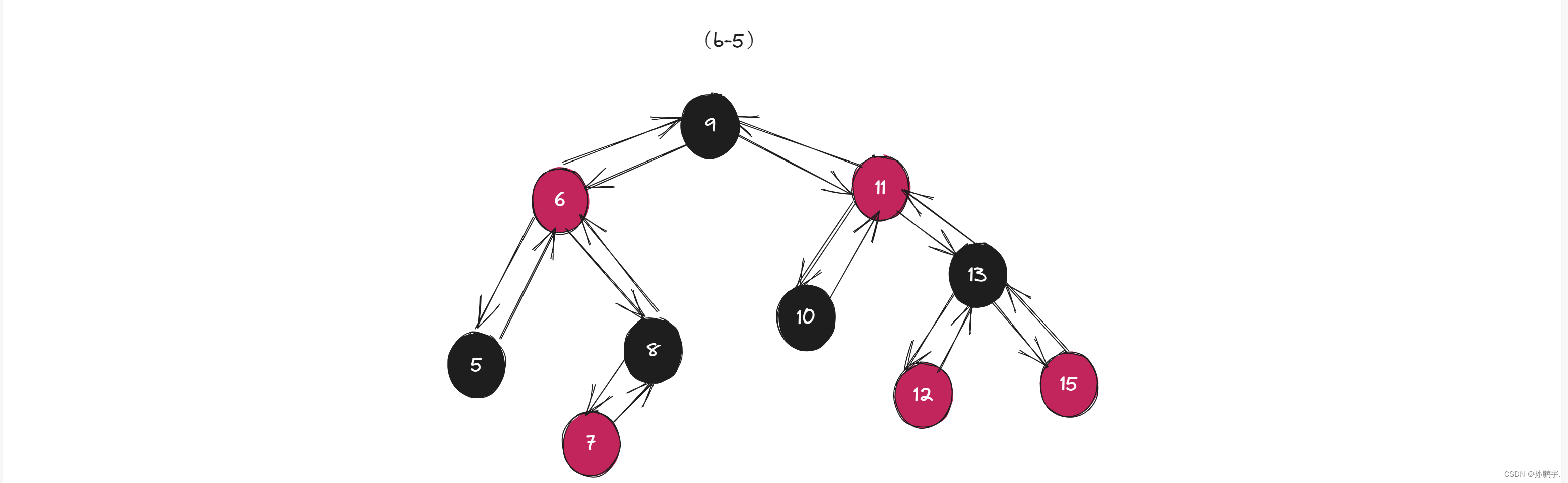
旋转+变色

第二种情况，例如图(b-6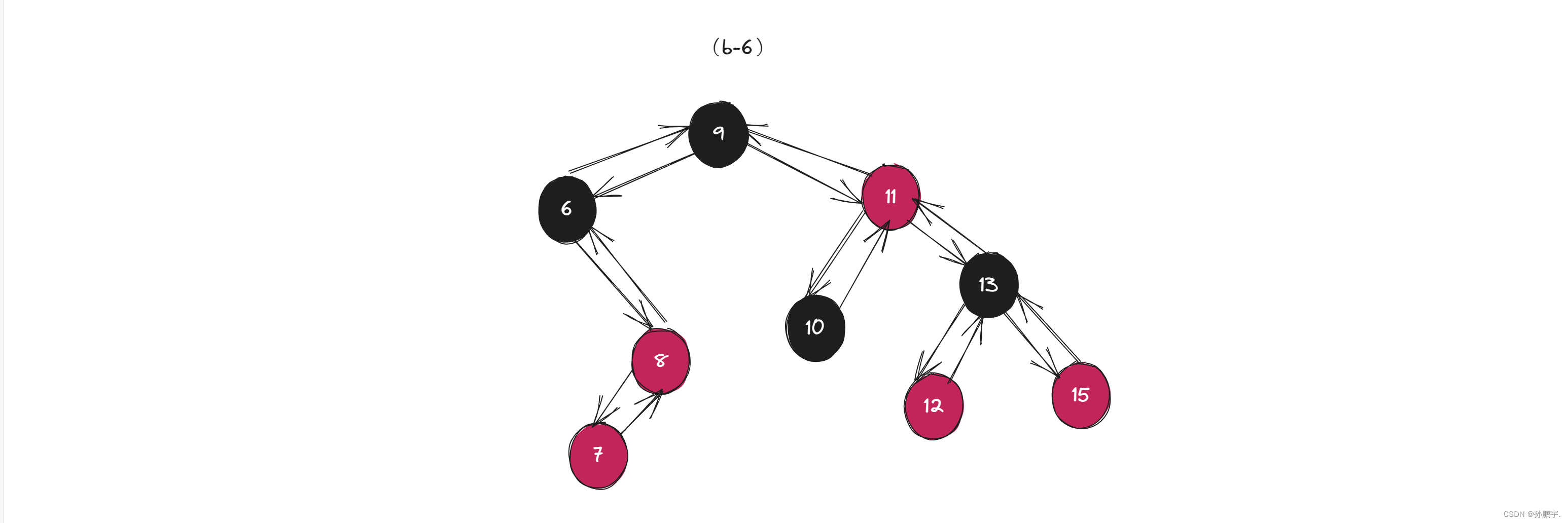）：如果还是把父节点变为黑色，把6节点变为红色，那么其他路径就会多一个黑色节点。

而该路径又没有其他节点可以再变黑色来平衡这种状态，所以靠变色解决不了这个问题。

这个时候就要旋转了。

先右旋为图（c-1）：

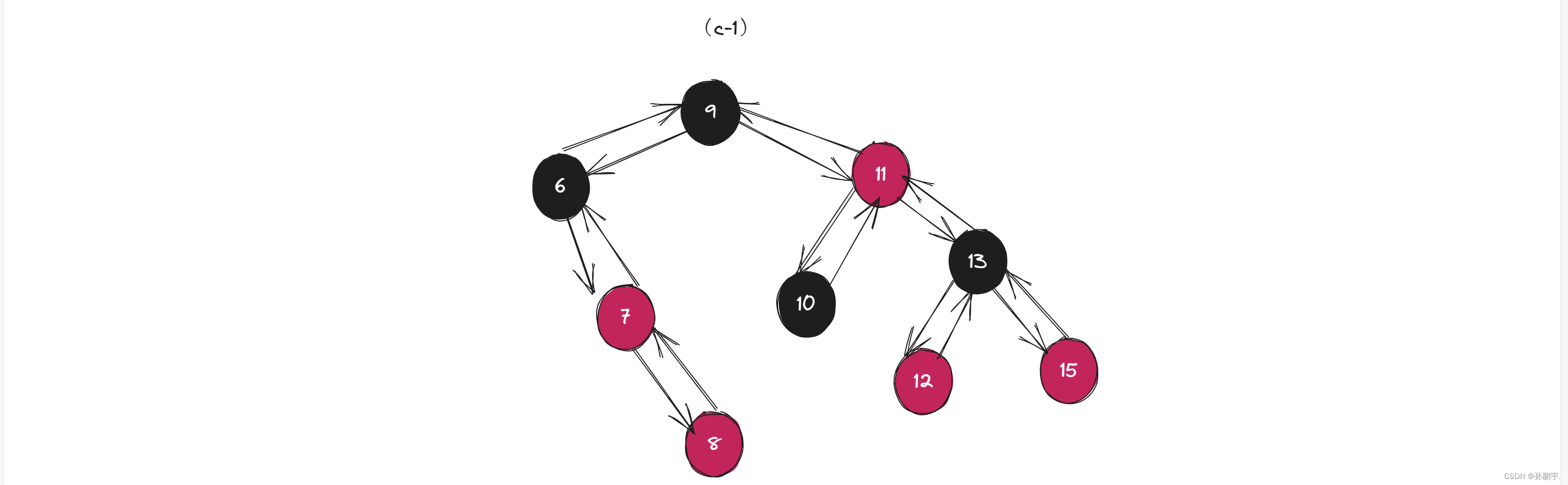再左旋为图（c-2）:

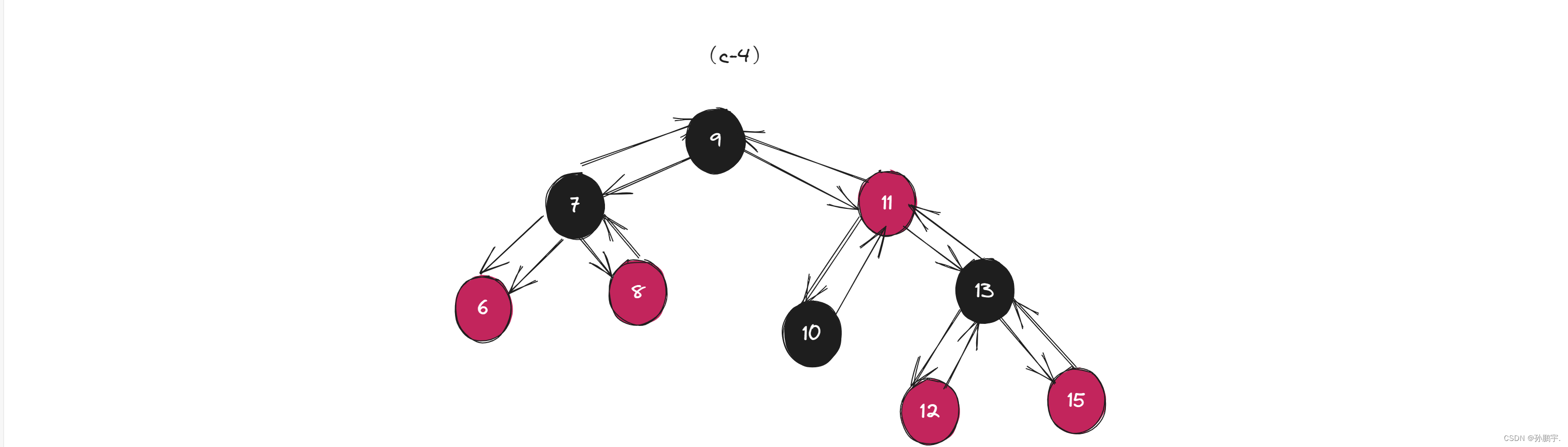
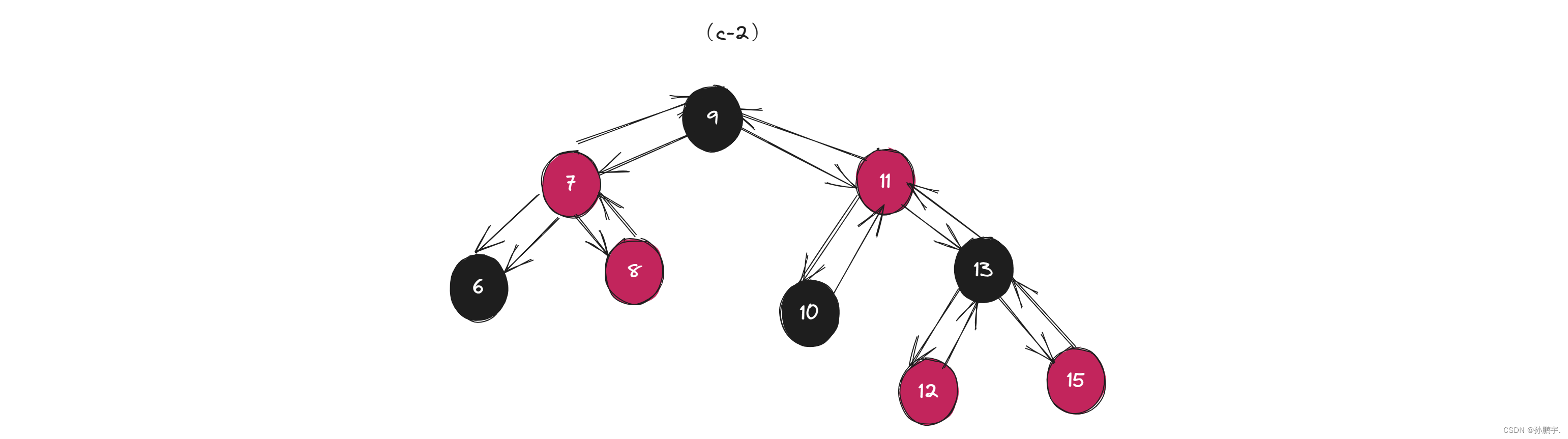然后再变色为图(c-4）：

情况一: cur为红，p为红，g为黑，u存在且为红

解决：叔叔存在，  变色

如图(d-0)，新插入了一个节点cur:

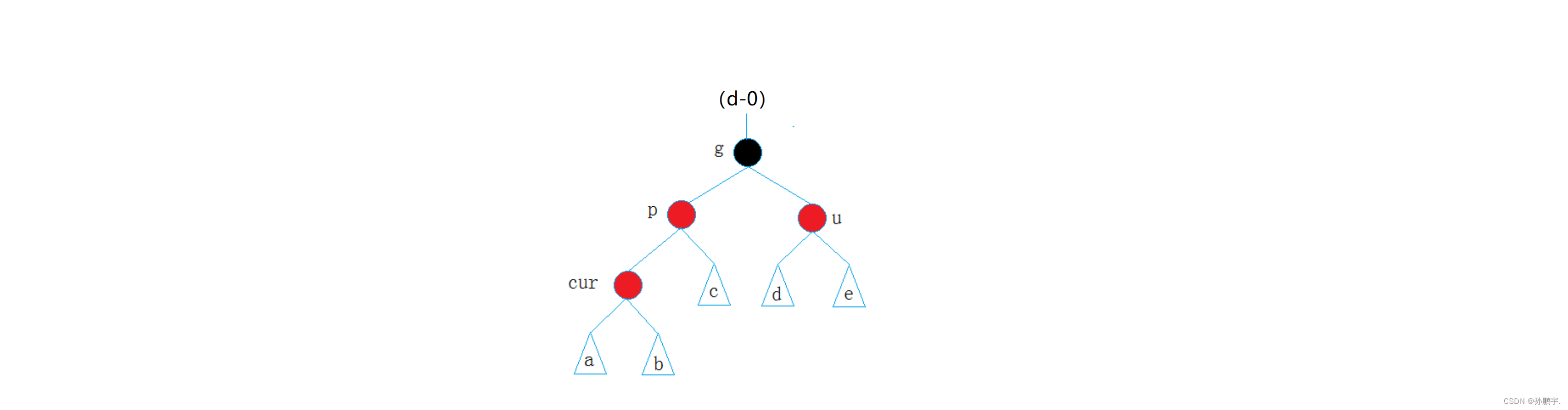
cur为红色节点，那就需要调整。

把p节点变为黑色节点，那么u节点也要变为黑色节点，那么此时就要把g节点变为红色节点。也就是图(d-1):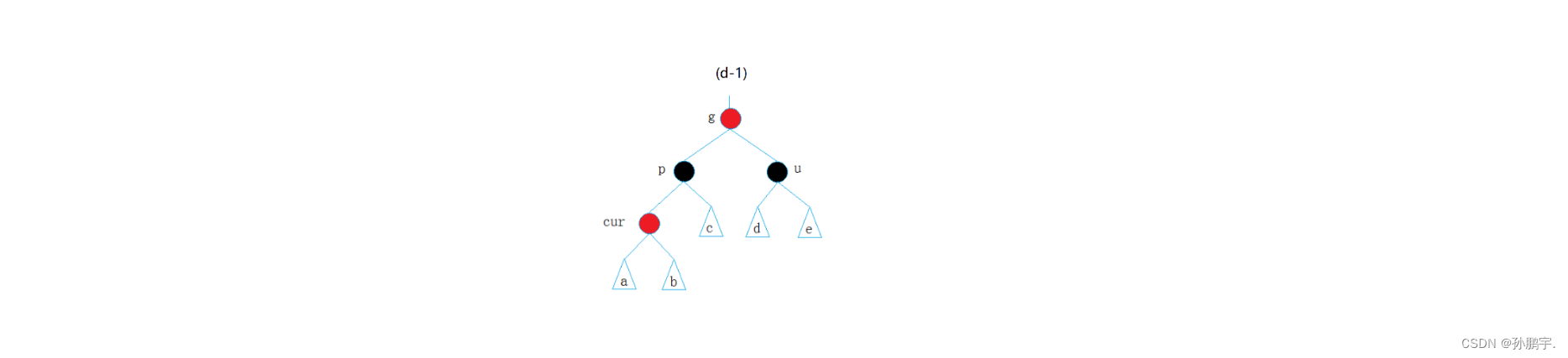

为什么要把g节点变为红色节点呢？

假设g节点不变为红色也就是图（d-3）:

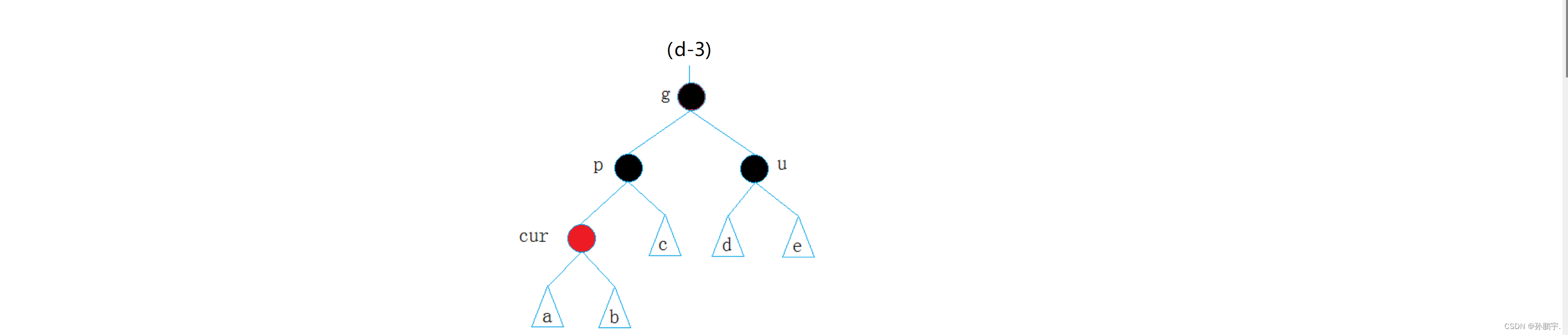
由图(d-1）变为图(d-3）我们发现每条路径凭空多了1个黑色节点。

g节点上面还有节点，那么多了个黑色节点，就会影响上面的路径，所以需要把g节点变红来平衡一下。

如图(d-1）：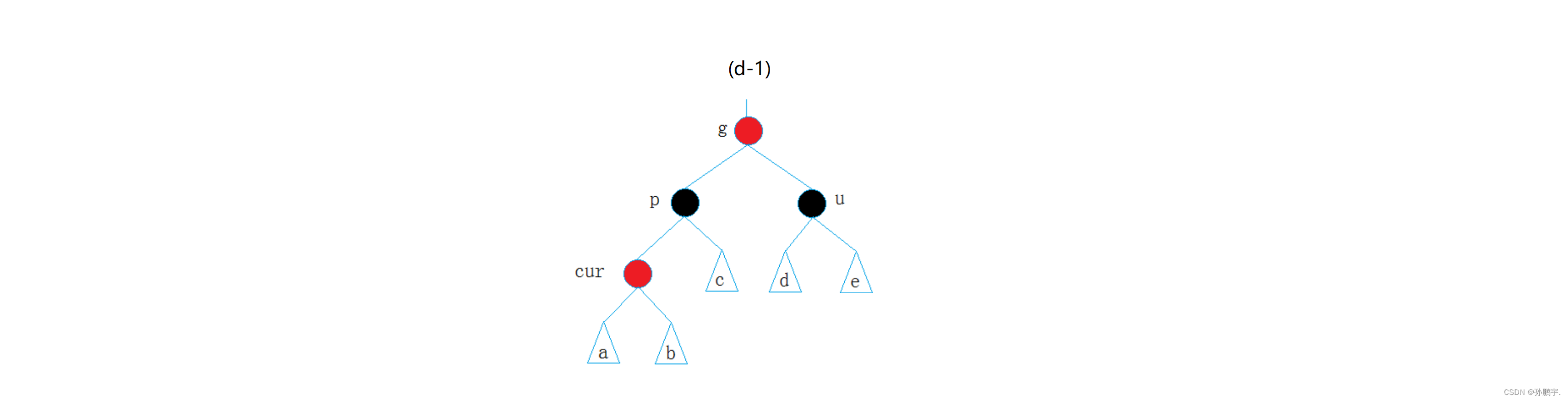

这个时候万一g节点的父节点是红色节点，如图(d-4）：
两个红色节点不能连续，还要调整，如果g节点的父亲节点为黑色，如图(d-5），那就不需要再调整:

 新增节点给红色：

cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){paret->_right = cur;cur->_parent = parent;}else if (_parent->_kv.first > kv.first){parent->_left = cur;cur->_parent = parent;}

父亲节点是红色就调整，是黑色就不用调整:

          while (parent->_col = RED){}

父亲节点可能在左边(e-1)，也可能在右边(e-2)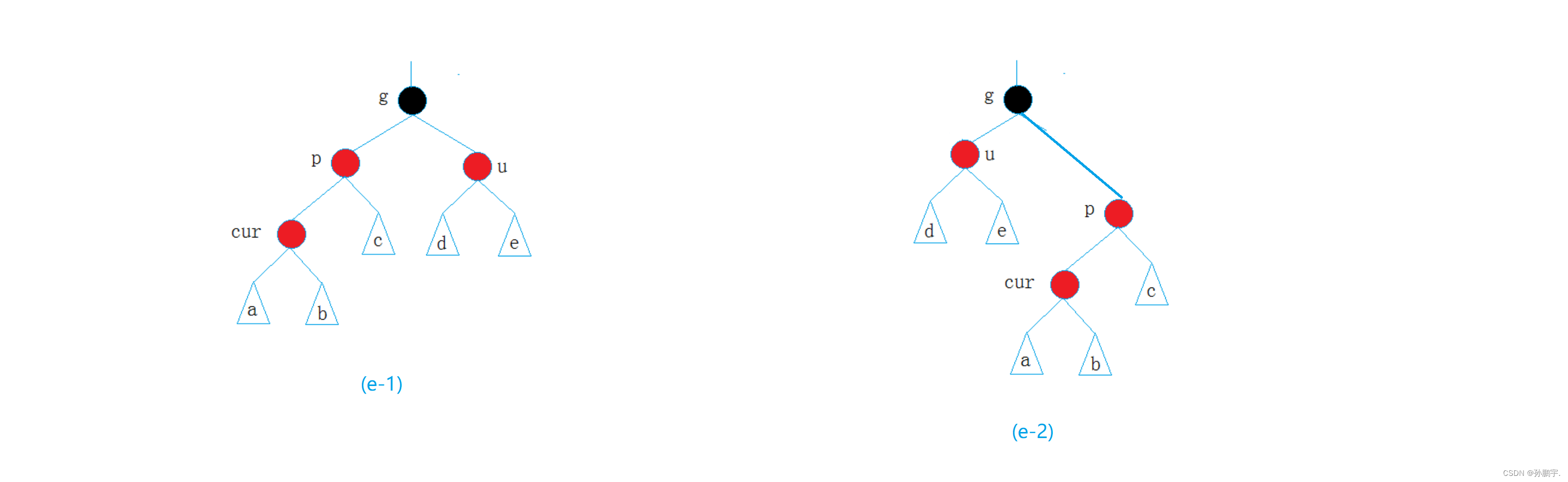：但是不论父亲节点在左在右，父亲节点的父亲父亲节点肯定是granparent节点。

先说图(e-1）的情况（即父亲节点在左）：

按照之前的推演，应该先把父亲节点和叔叔节点变为黑色，然后为了防止影响了上面的节点，还要把grandparent节点变为红色：

while (parent&& parent->_col = RED)  //当父亲为红色时{Node* grandparent = parent->_parent;//祖父节点是父亲节点的父亲节点if (parent = grandparent->_left)//第一种情况，叔叔节点在右时{Node* uncle = grandparent->_right;//叔叔节点在祖父节点的右边if (unlce && unluce->_col == RED){uncle->_col = parent->_col = BLACK;//叔叔节点的颜色要变成黑色grandparent->_col = RED;//祖父节为了平衡，要把父亲节的颜色变为红色

即变为图(d-1):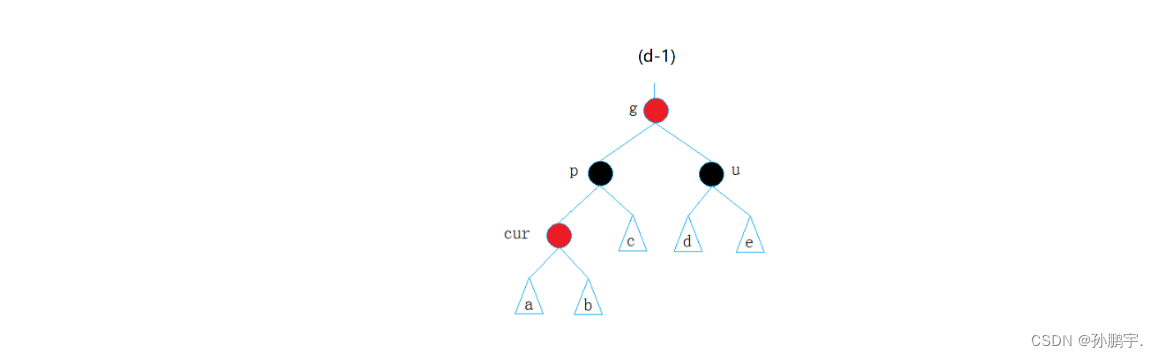

此时又有两种情况  （d-4）,(d-5)：

 （d-4）(d-5）的情况会在后续处理。

继续向上处理

这个时候把祖父节点当做当前节点，让祖父节点去找它的父亲

		}while (parent&& parent->_col = RED)  //当父亲为红色时{Node* grandparent = parent->_parent;//祖父节点是父亲节点的父亲节点if (parent = grandparent->_left)//第一种情况，叔叔节点在右时{Node* uncle = grandparent->_right;//叔叔节点在祖父节点的右边if (unlce && unluce->_col == RED){uncle->_col = parent->_col = BLACK;//叔叔节点的颜色要变成黑色grandparent->_col = RED;//祖父节为了平衡，要把父亲节的颜色变为红色//继续向上处理cur = grandparent;  //把祖父节点当做当前节点parent = cur->parent; //祖父节点去找它的父亲}}}

这个时候万一祖父节点向上不再有节点，祖父节点就是最终节点怎么办？

祖父节点若上面没有节点，那么祖父节点就是作为根节点，根节点不能为红，把根节点再变黑。(r如图（D-5）：

	 while (parent->_col = RED){Node* grandparent = parent->_parent;//祖父节点是父亲节点的父亲节点if (parent = grandparent->_left)//第一种情况，父亲节点是左子树，叔叔节点是右子树{Node* uncle = grandparent->_right;//叔叔节点在祖父节点的右边uncle->_col=parent->_col= BLACK;//叔叔节点的颜色要变成黑色grandparent->_col = RED;//祖父节为了平衡，要把父亲节的颜色变为红色}//把祖父当成当前节点，继续向上处理cur = grandparent;}//祖父节点向上不再有节点，祖父节点作为根节点，必须为黑色_root->_col = BACK;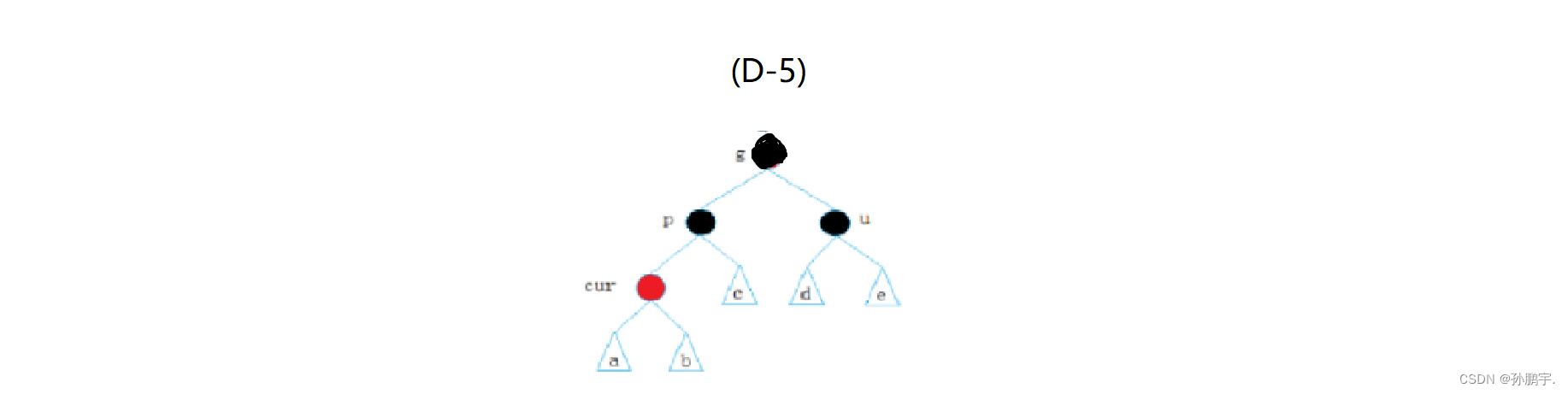

情况二: cur为红，p为红，g为黑，u不存在/u存在且为黑

解决：把祖父右旋走 ，让父亲做新根，根就要为黑色节点，再把父亲变黑：

图(0-0)到(0-1）为演变过程: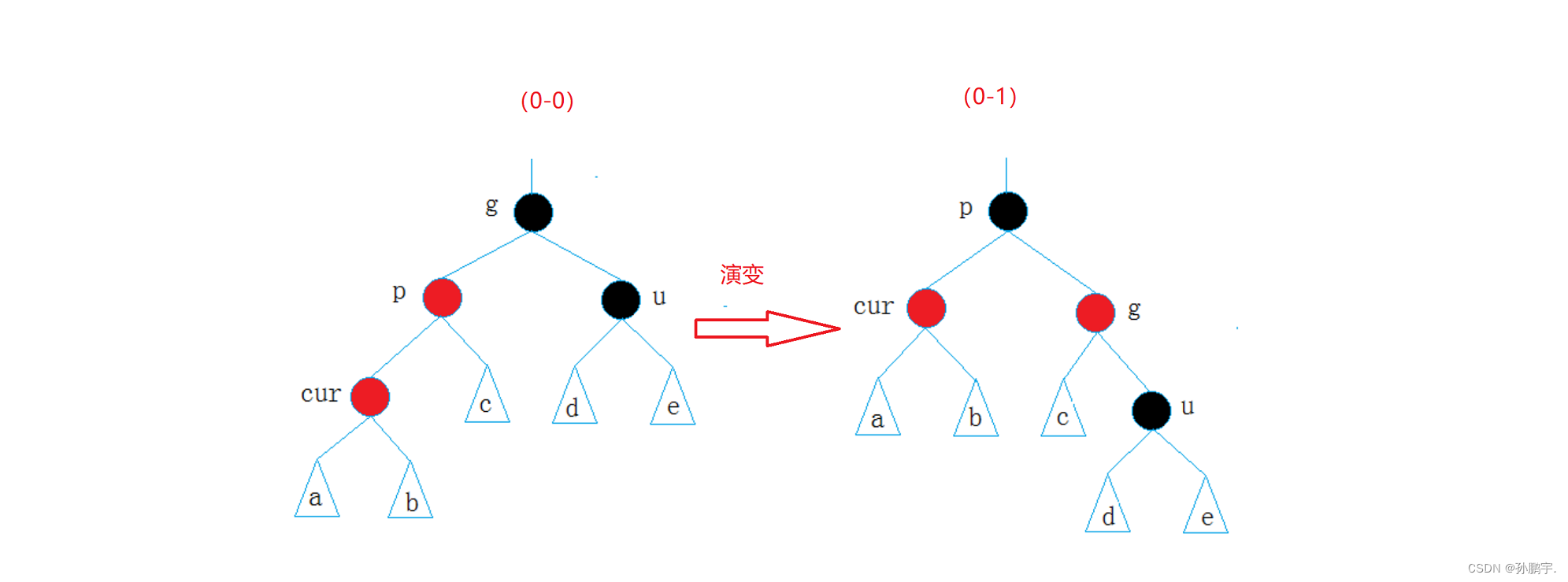

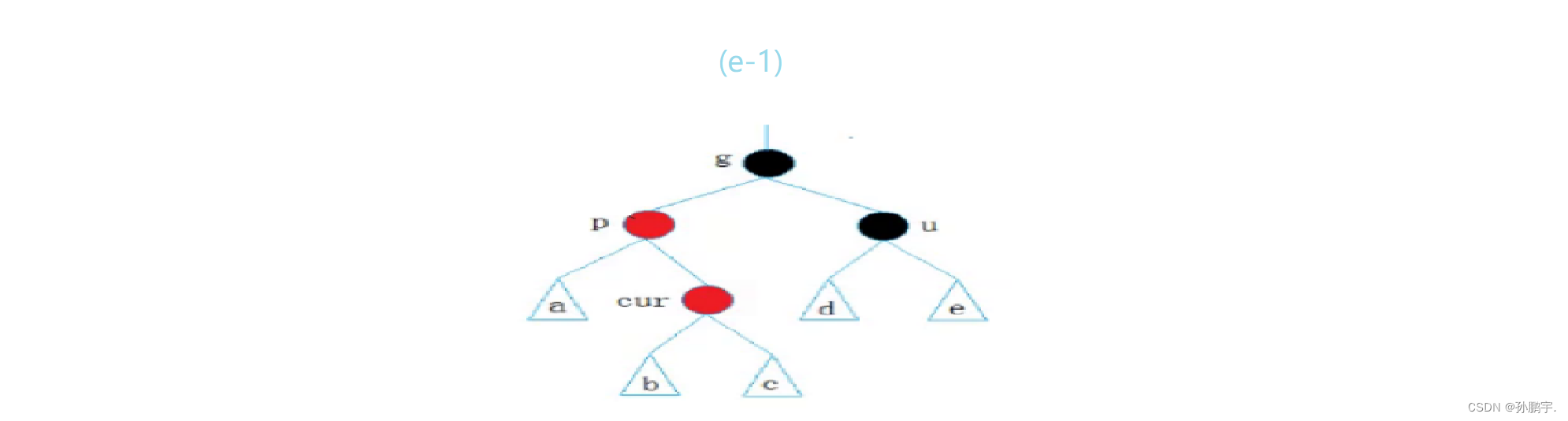
while (parent&& parent->_col = RED)  //当父亲为红色时{Node* grandparent = parent->_parent;//祖父节点是父亲节点的父亲节点if (parent = grandparent->_left)//第一种情况，叔叔节点在右时{Node* uncle = grandparent->_right;//叔叔节点在祖父节点的右边if (unlce && unluce->_col == RED){uncle->_col = parent->_col = BLACK;//叔叔节点的颜色要变成黑色grandparent->_col = RED;//祖父节为了平衡，要把父亲节的颜色变为红色//继续向上处理cur = grandparent;  //把祖父节点当做当前节点parent = cur->parent; //祖父节点去找它的父亲}else                           //第二种情况：叔叔节点在左边{if (cur == parent->left)  //当前节点在父亲节点的左边{							//单旋+变色  RotateR(granparent);    //旋转:把祖父右旋走，让父亲做新根parent->_col = BLACK;   //变色:做新根就要为黑色节点grandparent->_col = RED;  //祖父为了平衡变红}}}}//祖父节点向上不再有节点，祖父节点作为根节点，必须为黑色_root->_col = BLACK;

情况三：p为g的左孩子，cur为p的右孩子（如图e-1）

解决方案

（A）p为g的左孩子，cur为p的右孩子，则针对p做左单旋转；相反，
（B）p为g的右孩子，cur为p的左孩子，则针对p做右单旋转

图（e-1）符合(A）解决方案，以下是对图(e-1）用(A)方案进行推演的过程：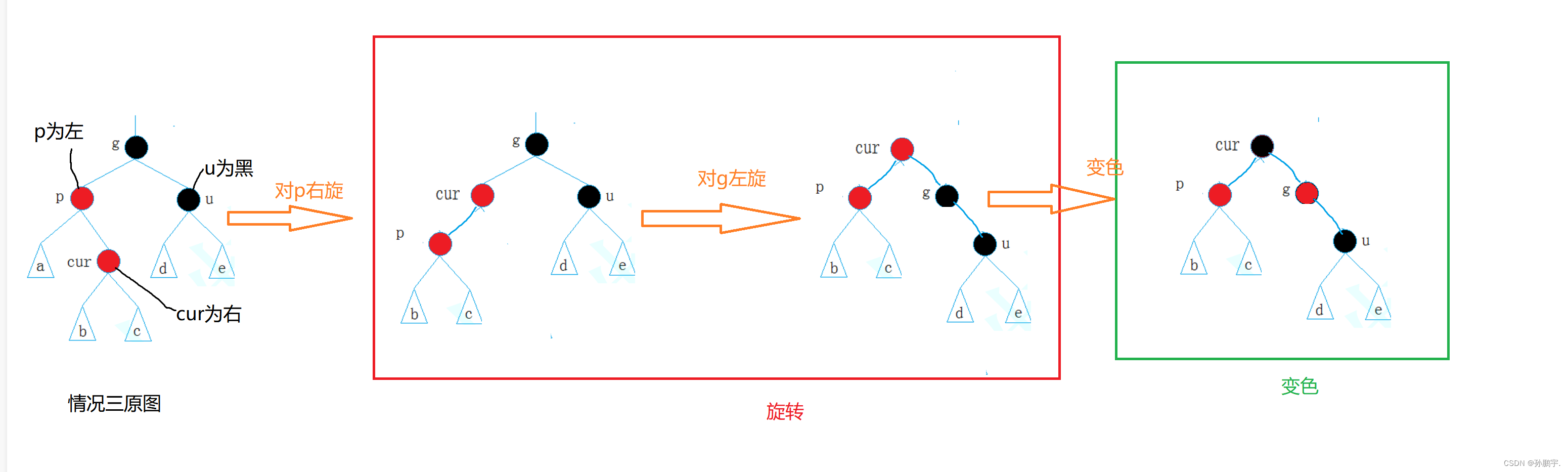

else 父亲在右边

如图（f-3）：

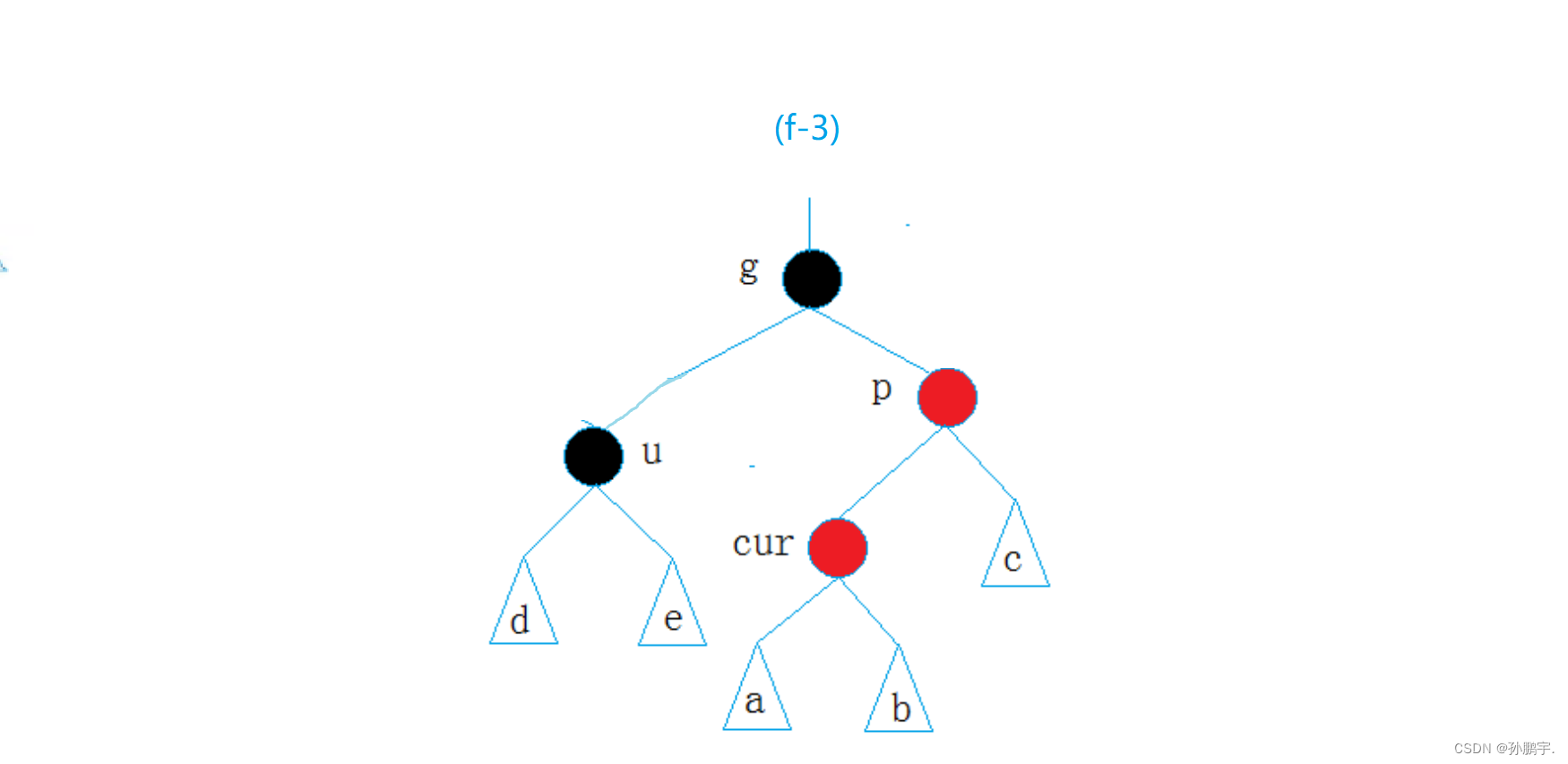
while (parent&& parent->_col == RED)  //当父亲为红色时{Node* grandparent = parent->_parent;//祖父节点是父亲节点的父亲节点if (parent = grandparent->_left)//第一种情况，叔叔节点在右时{Node* uncle = grandparent->_right;//叔叔节点在祖父节点的右边if (uncle && uncle->_col == RED){uncle->_col = parent->_col = BLACK;//叔叔节点的颜色要变成黑色grandparent->_col = RED;//祖父节为了平衡，要把父亲节的颜色变为红色//继续向上处理cur = grandparent;  //把祖父节点当做当前节点parent = cur->_parent; //祖父节点去找它的父亲}else                           //第二种情况：叔叔节点在左边{if (cur == parent->_left)  //当前节点在父亲节点的左边{							//单旋+变色  RotateR(grandparent);    //旋转:把祖父右旋走，让父亲做新根parent->_col = BLACK;   //变色:做新根就要为黑色节点grandparent->_col = RED;  //祖父为了平衡变红}else                  //当前节点在父亲节点右边{                     //双旋  RotateL(parent);   //父亲右旋RotateR(grandparent);  //祖父右旋cur->_col = BLACK;  //当前节点变黑grandparent->_col = RED;  //祖变红}break;}}else    //父亲在右边{Node* uncle = grandparent->_left;//叔叔节点在祖父节点的右边if (uncle = grandparent->_left)  //叔叔在左边//变色if (uncle && uncle->_col == parent->_col == RED)  //if叔叔存在且颜色为红色{uncle->_col = parent->_col = BLACK;  //叔叔父亲都变黑grandparent->_col = RED;   //祖父上面还有节点，要变红//继续向上处理cur = grandparent;}else //叔叔颜色为黑色{if (cur = parent->_right)  //叔叔在右边{RotateL(grandparent);  //左旋爷	parent->_col = BLACK;grandparent->_col = RED;  //祖变红}else   //叔叔在左边{//   g// u   p//   cRotateR(parent);  // 父亲右旋RotateL(grandparent);  //祖父旋走，让cur当根cur->_col = BLACK;   //根变黑色grandparent->_col = RED;  //祖父为了平衡变红色}}}}//祖父节点向上不再有节点，祖父节点作为根节点，必须为黑色_root->_col = BLACK;//找到了返回true1return true;
}

http://www.lryc.cn/news/229968.html

相关文章：

  • 制作这种在线宣传画册，可轻松收获客户！
  • 数据结构 | 图
  • [文件读取]shopxo 文件读取（CNVD-2021-15822）
  • zookeeper应用之分布式锁
  • 20. 机器学习——PCA 与 LDA
  • 深度学习准召
  • AtCoder ABC154
  • 可以非常明显地感受到，一场有关直播带货的暗流正在涌动
  • C++中的四种构造函数
  • 通过反射获取某个对象属性是否存在，并获取对象值
  • 【MySQL】存储过程与函数
  • 【数学】Pair of Topics—CF1324D
  • Qt文档阅读笔记-Fetch More Example解析
  • QtC++与QTableView详解
  • HG/T 6002-2022 氟树脂粉末涂料检测
  • 【java】idea可以连接但看不到database相关的files
  • 信驰达科技加入车联网联盟(CCC)，推进数字钥匙发展与应用
  • p9 Eureka-搭建eureka服务
  • 阶段七-Day01-SpringMVC
  • Python---集合中的交集 、并集 | 与差集 - 特性
  • C++调用lua脚本，包括全局函数绑定、类绑定，十分钟快速掌握
  • 快乐数[简单]
  • Spring源码阅读-ClassPathXmlApplicationContext
  • 考研分享第2期 | 中央财经大学管理科学跨考北大软微金融科技406分经验分享
  • Linux安装java jdk配置环境 方便查询
  • 惊群效应之Nginx处理
  • SpringBoot整合Ldap--超详细方法讲解
  • 【工程实践】Docker使用记录
  • FreeSwitch安装视频
  • SpringBoot3+Vue3+Mysql+Element Plus完成数据库存储blob类型图片，前端渲染后端传来的base64类型图片