当前位置：首页 > news >正文

Sequence（矩阵连乘+数论）

news 2025/8/11 22:36:33

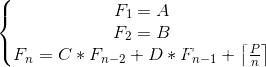
求Fn mod 1e9+7

Input

第一行是一个t代表有t组数据
接下来有t行每行有6个整数A,B,C,D,P,n
1<=t<=10
0<=A,B,C,D<=1e9
1<=p,n<=1e9

Output

输出一个答案Fn对1e9+7取余

Sample Input

2 
1 1 1 1 1 5
1 1 1 1 10 4

Sample Output

9
10

思路：

p/n上取整，一直会随着n的变化而变化，所以我们可以分一段一段的计算；

p/n上取整=(p+n-1)/n=(p-1)/n+1;

有个数学小知识：求∑(1,n)⌊k/i⌋∗i-CSDN博客

当我们知道一段区间的下界i，我们可以利用k/(k/i),求出其上界;

当我们知道一段区间的下界时，可以计算出它的上界，快速幂连乘即可。

代码：

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<unordered_map>
#include<map>
using namespace std;
typedef long long LL;
typedef unsigned long long ull;
#define per(i,a,b) for(int i=a;i<=b;i++)
#define ber(i,a,b) for(int i=a;i>=b;i--)
const int N = 1e5;
const long long mod = 1e9+7;
const double eps = 1e-2;
typedef struct data
{
LL m[3][3];

}J;
J Q,E;
LL a, b, c, d, p, n;
J now, e,ans;
LL f[3],tmp[3];
void into()
{
   Q= { d,c,1,
       1,0,0,
       0,0,1 };
   E = { 1,0,0,
       0,1,0,
       0,0,1 };
}
J quickfu(J a, J b)
{
   J c;
   for (int i = 0; i <= 2; i++)
       for (int j = 0; j <= 2; j++)
       {
           c.m[i][j] = 0;
           for (int k = 0; k <= 2; k++)
               c.m[i][j] = (c.m[i][j] + a.m[i][k] * b.m[k][j] % mod) % mod;
           c.m[i][j] = (c.m[i][j] % mod + mod)%mod;
       }
   return c;
}
J quick(J a, LL b)
{
   J ans = e;
   while (b)
   {
       if (b & 1)
           ans = quickfu(ans , a);
       b >>= 1;
       a = quickfu(a, a);
   }
   return ans;
}
int main()
{
   int T;
   cin >> T;
   while (T--)
   {
       cin >> a >> b >> c >> d >> p >> n;
       into();
       now = Q;
       e = E;
       if (n == 1)
       {
           cout << a % mod << endl;
           continue;
       }
       if (n == 2)
       {
           cout << b % mod << endl;
           continue;
       }
       p -= 1;
       f[0] = b, f[1] = a;
       for (LL i = 3, j = 1; i <= n; i = j + 1)
       {
           f[2] = p / i + 1;
           LL x =p / i;
           if (x == 0)
               j = n;
           else
           j = min(n, p / x);
           ans = quick(Q, j - i+1);
           for (int l = 0; l <= 2; l++)
           {
               tmp[l] = 0;
               for (int w = 0; w <= 2; w++)
                   tmp[l] = (tmp[l] + ans.m[l][w] * f[w]) % mod;
           }
           for (int l = 0; l <= 2; l++)
               f[l] = tmp[l];
       }
       cout <<f[0]<< endl;
   }
   return 0;
}