【聚类】谱聚类解读、代码示例
【聚类】谱聚类详解、代码示例
文章目录
- 【聚类】谱聚类详解、代码示例
- 1. 介绍
- 2. 方法解读
- 2.1 先验知识
- 2.1.1 无向权重图
- 2.1.2 拉普拉斯矩阵
- 2.2 构建图(第一步)
- 2.2.1 ϵ\epsilonϵ 邻近法
- 2.2.2 k 近邻法
- 2.2.3 全连接法
- 2.3 切图(第二步)
- 2.3.1 最小化 cut (A1, A2, . . . Ak)\text{cut (A1, A2, . . . Ak)}cut (A1, A2, . . . Ak)
- 2.3.2 RatioCut 切图
- 2.3.3 Ncut切图
- 3. 谱聚类流程
- 3.1 输入与输出
- 3.2 一般流程
- 4. 代码演示
- 5. 总结
- 6. 参考
1. 介绍
谱聚类的基本原理:
- 把所有数据看成空间中的点,这些点之间可以用变连接起;
- 距离较远的两个点之间的边权重较低,而距离较近的两个点之间的边权重较高;
- 通过对所有数据点组成的图进行切图,让切图后的不同的子图间边权重和尽可能小(即距离远),而子图内的边权重和尽可能高(即距离近)。
难点:
- 如何构建图?
- 如何切分图?
2. 方法解读
2.1 先验知识
2.1.1 无向权重图

2.1.2 拉普拉斯矩阵

2.2 构建图(第一步)
2.2.1 ϵ\epsilonϵ 邻近法

2.2.2 k 近邻法

2.2.3 全连接法
比前两种方法,第三种方法所有的点之间的权重值都大于0,因此称之为全连接法。
- 可以选择不同的核函数来定义边权重,常用的有多项式核函数,高斯核函数和Sigmoid核函数。
- 最常用的是高斯核函数 RBF。

2.3 切图(第二步)

其中Aiˉ\bar {\text{A}_i}Aiˉ 为 A\text{A}A 的补集。
进而,如何切图使子图内的点权重高,子图之间的点权重低?
2.3.1 最小化 cut (A1, A2, . . . Ak)\text{cut (A1, A2, . . . Ak)}cut (A1, A2, . . . Ak)
一个自然的想法就是最小化 cut (A1, A2, . . . Ak)\text{cut (A1, A2, . . . Ak)}cut (A1, A2, . . . Ak),但是可以发现,这种极小化的切图存在问题,如下图:
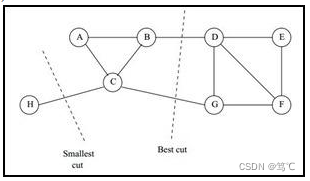
- 为了避免最小切图导致的切图效果不佳,我们需要对每个子图的规模做出限定;
- 一般来说,有两种切图方式,第一种是 RatioCut,第二种是 Ncut。
2.3.2 RatioCut 切图
对于每个切图,不仅要考虑最小化 cut (A1, A2, . . . Ak)\text{cut (A1, A2, . . . Ak)}cut (A1, A2, . . . Ak),还要考虑最大化每个子图样本的个数,即最小化 RatioCut函数:
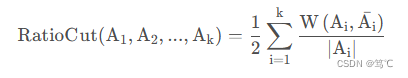

- 这里需要提一下,hih_ihi是正交基,但并不是单位正交基,因为hiThi=1∣Aj∣{h_i}^Th_i = \frac{1}{|A_j|}hiThi=∣Aj∣1,而不是1。但是不影响后面结论。
2.3.3 Ncut切图


3. 谱聚类流程
3.1 输入与输出
- 输入:样本集 D=(x1,x2,...,xn)D=(x_1, x_2,...,x_n)D=(x1,x2,...,xn),邻接矩阵的生成方式,降维后的维度k1,聚类方法,聚类后的簇个数k2;
- 输出: 簇划分C(c1,c2,...,ck2)C ( c_1, c_2,. . .,c_{k2})C(c1,c2,...,ck2)
3.2 一般流程
- 根据邻接矩阵生成方式构建邻接矩阵W,构建度矩阵D;
- 计算出拉普拉斯矩阵L;
- 构建标准化后的拉普拉斯矩阵D−12LD−12D^{-\frac {1}{2}}LD^{-\frac {1}{2}}D−21LD−21;
- 计算D−12LD−12D^{-\frac {1}{2}}LD^{-\frac {1}{2}}D−21LD−21最小的k1个特征值所各自对应的特征向量f;
- 将各自对应的特征向量f组成的矩阵按行标准化,最终组成n × k1 维矩阵F;
- 对F 中的每一行作为一个k1维样本,共n个样本,用输入的聚类方法进行聚类,聚类个数为k2;
- 得到簇划分C(c1,c2,...,ck2)C ( c_1, c_2,. . .,c_{k2})C(c1,c2,...,ck2)。
4. 代码演示
import numpy as np
import matplotlib.pyplot as plt
from sklearn import cluster, datasets
from sklearn.preprocessing import StandardScalernp.random.seed(0)# 数据构造
n_samples = 1500
noisy_circles = datasets.make_circles(n_samples=n_samples, factor=0.2, noise=0.05)
noisy_moons = datasets.make_moons(n_samples=n_samples, noise=0.05)
blobs = datasets.make_blobs(n_samples=n_samples, random_state=8)data_sets = [(noisy_circles, {"n_clusters": 3}),(noisy_moons, {"n_clusters": 2}), (blobs, {"n_clusters": 3})
]
colors = ["#377eb8", "#ff7f00", "#4daf4a"]
affinity_list = ['rbf', 'nearest_neighbors']plt.figure(figsize=(20, 15))for i_dataset, (dataset, algo_params) in enumerate(data_sets):params = algo_paramsX, y = datasetX = StandardScaler().fit_transform(X)for i_affinity, affinity_strategy in enumerate(affinity_list):spectral = cluster.SpectralClustering(n_clusters=params['n_clusters'],eigen_solver='arpack', affinity=affinity_strategy)spectral.fit(X)y_pred = spectral.labels_.astype(int)y_pred_colors = []for i in y_pred:y_pred_colors.append(colors[i])plt.subplot(3, 4, 4*i_dataset+i_affinity+1)plt.title(affinity_strategy)plt.scatter(X[:, 0], X[:, 1], color=y_pred_colors)# plt.show()
plt.savefig("a.jpg")
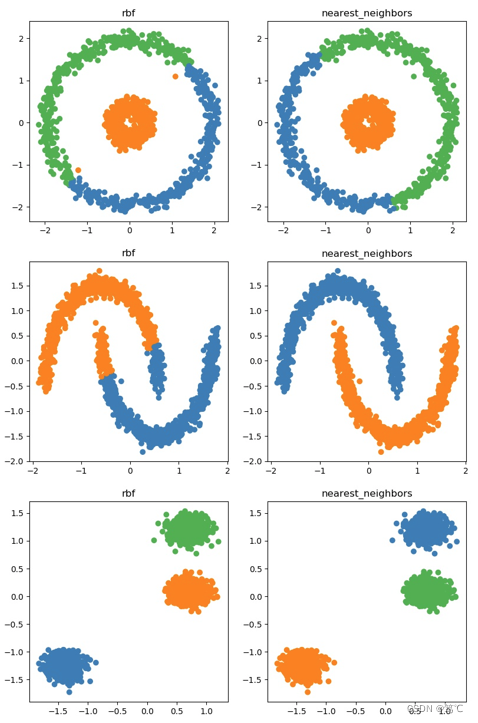
5. 总结
- 优点:
- 谱聚类只需要数据之间的邻接矩阵,因此对于处理稀疏数据的聚类很有效。这点传统聚类算法比如K-Means很难做到;
- 由于使用了降维,因此在处理高维数据聚类时的复杂度比传统聚类算法好。
- 缺点:
- 如果最终聚类的维度非常高,则由于降维的幅度不够,谱聚类的运行速度和最后的聚类效果均不好;
- 聚类效果依赖于邻接矩阵,不同的邻接矩阵得到的最终聚类效果可能很不同。
6. 参考
【1】https://blog.csdn.net/qq_42735631/article/details/121010760
