剑指 Offer 41. 数据流中的中位数
题目
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
例如,[2,3,4] 的中位数是 3, [2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
void addNum(int num) - 从数据流中添加一个整数到数据结构中。 double findMedian() -返回目前所有元素的中位数。

思路
优先队列 / 堆
给定一长度为
N的无序数组,其中位数的计算方法:首先对数组执行排序(使用O(NlogN)时间),然后返回中间元素即可(使用O(1)时间)
本题可以根据上述思想,将数据流保存在一个列表中,并在添加元素时保持数组有序,给定一长度为 N 的无序数组,其中位数的计算方法:首先对数组执行排序(使用 O(NlogN) 时间),然后返回中间元素即可(使用 O(1)时间)
借助 堆 进行优化时间复杂度
建立两个堆,一个小顶堆A,一个大顶堆B,各自保存列表的一半元素 ,其中:
- A保存较大的一半,长度为
N/2或者(N+1)/2 - B保存较小的一半,长度为
N/2或者(N+1)/2
最后,中位数可以仅根据A,B的堆顶元素计算得到:

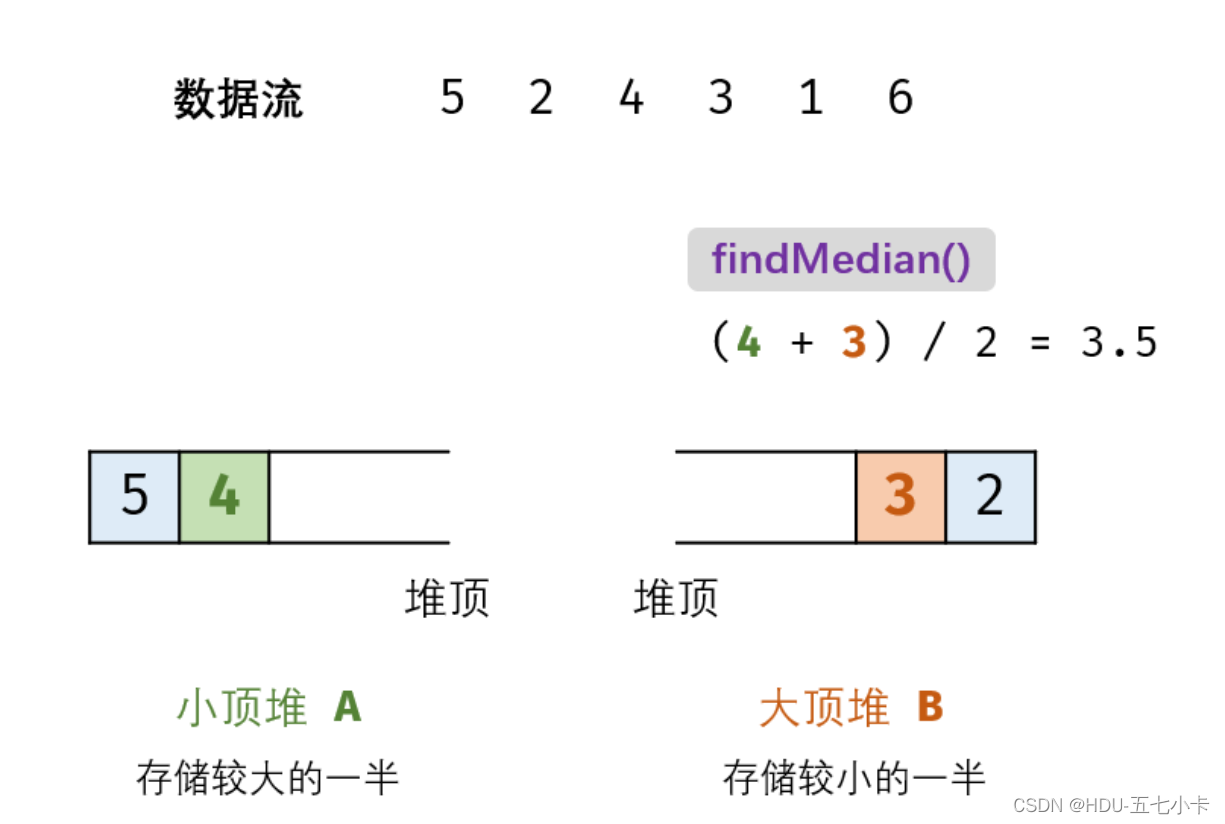
举个例子:数据流 [1,2,3,4,5,6,7,8]
如图所示,则[1,2,3,4]保存在大顶堆B,且堆顶元素为4(因为大顶堆堆顶元素最大),然后[5,6,7,8]保存在小顶堆A,且堆顶元素为5(因为小顶堆堆顶元素最小),这也是为什么大顶堆保存较小的一半,小顶堆保存较大的一半,为了就是可以通过A,B的堆顶元素求中位数
算法流程:
设元素总数为 N = m + n ,其中 m 和 n 分别为 A 和 B 中的元素个数
addNum(num)函数:添加元素,
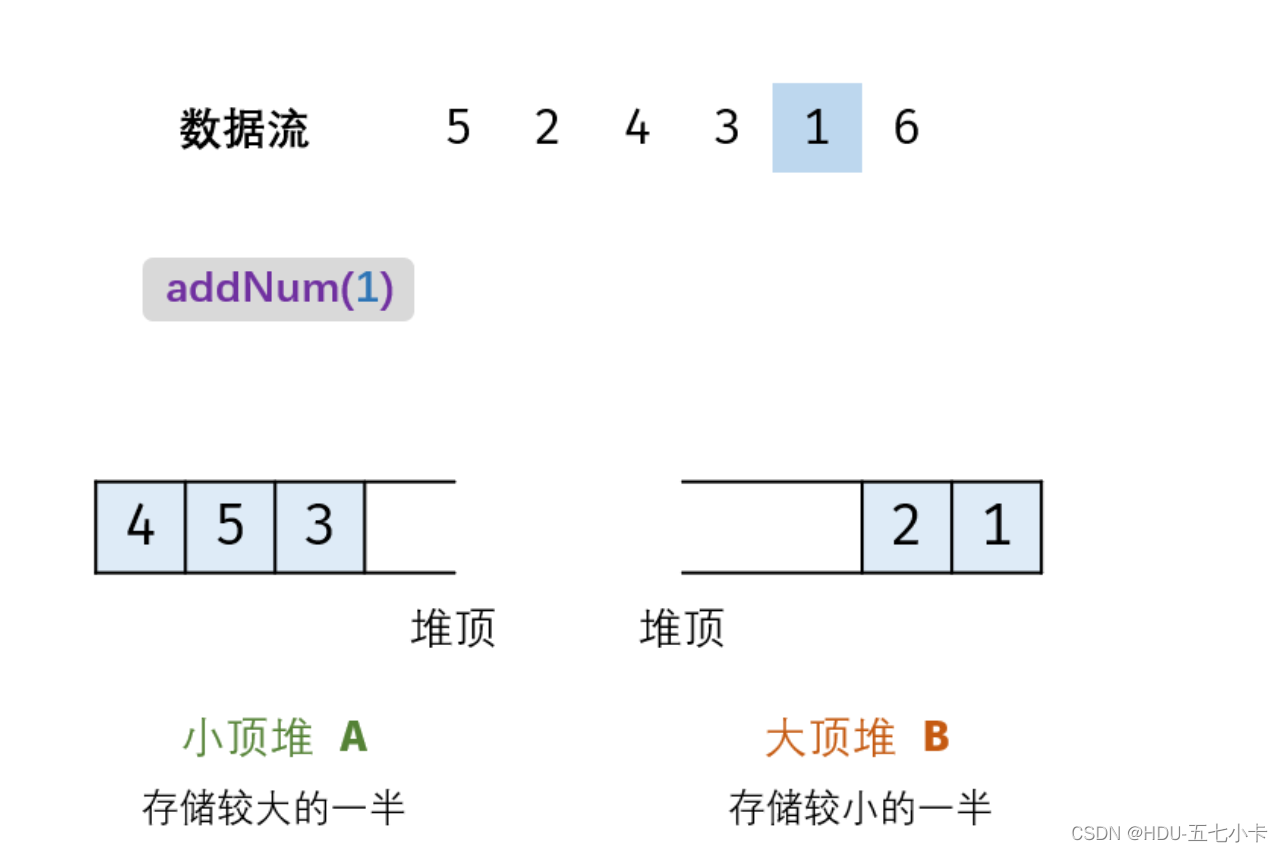
(1)当m=n(即N为 偶数):需向A添加一个元素,即A和B中元素个数相等时,优先往A中先加元素。实现方法:将新元素num插入至B,再将B堆顶元素插入至A(这是为了始终保证A中存较大的一半,B中存较小的一半,因为num可能属于较小的一半,即B中的元素,所以要先加入B,再将B堆顶元素插入A);
举个例子,A中加入1需要先加入B中,然后将B的堆顶元素3加入A
(2)当 m≠n(即 N 为 奇数):需向 B 添加一个元素,此时情况即为A比B多一个元素。实现方法:将新元素 num 插入至 A ,再将A 堆顶元素插入至 B (同理,为了始终保证A中存较大的一半,B中存较小的一半,要先加入A,再将A的堆顶元素插入B,因为num可能属于较大的一般分,即属于A的元素);
举个例子,B中加入6需要先加入A中,然后将A的堆顶元素3加入B
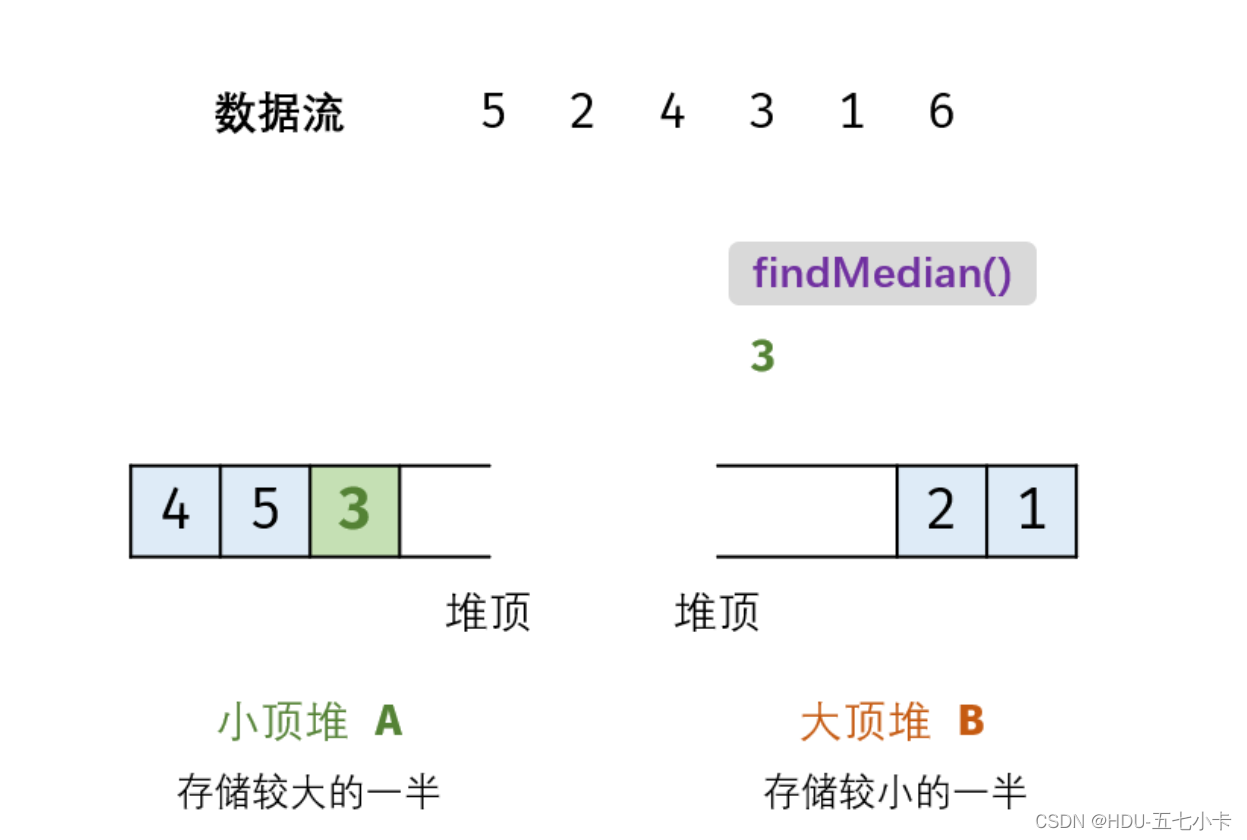

findMedian()函数:找中位数
(1)当m=n(N为 偶数):则中位数为 (A的堆顶元素 +B的堆顶元素 ) / 2
(2)当m≠n(N为 奇数):则中位数为A的堆顶元素。
复杂度分析:
- 时间复杂度:
(1)查找中位数O(1): 获取堆顶元素使用O(1)时间;
(2)添加数字O(logN): 堆的插入和弹出操作使用O(logN)时间 - 空间复杂度
O(N):其中N为数据流中的元素数量,小顶堆A和大顶堆B最多同时保存N个元素。
java代码如下:
class MedianFinder{Queue<Integer> A,B;public MedianFinder() {A = new PriorityQueue<>();//java默认小顶堆,保存较大的一半B = new PriorityQueue<>((x,y) -> (y - x));//使用降序定义大顶堆(因为大顶堆堆顶元素最大,所以是降序,但是用于升序排序,因为每次出堆顶元素是最大的),保存较小的一半}public void addNum(int num){if(A.size() != B.size()){//如果A,B元素个数不相等,则往B中添加元素//但是为了始终保证A中存较大的一半,B中存较小的一半A.add(num);//要先往A中加B.add(A.poll());//然后再将A的堆顶元素加入B} else {//如果A,B元素个数相等,则往A中添加元素//同理为了始终保证A中存较大的一半,B中存较小的一半B.add(num);A.add(B.poll());//要先往B中加//然后再将B的堆顶元素加入A}}public double findMedian(){return A.size() != B.size() ? A.peek() : (A.peek() + B.peek()) / 2.0;}
}
