ccc-台大林轩田机器学习基石-hw1
文章目录
- Question1-14
- Question15-PLA
- Question16-PLA平均迭代次数
- Question17-不同迭代系数的PLA
- Question18-Pocket_PLA
- Question19-PLA的错误率
- Question20-修改Pocket_PLA迭代次数
Question1-14

对于有明确公式和定义的不需要使用到ml

智能系统在与环境的连续互动中学习最优行为策略的机器学习问题,学习最优的序贯决策

无标签分类
从标注数据 学习预测模型

主动地提出一些标注请求,将一些经过筛选的数据提交给专家进行标注

- 解题关键是计算N+1到N+L上的偶数个数
- 0到N的偶数个数是⌊N⌋2\frac{ ⌊N⌋}{2}2⌊N⌋
- 问题转化成(0到N+L的偶数个数-0到N的偶数个数)

generate了D,但是N+1到N+L上L个点没有generate。每个点都有{被generate,没被generate}两种可能,所以是2L2^L2L

由“无免费午餐定理”可知,任何算法在没有噪声时对于未知样本期望相等

P(5orange&5else)=C105210P(5orange\&5else)=\frac{C_{10}^5}{2^{10}}P(5orange&5else)=210C105
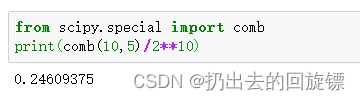
from scipy.special import comb
print(comb(10,5)/2**10)

P(9orange&1else)=C1090.99×0.1P(9orange\&1else)=\frac{C_{10}^9}{0.9^{9}\times0.1}P(9orange&1else)=0.99×0.1C109
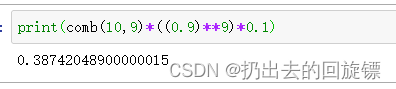
print(comb(10,9)*((0.9)**9)*0.1)

- 分v=0.1和0时讨论
P=C101(910)1(110)9+C100(110)10P=C_{10}^1{(\frac 9{10})^{1}{(\frac 1 {10})}^{9} }+C_{10}^0{{(\frac 1 {10})}^{10}}P=C101(109)1(101)9+C100(101)10


Hoeffding:P[∣μ−v∣>ϵ]≤2e−2ϵ2NP[v≤0.1]=P[0.9−v≥0.8]=P[μ−v≥0.8]≤P[∣μ−v∣≥0.8]≤2e−2×0.82×10≈5.5215451440744015×10−6Hoeffding:\mathbb P[| \mu-v|>\epsilon]\le 2e^{-2\epsilon ^2N}\\ \begin{aligned} \mathbb P[v\le 0.1] &=P[0.9-v\ge 0.8]\\ &=P[\mu-v\ge 0.8]\\ &\le P[|\mu-v|\ge 0.8]\\ &\le 2e^{-2\times 0.8^2\times 10}\\ &\approx5.5215451440744015\times 10^{-6} \end{aligned}Hoeffding:P[∣μ−v∣>ϵ]≤2e−2ϵ2NP[v≤0.1]=P[0.9−v≥0.8]=P[μ−v≥0.8]≤P[∣μ−v∣≥0.8]≤2e−2×0.82×10≈5.5215451440744015×10−6

- A:奇数绿,偶数橙
- B:奇数橙,偶数绿
- C:1-3橙,4-6绿
- D:1-3绿,4-6橙
5个橙1,只可能是BC中,所以132=8256\frac{1}{32}=\frac{8}{256}321=2568

- 1全橙:BC
- 2全橙:AC
- 3全橙:BC
- 4全橙:AD
- 5全橙:BD
- 6全橙:AD
- 全A,B,C,D被重复算了一遍,要减去4
P=4×25−445=31256P=\frac{4\times2^5-4}{4^5}=\frac {31}{256}P=454×25−4=25631

Question15-PLA

data链接

代码部分:
utils函数:
import numpy as np
#判别函数,判断所有数据是否分类完成
def Judge(X, y, w):n = X.shape[0]num = np.sum(X.dot(w) * y > 0)return num == ndef PLA(X, y, eta=1, max_step=np.inf):# 获取维度n, d = X.shape# 初始化w = np.zeros(d)# 迭代次数t = 0# 元素的下标i = 0# 错误的下标last = 0while not (Judge(X, y, w)) :if np.sign(X[i, :].dot(w) * y[i]) <= 0:t += 1w += eta * y[i] * X[i, :]# 更新错误last = i# 移动到下一个元素,如果达到n,则重置为0i += 1if i == n:i = 0return t, last, w
主函数:
import numpy as np
import utils as util#读取数据
data = np.genfromtxt("hw1_15_train.dat")
#获取维度
n, d = data.shape
#分离X
X = data[:, :-1]
#添加偏置项1
X = np.c_[np.ones(n), X]
#分离y
y = data[:, -1]
print(util.PLA(X, y))
运行结果:

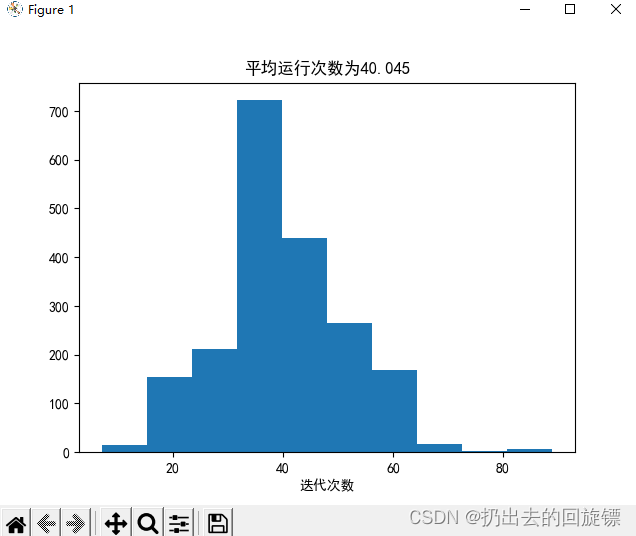
Question16-PLA平均迭代次数

代码部分:
utils函数:
import numpy as np
import matplotlib.pyplot as pltdef Judge(X, y, w):n = X.shape[0]num = np.sum(X.dot(w) * y > 0)return num == ndef PLA(X, y, eta=1):n, d = X.shapew = np.zeros(d)t = 0i = 0last = 0while not (Judge(X, y, w)):if np.sign(X[i, :].dot(w) * y[i]) <= 0:t += 1w += eta * y[i] * X[i, :]last = ii += 1if i == n:i = 0return t, last, w#运行g算法n次并返回平均的迭代次数
def average_of_n(g, X, y, n, eta=1):result = []data = np.c_[X, y]for i in range(n):np.random.shuffle(data)X = data[:, :-1]y = data[:, -1]result.append(g(X, y, eta=eta)[0])plt.hist(result)plt.xlabel("迭代次数")plt.title("平均运行次数为" + str(np.mean(result)))plt.show()
主函数:
import numpy as np
import utils as util
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签
plt.rcParams['axes.unicode_minus']=False #显示负号data = np.genfromtxt("hw1_15_train.dat")
#获取维度
n, d = data.shape
#分离X
X = data[:, :-1]
#添加偏置项1
X = np.c_[np.ones(n), X]
#分离y
y = data[:, -1]
util.average_of_n(util.PLA, X, y, 2000, 1)
Question17-不同迭代系数的PLA
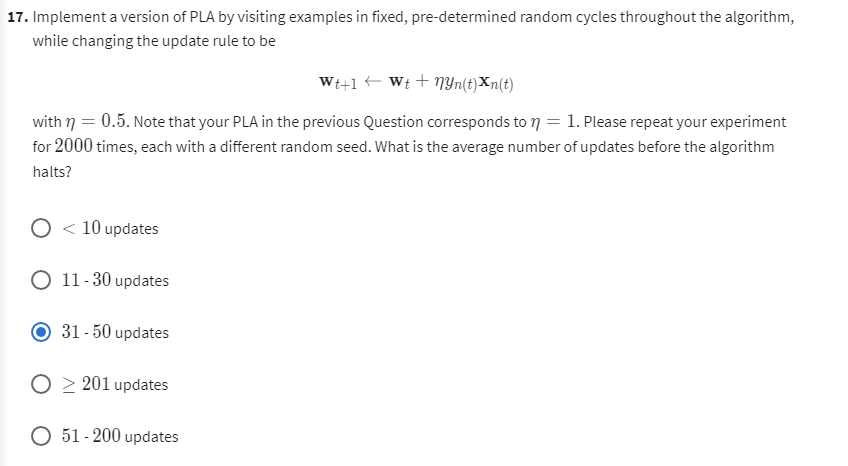
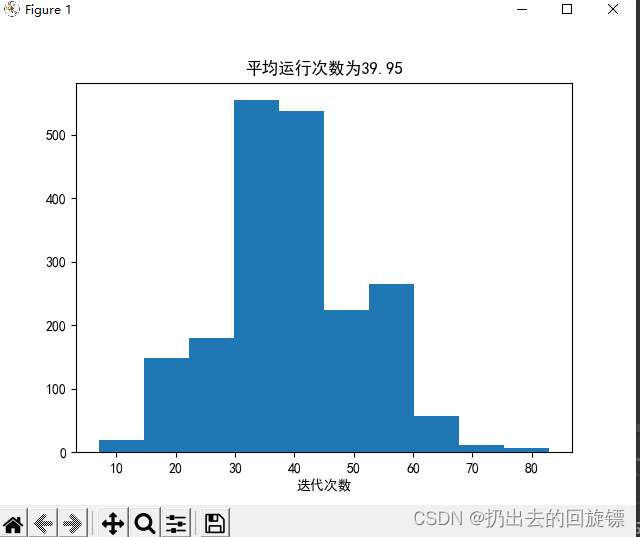
修改迭代系数即可:
util.average_of_n(util.PLA, X, y, 2000, 0.5)
Question18-Pocket_PLA
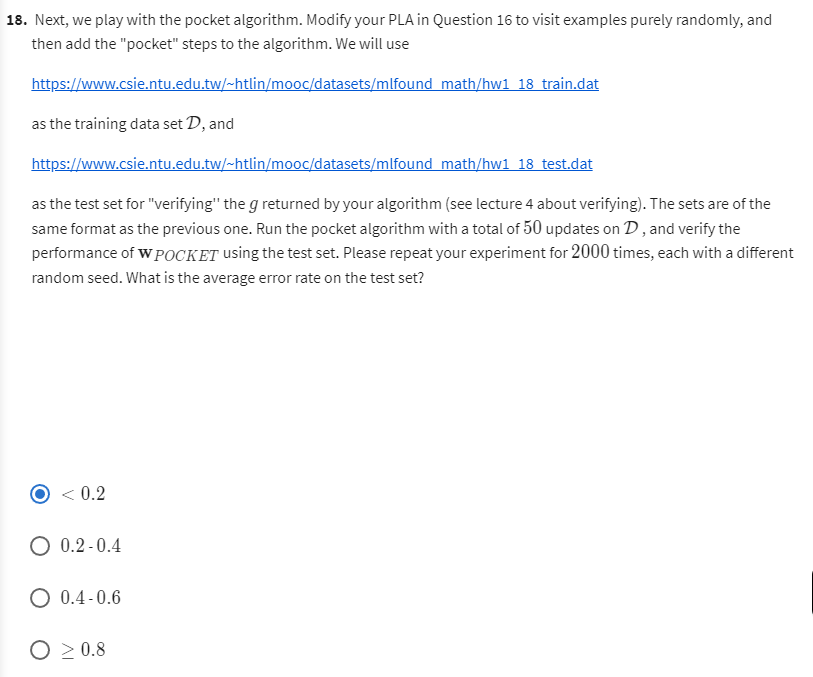
utils函数:
import matplotlib.pyplot as plt
import numpy as np
#统计错误数量
def count(X, y, w):num = np.sum(X.dot(w) * y <= 0)return np.sum(num)#预处理
def preprocess(data):# 获取维度n, d = data.shape# 分离XX = data[:, :-1]# 添加偏置项1X = np.c_[np.ones(n), X]# 分离yy = data[:, -1]return X, ydef Pocket_PLA(X, y, eta=1, max_step=np.inf):#max_step 限制迭代次数#获得数据维度n, d = X.shape#初始化w = np.zeros(d)#记录最优向量w0 = np.zeros(d)#记录次数t = 0#记录最少错误数量error = count(X, y, w0)#记录元素的下标i = 0while (error != 0 and t < max_step):if np.sign(X[i, :].dot(w) * y[i]) <= 0:w += eta * y[i] * X[i, :]#迭代次数增加t += 1#记录当前错误error_now = count(X, y, w)if error_now < error:error = error_noww0 = np.copy(w)#移动到下一个元素i += 1#如果达到n,则重置为0if i == n:i = 0return error, w0#运行g算法n次,1代表训练集,2代表测试集
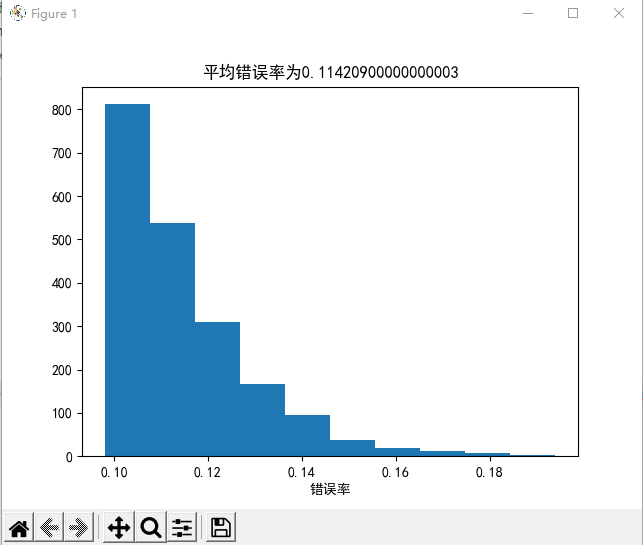
def average_of_n(g, X1, y1, X2, y2, n, eta=1, max_step=np.inf):result = []data = np.c_[X1, y1]m = X2.shape[0]for i in range(n):np.random.shuffle(data)X = data[:, :-1]y = data[:, -1]w = g(X, y, eta=eta, max_step=max_step)[-1]result.append(count(X2, y2, w) / m)plt.hist(result)plt.xlabel("错误率")plt.title("平均错误率为"+str(np.mean(result)))plt.show()
主函数:
import matplotlib.pyplot as plt
import numpy as np
import utils as util
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号data_train = np.genfromtxt("hw1_18_train.dat")
data_test = np.genfromtxt("hw1_18_test.dat")X_train, y_train = util.preprocess(data_train)
X_test, y_test = util.preprocess(data_test)util.average_of_n(util.Pocket_PLA, X_train, y_train, X_test, y_test, 2000, max_step=50)
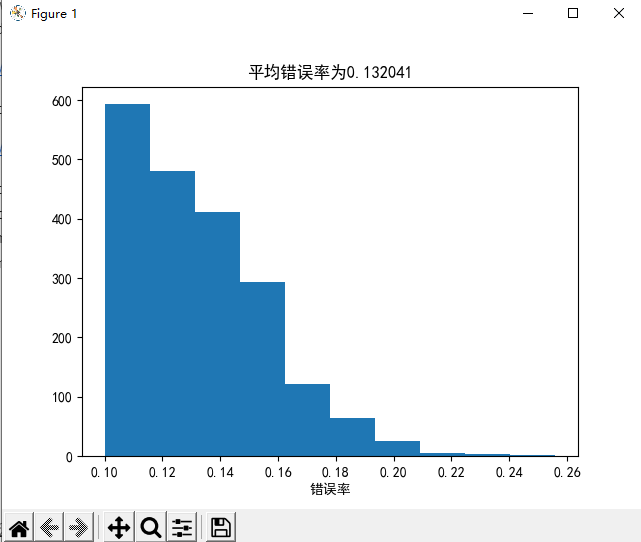
Question19-PLA的错误率

utils函数:
import matplotlib.pyplot as plt
import numpy as npdef count(X, y, w):#判断是否同号num = np.sum(X.dot(w) * y <= 0)return np.sum(num)def Judge(X, y, w):n = X.shape[0]#判断是否同号num = np.sum(X.dot(w) * y > 0)return num == ndef preprocess(data):"""数据预处理"""# 获取维度n, d = data.shape# 分离XX = data[:, :-1]# 添加偏置项1X = np.c_[np.ones(n), X]# 分离yy = data[:, -1]return X, ydef PLA(X, y, eta=1,max_step=np.inf):n, d = X.shapew = np.zeros(d)t = 0i = 0last = 0while not (Judge(X, y, w)) and t<max_step:if np.sign(X[i, :].dot(w) * y[i]) <= 0:t += 1w += eta * y[i] * X[i, :]last = ii += 1if i == n:i = 0return t, last, w#运行g算法n次,1代表训练集,2代表测试集
def average_of_n(g, X1, y1, X2, y2, n, eta=1, max_step=np.inf):result = []data = np.c_[X1, y1]m = X2.shape[0]for i in range(n):np.random.shuffle(data)X = data[:, :-1]y = data[:, -1]w = g(X, y, eta=eta, max_step=max_step)[-1]result.append(count(X2, y2, w) / m)plt.hist(result)plt.xlabel("错误率")plt.title("平均错误率为"+str(np.mean(result)))plt.show()
主函数:
import matplotlib.pyplot as plt
import numpy as np
import utils as util
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号data_train = np.genfromtxt("hw1_18_train.dat")
data_test = np.genfromtxt("hw1_18_test.dat")X_train, y_train = util.preprocess(data_train)
X_test, y_test = util.preprocess(data_test)util.average_of_n(util.PLA, X_train, y_train, X_test, y_test, 2000, max_step=50)
Question20-修改Pocket_PLA迭代次数
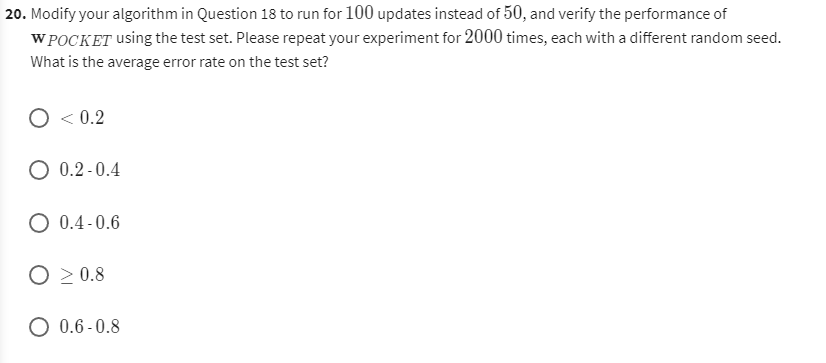
utils函数:
import matplotlib.pyplot as plt
import numpy as npdef count(X, y, w):#判断是否同号num = np.sum(X.dot(w) * y <= 0)return np.sum(num)def Judge(X, y, w):n = X.shape[0]#判断是否同号num = np.sum(X.dot(w) * y > 0)return num == ndef preprocess(data):"""数据预处理"""# 获取维度n, d = data.shape# 分离XX = data[:, :-1]# 添加偏置项1X = np.c_[np.ones(n), X]# 分离yy = data[:, -1]return X, ydef Pocket_PLA(X, y, eta=1, max_step=np.inf):#max_step 限制迭代次数#获得数据维度n, d = X.shape#初始化w = np.zeros(d)#记录最优向量w0 = np.zeros(d)#记录次数t = 0#记录最少错误数量error = count(X, y, w0)#记录元素的下标i = 0while (error != 0 and t < max_step):if np.sign(X[i, :].dot(w) * y[i]) <= 0:w += eta * y[i] * X[i, :]#迭代次数增加t += 1#记录当前错误error_now = count(X, y, w)if error_now < error:error = error_noww0 = np.copy(w)#移动到下一个元素i += 1#如果达到n,则重置为0if i == n:i = 0return error, w0#运行g算法n次,1代表训练集,2代表测试集
def average_of_n(g, X1, y1, X2, y2, n, eta=1, max_step=np.inf):result = []data = np.c_[X1, y1]m = X2.shape[0]for i in range(n):np.random.shuffle(data)X = data[:, :-1]y = data[:, -1]w = g(X, y, eta=eta, max_step=max_step)[-1]result.append(count(X2, y2, w) / m)plt.hist(result)plt.xlabel("错误率")plt.title("平均错误率为"+str(np.mean(result)))plt.show()
主函数:
import matplotlib.pyplot as plt
import numpy as np
import utils as util
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号data_train = np.genfromtxt("hw1_18_train.dat")
data_test = np.genfromtxt("hw1_18_test.dat")X_train, y_train = util.preprocess(data_train)
X_test, y_test = util.preprocess(data_test)util.average_of_n(util.Pocket_PLA, X_train, y_train, X_test, y_test, 2000, max_step=100)