当前位置：首页 > news >正文

C++基础算法④——排序算法(快速、归并附完整代码)

news 2025/7/19 8:27:35

快速排序

快速排序是对冒泡排序的一种改进。
它的基本思想是:通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录继续进行快速排序，以达到整个序列有序。
假设我们现在对 6 1 2 7 9 3 4 5 1 0 8 这个10个数进行排序。

int main(){int n;cin>>n;for(int i=1;i<=n;i++) cin>>a[i];qsort(1,n);for(int i=1;i <=n;i++){cout<<a[i]<<" ";}	return 0;
}

首先在这个序列中随便找一个数作为基准数(不要被这个名词吓到了，就是一个用来参照的数)。为了方便，就让第一个数6作为基准数吧。接下来，需要将这个序列中所有比基准数大的数放在6的右边，比基准数小的数放在6的左边，类似下面这种排列:

int a[10001];
void qsort(int l,int r){int i,j,mid;i=l+1,j=r;mid=a[l];

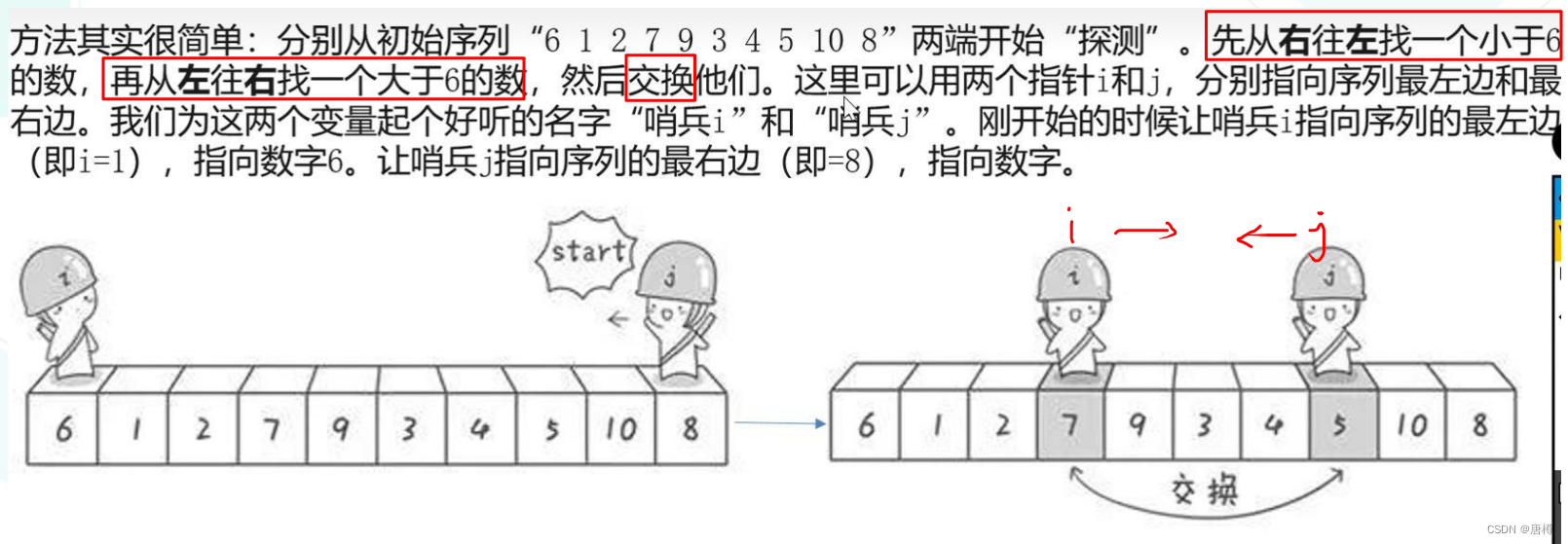
在这里插入图片描述
可以发现，i从第二个位置开始，j从最后一个位置开始；当 i 指向的值大于基准值6 而且当 j 指向的值小于基准值6，就把这两个值交换，然后接着往下继续比。

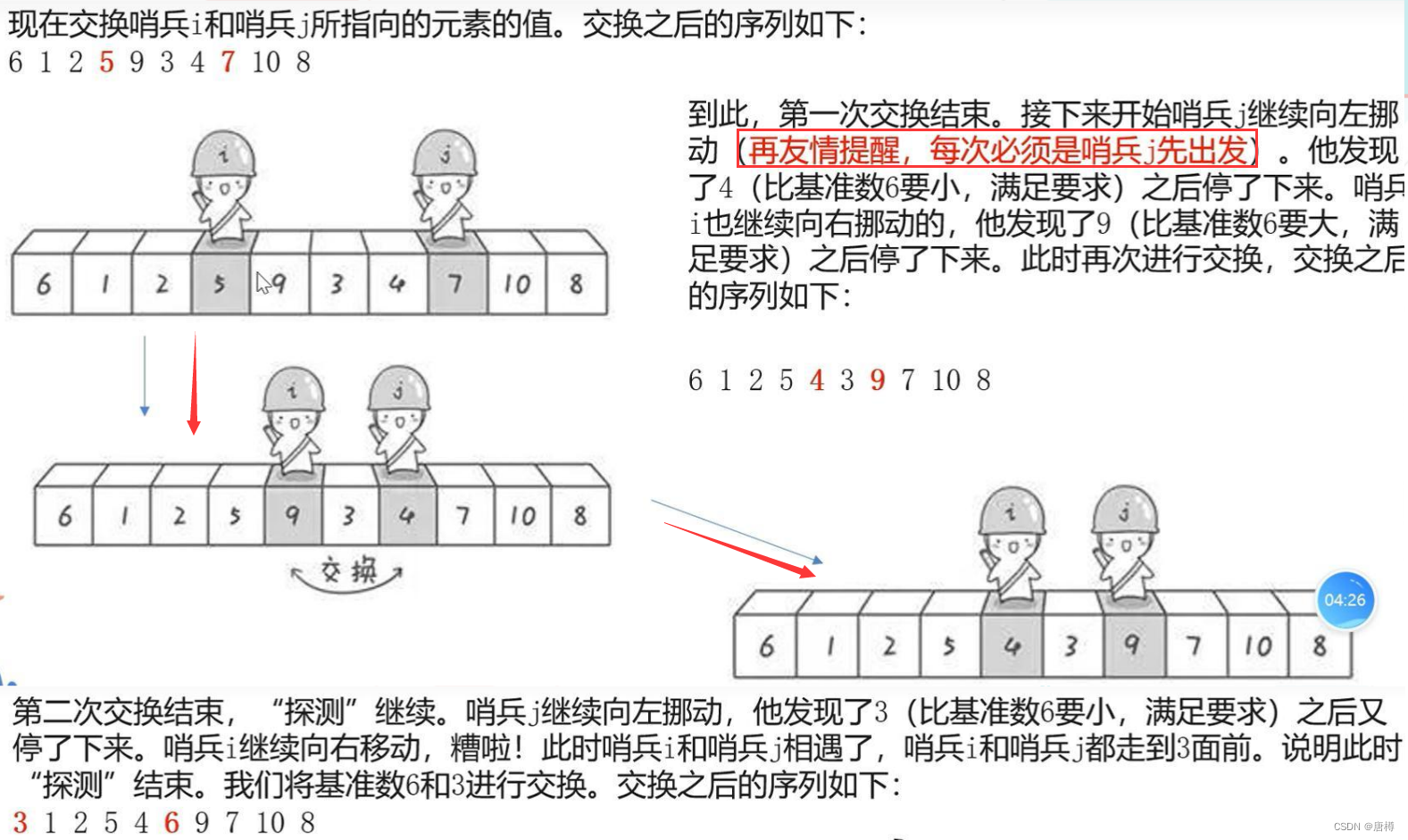
while(i<=j){ //当 i j 没有碰到while(a[i]<mid) i++;while(a[j]>mid) j--;if(i<=j){swap(a[i],a[j]);i++; j--;}}

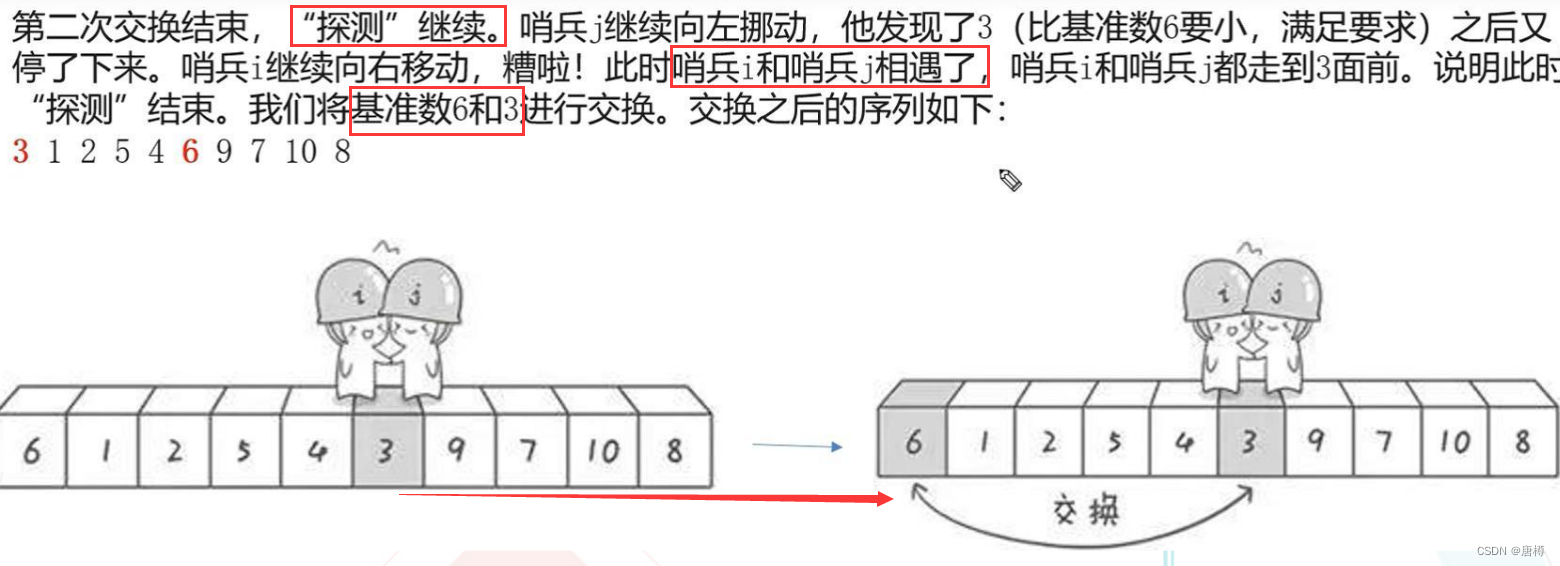
在这里插入图片描述
当 i j 相遇了，就把 j指向的值与基准数交换。

swap(a[j],a[l]); //交换基准数

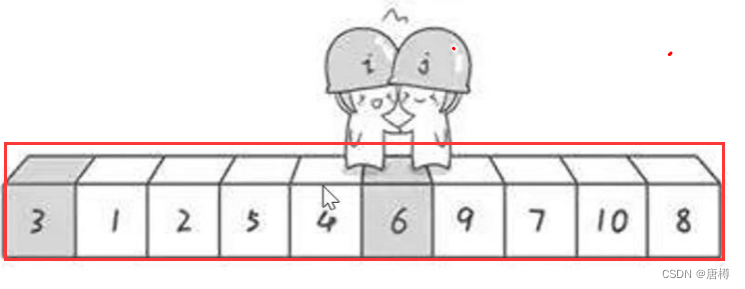
在这里插入图片描述
可以发现，一趟完毕，原基准数6的左边值一定比6小，右边比6大。这样就确定了基准数6的排序。
接下来，对于6左边的序列3 1 2 5 4和右边的序列9 7 10 8分别进行快速排序。
把整体分了左右边，再把左边的序列3 1 2 5 4看成新的重新进行快速排序。不断地分解。
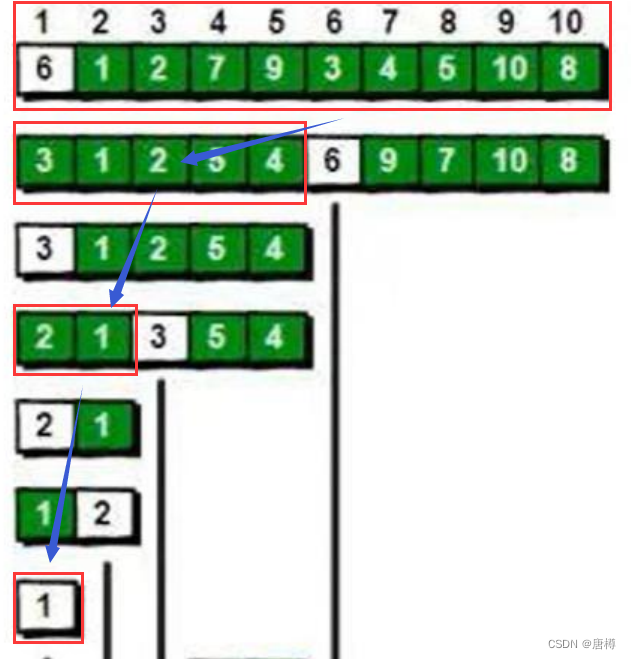
在这里插入图片描述
所以这个排序运用了分治的思想！
完整代码：

#include<bits/stdc++.h>
using namespace std;
int a[10001];
void qsort(int l,int r){int i,j,mid;i=l+1,j=r;mid=a[l];while(i<=j){while(a[i]<mid) i++;while(a[j]>mid) j--;if(i<=j){swap(a[i],a[j]);i++; j--;}}swap(a[j],a[l]); //交换基准数if(l<j) qsort(l,j-1);if(i<r) qsort(i,r); 
}
int main(){int n;cin>>n;for(int i=1;i<=n;i++) cin>>a[i];qsort(1,n);for(int i=1;i <=n;i++){cout<<a[i]<<" ";}	return 0;
}

快速排序是不稳定的排序方法，时间复杂度是O(nlog2n)，速度快，平均时间来说，快速排序是最好的一种内部排序方法。但快速排序需要一个栈空间实现递归，每一趟排序都会将记录序列分割成两个子序列，栈最大深度为log(n+1)。

归并排序

归并的思路（分治）是把一个大问题a拆解成两个小问题b和c，解决了两个子问题再整合一下，就解决了原问题。用递归的方法，先分解再合并（分治是一种解决问题的处理思想，递归是一种编程技巧，这两者并不冲突）。

稳定性：稳定；
空间复杂度O(n)；
复杂度：时间复杂度O(nlogn)；
优缺点：效率高且稳定，但是消耗的辅助空间与原数据空间成正比。

int main(){cin>>n;for(int i=1;i<=n;i++){ //输入 cin>>a[i];}//归并排序mergesort(1,n);for(int i=1;i<=n;i++){ //输出 cout<<a[i]<<" ";}return 0;
}

递归分解

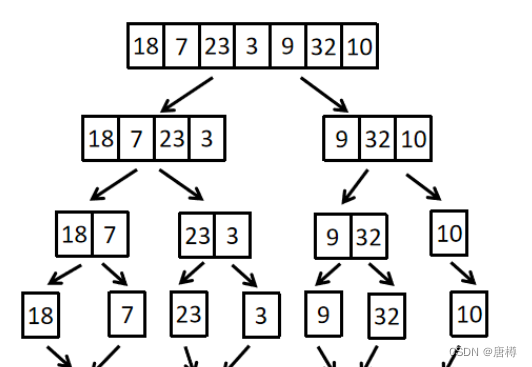
不断地二分分解，拆左右。

void mergesort(int l,int r){int mid = (l+r)/2;if(l==r) return ;mergesort(l,mid); //左边排序mergesort(mid+1,r);//右边排序//上面已经拆成一个一个 merge(l,mid,mid+1,r); //合并操作 
}

分解到1个值，然后再合并排序。合并的思路看成：左边是有序的a数组；右边是有序的b数组。两数组开始比较，小的值依次存到c数组。

int a[100],c[100],n,cnt;
void merge(int left,int i,int j,int right){int lenc = left;int len1 = left;  //左边开头 看成a[] int len2 = j;  	//右边开头	 看成b[] while(len1<=i && len2<=right){ //并c[] if(a[len1]<a[len2]){ //左边小于右边 c[lenc++] = a[len1++];}else{//右边小于左边c[lenc++] = a[len2++];}} while(len1<=i){c[lenc++] = a[len1++];} while(len2<=right){c[lenc++] = a[len2++];}//把排好序的c数组存回a数组里面for(int k=left;k<=right;k++){a[k]=c[k];} 
}

完整代码：

#include<bits/stdc++.h>
using namespace std;
int a[100],c[100],n,cnt;
void merge(int left,int i,int j,int right){int lenc = left;int len1 = left;  //左边开头 看成a[] int len2 = j;  	//右边开头	 看成b[] while(len1<=i && len2<=right){ //并c[] if(a[len1]<a[len2]){ //左边小于右边 c[lenc++] = a[len1++];}else{//右边小于左边c[lenc++] = a[len2++];}} while(len1<=i){c[lenc++] = a[len1++];} while(len2<=right){c[lenc++] = a[len2++];}//把排好序的c数组存回a数组里面for(int k=left;k<=right;k++){a[k]=c[k];} 
} void mergesort(int l,int r){int mid = (l+r)/2;if(l==r) return ;mergesort(l,mid); //左边排序mergesort(mid+1,r);//右边排序//上面已经拆成一个一个 merge(l,mid,mid+1,r); //合并操作 
}
int main(){cin>>n;for(int i=1;i<=n;i++){ //输入 cin>>a[i];}//归并排序mergesort(1,n);for(int i=1;i<=n;i++){ //输出 cout<<a[i]<<" ";}return 0;
}