当前位置：首页 > news >正文

NEFU离散数学实验3-递推方程

news 2025/9/6 15:15:05

相关概念

递推方程是指一种递归定义，它将问题拆分成更小的子问题，并使用这些子问题的解来计算原问题的解。离散数学中，递推方程通常用于描述数列、组合问题等。

以下是一些递推方程相关的概念和公式：

1. 递推公式：递推公式是指将一个问题拆分成更小的子问题，并使用这些子问题的解来计算原问题的解的公式。通常用于描述数列。

2. 初始条件：递推公式需要初始条件来确定数列的起始值。例如，斐波那契数列的初始条件是前两个数为0和1。

3. 递推关系式：递推关系式是指描述一个问题中相邻两项之间的关系的公式。例如，斐波那契数列的递推关系式为f(n) = f(n-1) + f(n-2)。

4. 通项公式：通项公式是指将递推公式表示为一个包含n的表达式，直接计算第n项的值。例如，斐波那契数列的通项公式为 $f(n) = \frac{1}{\sqrt{5}}\left(\frac{1+\sqrt{5}}{2}\right)^n - \frac{1}{\sqrt{5}}\left(\frac{1-\sqrt{5}}{2}\right)^n$

5. 逆向递推：逆向递推是指从已知的数列末项倒推出数列的初始项。通常可使用通项公式或递推公式进行逆向递推。

6. 生成函数：生成函数是一种将一个数列表示为一个形式幂级数的函数。可以利用生成函数求解数列的各种性质和问题。

1. (程序题)江城子

古诗词的平仄规律平仄,是中国诗词中用字的声调。平指平直,仄指曲折，而苏轼在写宋词的时候将其划分为3种，平，上仄和下仄；而一句词是有效的当且仅当这句词中含有偶数个“平”；现在让你计算n位长的词是有效的话有多少种声调？---------“十年生死两茫茫，不思量，自难忘”！

注意：0是偶数

Input

输入数据只有1组，一个整数n(1<=n<=20);

Output

对于输入的数据n,输出本题答案

Sample Input

2

Sample Output

5

#include <iostream>
#include <cmath>
using namespace std;int main() {int n; // n为指数;cin >> n;long long  sum = pow(3, n); // 调用pow()函数求解3的n次方long long result = (1 + sum) / 2;cout << result;return 0;
}

2. (程序题)涂格子

一个1*n的方格用红、蓝、绿或橙色四种颜色涂色，如果有偶数个方格被涂成红色，还有偶数个方格被涂成绿色，问有多少种方案？（15分）

Input

输入数据有多组，每组有1个正整数n(1<=n<=10),代表方格的个数。

Output

在一行内输出有多少种方案？

Sample Input

1

Sample Output

2

#include <iostream>
#include <cmath>
using namespace std;int main() {int n; // n为指数;while(cin>>n){long long  sum1 = pow(4, n - 1);long long  sum2 = pow(2, n - 1);long long result;if(n == 0)result = 1 ;elseresult = sum1 + sum2 ;cout << result << endl;}return 0;
}

3. (程序题) fibonacci数列

fibonacci数列定义为 1 1 2 3 5 8 ......;

f(n)=f(n-1)+f(n-2); f(0)=1;f(1)=1;

现在请你计算第n个该数列的长度是多少？（就是求f(n)的位数）

输入数据只有1组，一个数n(1<=n<=1000000)

输出f(n)的位数即可！

例子输入；

2

例子输出

1

#include <iostream>#include <cmath>using namespace std;int main(){int n;double x,sum;cin>>n;x=log10((1+sqrt(5))/2);sum=x*n;cout<<int(sum)+1<<endl;return 0;}

4. (程序题) 信息编码

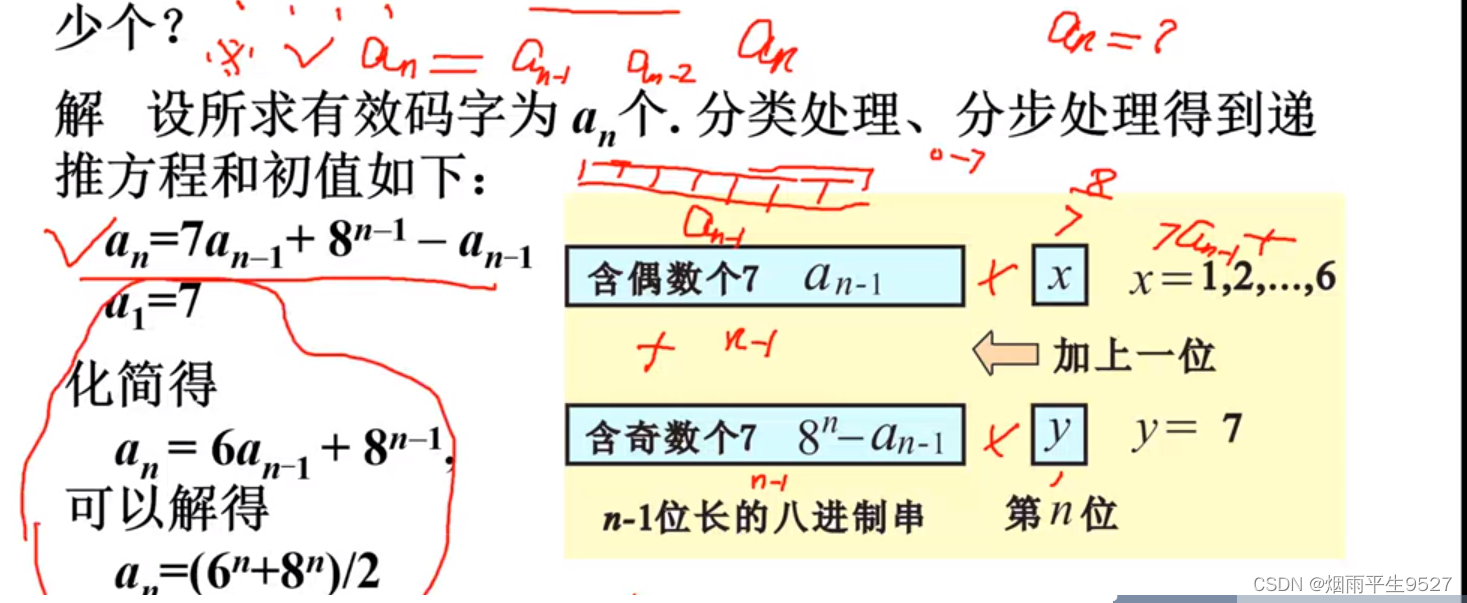
一个编码系统用八进制数字对信息编码，一个码字是有效的当且仅当含有偶数个7，求n位长的有效码字有多少个？（10分）

Input

输入数据有多组，每组有1个正整数n(1<=n<=10),代表编码的长度。

Output

在一行内输出n位长的有效码字有多少个？

Sample Input

1

Sample Output

7

#include <iostream>#include <cmath>using namespace std;int main() {int n; // n为指数;while(cin >> n){long long  sum1 = pow(6, n);long long  sum2 = pow(8, n);long long result = (sum1 + sum2) / 2;cout << result<<endl;}return 0;}