堆-----数据结构
引言
什么是堆?堆是一种特殊的数据结构(用数组表示的树)。
为什么要使用到堆?比如一场比赛,如果使用擂台赛的方式来决出冠军(实力第一),就很难知道实力第二的队伍是什么了。
但是下图能很清楚的表示各队伍的强弱关系。
堆的特点
上图就是一个最大堆,解释:每一个圆都是一个节点,数字代表着键值,其中95是93和92的父节点,93和92是95的子节点,93和92是兄弟节点(父节点为同一个),根节点就是键值最大的节点,为95,最后一个节点是87,最后一个左子节点也是87。
最大堆的特点:
满足以下三点
1.每个节点最多可以有两个子节点。
2.根节点的键值是所有堆节点键值中最大者,且每个节点的值都大于其子(孩子)节点。
3.除了根节点没有兄弟节点,最后一个左子节点可以没有兄弟节点,其他节点必须有兄弟节点。
最好是自己理解,不用强记 。其中有一点要注意:A的兄弟节点的子节点可能大于A,相当于在比赛中,其中一个小组都是弱队,那么一个弱队却可以闯入半决赛一样。
最小堆的特点的话就将第二点中的大改为小就可以了,其他的特点一样。这里讨论的是最大堆
数组形式表示
父节点和子节点的关系:
i 的左子节点:2i+1 ,右子节点:2i+2
i 的父节点:(i-1)/2
i 是从 0 开始的
再将上图的堆转换为数组的形式,如下图:

这就是一个最大堆的数组表示形式。
在数组中快速创建堆
也就是怎么把任意一个数组变成最大/小堆。
我们先把堆的最小单位拿出来,如下图:
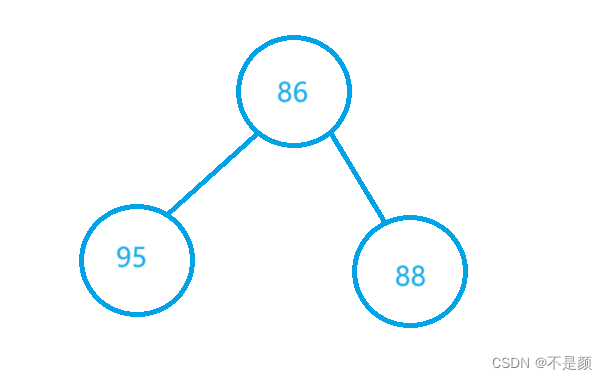
他不是一个最大堆,如果要变成最大堆,只需要父节点是95,子节点分别是86、88就可以了(86和95交换)。而一个最大堆是由若干个这个最小单位组成的,所以第一步就是将所有的堆的最小单位变成最大堆。
1、首先先找到最后一个节点的父节点,找出该节点的最大子节点与自己比较,如果大于自身,就交换两个节点。
2、继续移动到上一个父节点(也就是下标 -1 的地方),重复做第一步的比较操作,直到遍历所有的父节点。
当我们移动完所有的父节点,那最大堆就形成了吗?还疏忽了一个地方。例如当移动到某个父节点时,如下图:
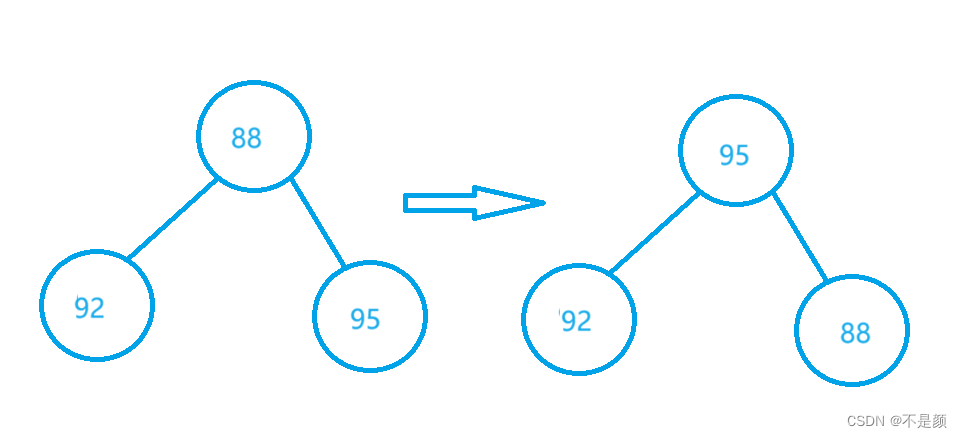
最开始父节点是88,与子节点95交换了,那父节点就是95,95 的子节点就是 88,那88一定大于他的子节点吗?很显然这个答案是不一定,因为 88 的子节点只满足小于之前的父节点 95,所以还需要向下调整,直到子节点都小于父节点。
3、对每次移动中,变成子节点的节点,向下调整,也就是判断他与子节点是否满足最大堆的特点,不满足还要继续移动节点(向下调整),满足的话就接着下个父节点。
4、所有的节点交换完毕,最大堆构建完成。
堆的算法实现
堆数据结构的定义
#define DEFAULT_CAPCITY 120 //默认的堆容量typedef struct _Heap
{int* arr; //存储堆元素的数组int size; //堆中元素的个数int capcity; //堆的容量
}Heap;//函数声明
void buildHeap(Heap& heap);
bool inset(Heap& heap, int value);
bool initHeap(Heap& heap, int* orginal, int size);
void adjustDown(Heap& heap, int i);
void adjustUp(Heap& heap, int i);堆的初始化
bool initHeap(Heap& heap,int *orginal,int size)
{//orginal 是指向数组的指针,而这个数组是我们要传入堆的数组int capcity = DEFAULT_CAPCITY > size ? DEFAULT_CAPCITY : size; //取size和默认容量的最大值heap.arr = new int[capcity];if (!heap.arr) return false; //申请失败heap.capcity = capcity;if (size > 0) //size合法{memcpy(heap.arr, orginal, sizeof(int) * size);heap.size = size;//建堆buildHeap(heap);}return true;
}堆的创建
//建堆,从最后一个父节点逐个向前调整所有的父节点(直到根节点),确保每一个父节点都是一个最大堆
//那么,整体上就是一个最大堆
void buildHeap(Heap& heap)
{int i = (heap.size - 2) / 2; //因为下标从0开始,heap.size-1就得到下标,再结合公式就是这个式子for (; i >= 0; i--){adjustDown(heap, i); //向下调整包含了构建最大堆,如果感到困惑,先看向下调整函数}
}堆的向下调整函数
void adjustDown(Heap& heap, int i)
{int temp = heap.arr[i]; //保存父节点的键值int parent = 0 ,child = 0;for (parent = i; (2 * parent + 1) < heap.size; parent = child) {child = 2 * parent + 1; //先指向左子节点//指向两个子节点中最大的节点if (child + 1 < heap.size && heap.arr[child] < heap.arr[child + 1]){child = child + 1;}if (temp >= heap.arr[child]){break; //无需向下调整}else{heap.arr[parent] = heap.arr[child];heap.arr[child] = temp;}}
}堆的插入新元素
1、插入新的元素到最大堆的尾部,也就是数组的后面
2、插入的元素可能会破环这个最大堆,需要重新调整,和父节点比较,如果比父节点大,就交换两个节点……重复直到新节点比父节点小或者新节点变为根节点(调整到位)。
设计两个函数,一个是插入,一个是向上调整。
bool insert(Heap& heap, int value)
{if (heap.size == heap.capcity) //堆空间不足{return false;}int i = heap.size ; //指向新加元素的下标heap.arr[heap.size++] = value;adjustUp(heap , i);return true;
}void adjustUp(Heap& heap, int i)
{if (i <= 0 || i >= heap.size) return;while (i > 0){int parent = (i - 1) / 2;if (parent >= 0) // 父节点没越界{if (heap.arr[parent] < heap.arr[i]){int temp = heap.arr[i];heap.arr[i] = heap.arr[parent];heap.arr[parent] = temp;i = parent;}else{break; //无需调整}}else{break; //父节点出界}}
}看到这,你会发现堆的创建还有一种方式,也就是将数组的元素一个一个插入,也能得到最大堆。
源代码
#include <iostream>using namespace std;#define DEFAULT_CAPCITY 120 //默认的堆容量typedef struct _Heap
{int* arr; //存储堆元素的数组int size; //堆中元素的个数int capcity; //堆的容量
}Heap;void buildHeap(Heap& heap);
bool insert(Heap& heap, int value);
bool initHeap(Heap& heap, int* orginal, int size);
void adjustDown(Heap& heap, int i);
void adjustUp(Heap& heap, int i);//初始化堆
bool initHeap(Heap& heap,int *orginal,int size)
{//orginal 是指向数组的指针,而这个数组是我们要传入堆的数据int capcity = DEFAULT_CAPCITY > size ? DEFAULT_CAPCITY : size; //取size和默认容量的最大值heap.arr = new int[capcity];if (!heap.arr) return false;heap.capcity = capcity;if (size > 0){memcpy(heap.arr, orginal, sizeof(int) * size);heap.size = size;//建堆buildHeap(heap);}return true;
}//建堆,从最后一个父节点逐个向前调整所有的父节点(直到根节点),确保每一个父节点都是一个最大堆
//那么,整体上就是一个最大堆
void buildHeap(Heap& heap)
{int i = (heap.size - 2) / 2; //因为下标从0开始,heap.size-1就得到下标for (; i >= 0; i--){adjustDown(heap, i);}
}void adjustDown(Heap& heap, int i)
{int temp = heap.arr[i]; //父节点的键值int parent = 0 ,child = 0;for (parent = i; (2 * parent + 1) < heap.size; parent = child){child = 2 * parent + 1;//指向两个子节点中最大的节点if (child + 1 < heap.size && heap.arr[child] < heap.arr[child + 1]){child = child + 1;}if (temp >= heap.arr[child]){break; //无需向下调整}else{heap.arr[parent] = heap.arr[child];heap.arr[child] = temp;}}
}//堆——插入新元素
bool insert(Heap& heap, int value)
{if (heap.size == heap.capcity){return false;}int i = heap.size ;heap.arr[heap.size++] = value;adjustUp(heap , i);return true;
}void adjustUp(Heap& heap, int i)
{if (i <= 0 || i >= heap.size) return;while (i > 0){int parent = (i - 1) / 2;if (parent >= 0) // 父节点没越界{if (heap.arr[parent] < heap.arr[i]){int temp = heap.arr[i];heap.arr[i] = heap.arr[parent];heap.arr[parent] = temp;i = parent;}else{break; //无需调整}}else{break; //父节点出界}}
}
int main(void)
{Heap heap;int orginalArr[] = { 1,2,3,87,93,82,92,86,95 };if (!initHeap(heap, orginalArr, sizeof(orginalArr) / sizeof(int))){cout << "初始化堆失败!" << endl;exit(-1);}for (int i = 0; i < heap.size; i++){printf("%d\n",heap.arr[i]);}puts("");insert(heap, 100);for (int i = 0; i < heap.size; i++){printf("%d\n", heap.arr[i]);}return 0;
}
