第十三届蓝桥杯国赛 C++ B 组 J 题——搬砖(AC)
目录
- 1.搬砖
- 1.题目描述
- 2.输入格式
- 3.输出格式
- 4.样例输入
- 5.样例输出
- 6.数据范围
- 7.原题链接
- 2.解题思路
- 3.Ac_code
1.搬砖
1.题目描述
这天,小明在搬砖。
他一共有 nnn 块砖, 他发现第 iii 砖的重量为 wiw_{i}wi, 价值为 viv_{i}vi 。他突然想从这些 砖中选一些出来从下到上堆成一座塔, 并且对于塔中的每一块砖来说, 它上面 所有砖的重量和不能超过它自身的价值。
他想知道这样堆成的塔的总价值(即塔中所有砖块的价值和)最大是多少。
2.输入格式
输入共 n+1n+1n+1 行, 第一行为一个正整数 nnn, 表示砖块的数量。后面 nnn 行, 每行两个正整数 wi,viw_i ,v_iwi,vi
分别表示每块砖的重量和价值。
3.输出格式
一行, 一个整数表示答案。
4.样例输入
5
4 4
1 1
5 2
5 5
4 3
5.样例输出
10
6.数据范围
n≤1000;wi≤20;vi≤20000。n≤1000;w_i ≤20;v_i ≤20000 。n≤1000;wi≤20;vi≤20000。
7.原题链接
搬砖
2.解题思路
诸如此题的模型,思路都是按照一种方式排序,使得最优解答案的选择情况,是排序后的一个子序列,然后直接进行背包 dpdpdp 即可。
那么该如何去寻找排序的条件呢?一般的思路在于,对于砖块 xxx 和 yyy,如果排序后的结果 yyy 在 xxx的后面,那么对于任意 yyy 在 xxx 之上的摆放情况,都一定可以将两者调换。
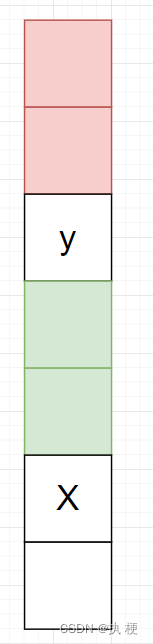
如图,红色砖块为 yyy 上所有砖块的重量,我们设为 w1w_1w1,绿色为 xxx 与 yyy 之间的砖块重量,我们设为 w2w_2w2。
根据题意可知:vy≥w1,vx≥w1+wy+w2v_y≥ w_1,v_x≥w_1+w_y+w_2vy≥w1,vx≥w1+wy+w2,1
假设排序后 yyy 在 xxx 的后面,那么也一定满足:vx≥w1,vy≥w1+wx+w2v_x≥ w_1,v_y≥w_1+w_x+w_2vx≥w1,vy≥w1+wx+w22
因为vx≥w1+wy+w2v_x≥w_1+w_y+w_2vx≥w1+wy+w21且wy+w2w_y+w_2wy+w2一定大于 000,显然vx≥w1v_x≥ w_1vx≥w1是一定符合要求的。
然后考虑第二个式子,因为 vx≥w1+wy+w2v_x≥w_1+w_y+w_2vx≥w1+wy+w21,经过变形可得 vx−wy≥w1+w2v_x-w_y≥w_1+w_2vx−wy≥w1+w23
将式子3带入式子2可得:
vy≥wx+vx−wyv_y≥w_x+v_x-w_yvy≥wx+vx−wy
将式子整理可得:
vy+wy≥wx+vxv_y+w_y≥w_x+v_xvy+wy≥wx+vx
由此,我们找到了排序条件,也就是说,当满足 vy+wy≥wx+vxv_y+w_y≥w_x+v_xvy+wy≥wx+vx 时,任意 yyy 在 xxx 之上的摆放情况,都一定可以将两者调换
接下来就是进行背包 dpdpdp即可,
定义 f[i][j]f[i][j]f[i][j]为只考虑前 iii 个物品,且选择的重量为 jjj 的最大价值。考虑如何进行转移,对于背包问题,无非是选与不选的两种抉择:
f[i][j]={f[i−1][j]不可选max(f[i−1][j],f[i−1][j−w]+v)if j≥w且v≥j-w可选f[i][j] = \begin{cases} f[i-1][j] &不可选\\ max(f[i-1][j],f[i-1][j-w]+v) &\text{if j≥w且v≥j-w} 可选\\ \end{cases}f[i][j]={f[i−1][j]max(f[i−1][j],f[i−1][j−w]+v)不可选if j≥w且v≥j-w可选
题目体积最大只有2e4,答案即为从f[n][0]f[n][0]f[n][0]到 f[n][20000]f[n][20000]f[n][20000]取个最大值。由于是01背包问题,可以使用滚动数组进行优化。
时间复杂度:O(nlogn+nV)O(nlogn+nV)O(nlogn+nV)
3.Ac_code
未优化版本:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s);
#define SZ(s) ((int)s.size());
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 1010;int n;
//只考虑前 i 个砖块,且重量为 j 的最大价值
int f[N][N * 20];
PII a[N];
bool cmp(PII b, PII c) {return b.first + b.second < c.first + c.second;
}
void solve()
{cin >> n;for (int i = 1; i <= n; ++i) {cin >> a[i].first >> a[i].second;}sort(a + 1, a + n + 1, cmp);for (int i = 1; i <= n; ++i) {int w = a[i].first, v = a[i].second;for (int j = 0; j <= 20000; ++j) {f[i][j] = f[i - 1][j];//可选情况if (w <= j && v >= j - w) f[i][j] = max(f[i][j], f[i - 1][j - w] + v);}}int ans=0;for(int i=0;i<=20000;++i) ans=max(ans,f[n][i]);cout << ans << '\n';
}
int main()
{ios_base :: sync_with_stdio(false);cin.tie(0); cout.tie(0);int t = 1;while (t--){solve();}return 0;
}
滚动数组优化:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s);
#define SZ(s) ((int)s.size());
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 1010;int n;
//只考虑前 i 个砖块,且重量为 j 的最大价值
int f[N * 20];
PII a[N];
bool cmp(PII b, PII c) {return b.first + b.second < c.first + c.second;
}
void solve()
{cin >> n;for (int i = 1; i <= n; ++i) {cin >> a[i].first >> a[i].second;}sort(a + 1, a + n + 1, cmp);for (int i = 1; i <= n; ++i) {int w = a[i].first, v = a[i].second;for (int j = 20000; j >= w; --j) {//可选情况if ( v >= j - w) f[j] = max(f[j], f[j - w] + v);}}int ans = 0;for (int i = 0; i <= 20000; ++i) ans = max(ans, f[i]);cout << ans << '\n';
}
int main()
{ios_base :: sync_with_stdio(false);cin.tie(0); cout.tie(0);int t = 1;while (t--){solve();}return 0;
}