论文笔记与复现[156]PARAFAC. tutorial and applications
原文下载:https://www.sciencedirect.com/science/article/abs/pii/S0169743997000324
摘要
本文介绍了PARAFAC的多维分解方法及其在化学计量学中的应用。PARAFAC是PCA向高阶数组的推广,但该方法的一些特性与普通的二维情况截然不同。例如,可以从多维光谱数据(multi-way spectral data)中恢复出纯光谱(pure spectra)。
1 介绍
以交叉方式测量变量,结果的集合为多维数据。
PARAFAC以及二路PCA等方法都是多线性或双线性分解方法,它们将数组分解成分数和负载[16](loadings)的集合,希望以比原始数据数组更精简的形式描述数据。
主成分分析模型可以被认为是最复杂和最灵活的模型,而PARAFAC是最简单和最受限制的模型。
结构越多,拟合越差,模型越简单。使用多维方法不是为了获得更好的拟合,而是为了获得更充分、更稳健和可解释的模型。
对于组分数为F的I×J×K数组,平行因子模型含有F(I+J+K)个参数。
PARAFAC的一个非常令人讨厌的特性是计算模型所需的时间很长。所使用的算法通常基于交替最小二乘法(ALS),ALS的初始化使用随机值或基于广义特征值问题的直接三线性(trilinear)分解。
在下文中,为了简单起见,讨论将仅限于三维(three-way)数据,但大多数结果对任何(更高)阶的数据和模型都有效。
2 术语
标量:小写斜体
矢量:粗体小写
二维矩阵:粗体大写
三维数组:带下划线的粗体大写字母
xijk:X的第ijk个元素
模式(mode)、way和顺序(order)这三个术语或多或少可以互换使用。
术语因子(factor)和组分(component)之间没有区别。
3 模型
数据被分解为三线性分量(三元组,triads),每个分量由一个分数向量和两个负载向量组成。在三维中,通常不区分分数和负载(因为分数和负载在数学上是同等对待的)。
三维数组的平行因子模型由三个负载矩阵A、B、C组成(其中的元素分别表示为aif、bjf、ckf),建立三线性模型以最小化模型中的残差eijk。三维数组的元素可由负载矩阵的元素与残差计算得到,公式如下:
x i j k = ∑ f = 1 F a i f b j f c k f + e i j k ( 1 ) x_{ijk}=\sum_{f=1}^{F}a_{if}b_{jf}c_{kf}\;+e_{ijk} (1) xijk=f=1∑Faifbjfckf+eijk(1)
图1为公式(1)在二组分情况下的计算示意图。
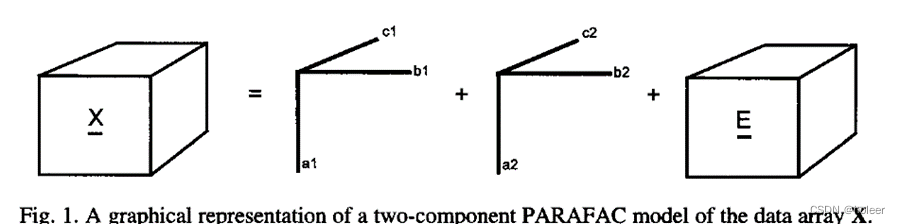
该模型也可记为: X ‾ = ∑ f = 1 F a f ⨂ b f ⨂ c f \underline{X}=\sum_{f=1}^{F}a_f\bigotimes b_f\bigotimes c_f X=f=1∑Faf⨂bf⨂cf
其中af、bf、cf分别为矩阵A、B、C的第f列。
3.1 唯一性
PARAFAC模型的一个明显优点是解的唯一性。如果数据确实是三线性的,使用了正确数量的分量并且信噪比合适,就能得到真正的潜在光谱。
3.2 多维数组的秩(rank)
秩为1的矩阵可以写成2个向量(分数和负载向量)的外积。这样的组成部分被称为二元组。
三元组是二元组的三线性等价物,即三线性(PARAFAC)分量,是3个向量的积。
4 实现
4.1 交替最小二乘法(Alternating least squares)
PARAFAC模型的解可以通过该方法找到,方法是依次假设两种已知模式下的载荷,然后估计最后一种模式的未知参数集。这也是最初提出的对模型进行估计的方式。
PARAFAC ALS算法的流程:
(0)确定组分数F
(1)初始化B和C
(2)通过最小二乘回归,从X, B, C中估计A
(3)用同样的方法估计B
(4)用同样的方法估计C
(5)从步骤(2)开始往下执行,直到收敛。
ALS算法将在每次迭代中改善模型的拟合。如果算法收敛到全局最小值,则找到模型的最小二乘解。
ALS的优点:确保每次迭代都能优化解;ALS的主要缺点:模型估计时间长,当变量数量很多时,有时需要数百到数千次迭代才能收敛。
6 评估解
6.2 杠杆和残差
杠杆和残差可用于影响和残差分析。
6.3 组分数
提取太多的分量不仅意味着噪声被越来越多地建模,而且真实因素被更多(相关)的分量建模。
确定组分数的主要方法有三种:(1)分半实验,(2)判断残差,(3)与建模数据的外部知识进行比较。
[19]主张使用分半实验。其想法是将数据分为两半,然后在这两半上创建PARAFAC模型。通常情况下,应该以具有足够数量的自变量/样本(independent variables/samples)的模式来分割数据。
9 应用II:稀疏荧光数据的唯一分解
9.1 数据
这个问题是PARAFAC使用非负约束获得唯一分解的一个示例。
样品:含有不同量的酪氨酸、色氨酸和苯丙氨酸的2个样品。
因此,要分解的数组是2×51×201。
在多线性分解中应该避免瑞利散射,有三种方法可以做到这一点:(iii)测量空白,并从样品测量值中减去该测量值。在这个实验中,最初没有采取任何措施来消除瑞利散射。
9.2 结果与讨论
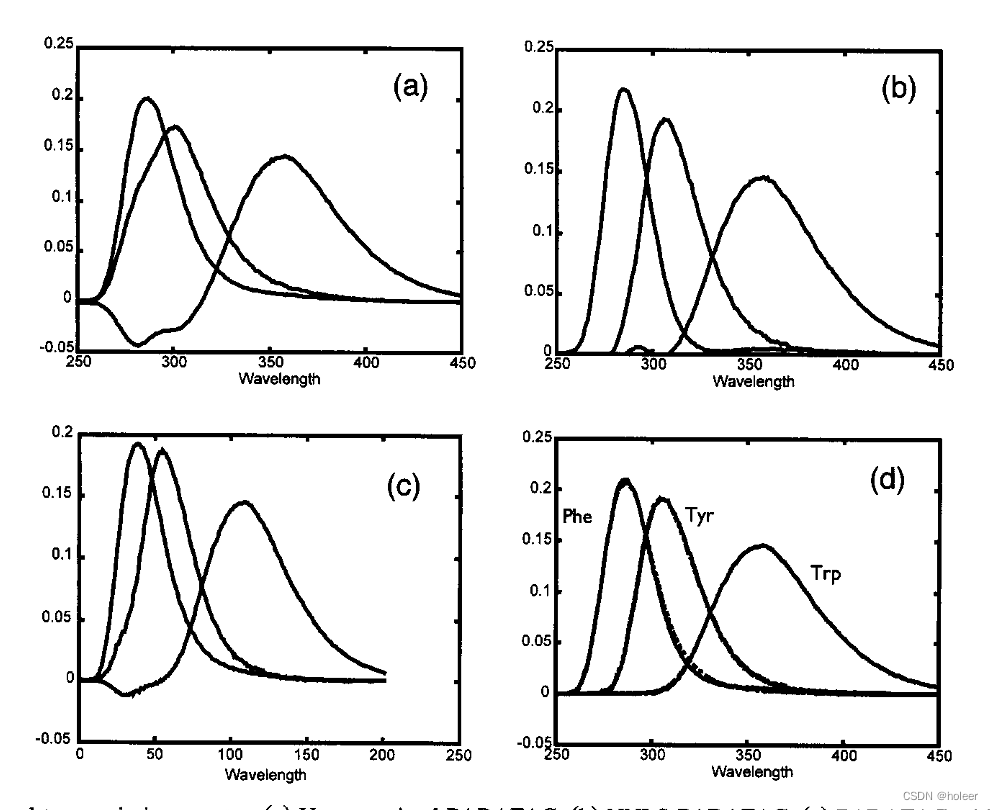
(1)估计的激发光谱如图10(上图)所示。
①三组分PARAFAC溶液的发射负载如图10a所示。从中可以看出,与色氨酸相对应的光谱具有大的负区域。得出的结论是,由于变化性小(两个样品),分解很困难。由于我们知道荧光光谱和浓度应该是正的,所以很自然地将PARAFAC 负载限制在正值 。
②在图10b中,使用非负性约束显示了估计的发射负荷。估计的光谱与分析物的纯光谱非常相似,但对于色氨酸,由于非多重线性瑞利散射,在300mn以下有一个小峰。
③为了避免这种情况,试图将受瑞利散射影响的所有变量设置为缺失值,然后估计相应的PARAFAC模型,结果如图10c所示。
④显然,仅凭这一点不足以确保色氨酸光谱具有良好的曲线分辨率。将缺失元素方法与非负约束相结合,有助于模型关注图中数据的正确方面。在图10d中,估计的发射负载(实线)与纯光谱(虚线,注意区分)一起显示。
(2)估计的激发光谱如图11(下图)所示。
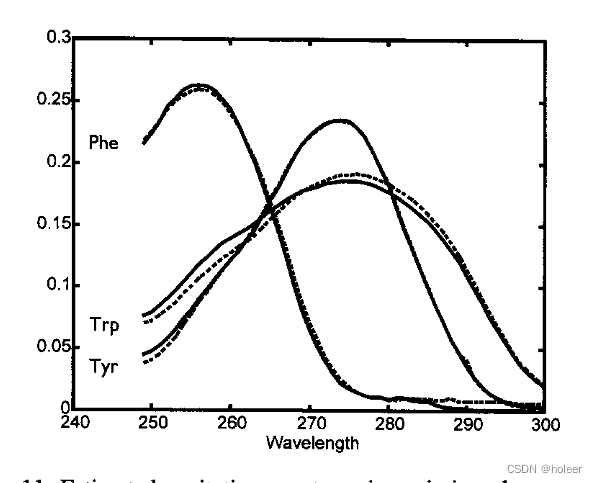
下面使用N-way工具箱的示例数据claus.mat尝试复现图10。
打开Matlab,将数据导入工作区,将EEM数据X重整为520161规格。
绘制5张光谱的填充等高线图:
for i = 1:DimX(1)subplot(2,3,i),contourf(squeeze(X(i,:,:)))
end
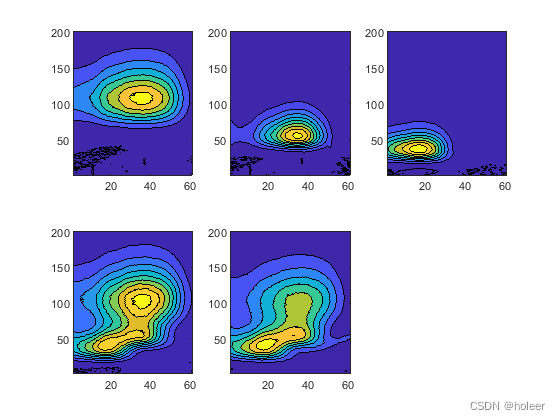
可见,前3张光谱为纯光谱,后2张光谱为混合光谱。
从X中提取第4-5张光谱:P = X(4:5,:,:)
将工作区保存为claus2.mat
[Factors1] = parafac(P,3);
plotfac(Factors1)
下图还原了图10(a):
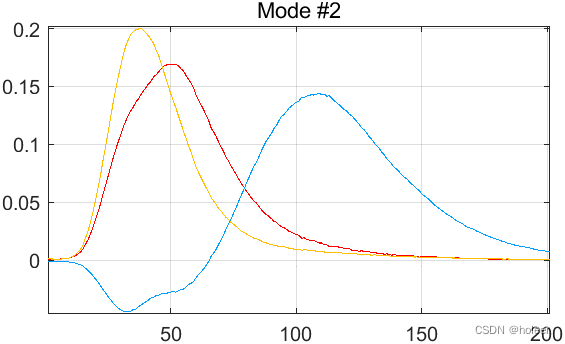
增加非负约束:
[Factors2] = parafac(P,3,0,[2,2,2]);
plotfac(Factors2)
下图还原了图10(b):
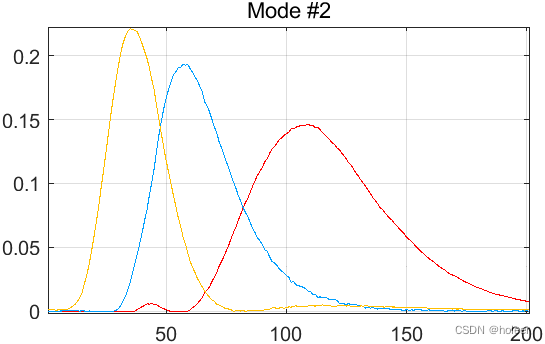
TODO 瑞利散射处理,还原图10c
