随机误差理论与测量
文章目录
- 第1节 随机误差的性质和特点
- 第2节 随机误差的数字特性
- 标准差的估计
- 第3节 单次测量结果的精度指标
- 第4节 多次测量结果的精度指标
- 算数平均值的分布特性与标准差
- 算数平均值的置信度
- 算数平均值的精度指标(常用的有4个)
- 第5节 非等精度测量
第1节 随机误差的性质和特点
随机误差的基本特点:对称性、单峰性、抵偿性、有界性。
随机误差的分布特性:古典误差理论认为:随机误差服从正态分布。其理论依据:中心极限定理。
正态分布及特性:


查分布表时用半边值
第2节 随机误差的数字特性
随机变量的数字特征:
数学期望体现位置特征,方差体现分散性指标。
算术平均值(数学期望的估计)
可以用算数平均值作为真值的估计。
解决了有限次等精度测量中,如何估计被测量真值的问题。

Dx为方差。
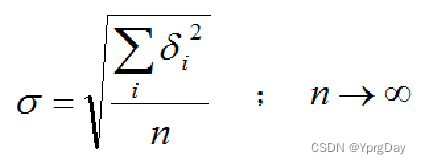
这里的 δ \delta δ 是误差(测量值-真值),而真值是无法得到的,所以要进行标准差的估计方法。
标准差的估计
贝赛尔公式
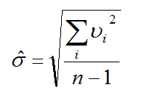
注意这里的 σ \sigma σ是带了帽子的。戴帽子的 σ \sigma σ是不带的无偏估计。
Vi表示的是残差(测量值-平均值),所以是可以得到的。
贝赛尔公式估算条件:测量次数n比较大。
标准偏差的其他估算方法
1)别捷尔斯法(Peters)

2)极差法

dn可查表得到,与测量次数有关(测量n次就查dn):测量的次数越多,ωn大的概率高,故dn应大。极差法可简单迅速算出标准差,n<10时适用。
3) 最大误差法

四种估计方法的优缺点对比
① 贝塞尔公式的计算精度较高,但计算麻烦,需要乘方和开方等,其计算速度难于满足快速自动化测量的需要;
② 别捷尔斯公式最早用于前苏联列宁格勒附近的普尔科夫天文台,它的计算速度较快,但计算精度较低,计算误差为贝氏公式的1.07倍;
③ 用极差法计算σ,非常迅速方便,可用来作为校对公式,当n<10时可用来计算σ,此时计算精度高于贝氏公式;
④ 用最大误差法计算σ更为简捷,容易掌握,当n<10时可用最大误差法,计算精度大多高于贝氏公式,尤其是对于破坏性实验(n=1)只能应用最大误差法。
第3节 单次测量结果的精度指标
正态分布的概率积分——误差函数
标准差σ是表征随机误差很重要的一个特征量,可用于描述测量列中各个测得值的误差。
σs可作为表征测量列中每一个测得值误差的参数。
单次测量是总体中的一次抽样,目前各国多采用以下精度指标:
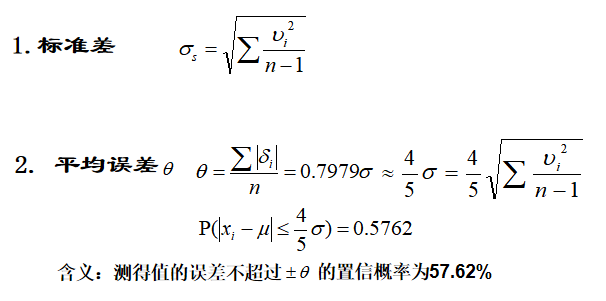

在一个测量列中,是以算术平均值作为测量结果:

因此必须研究算术平均值不可靠的评定标准!
第4节 多次测量结果的精度指标
算数平均值的分布特性与标准差
用 x ‾ \overline{x} x 作为测量结果比用单次测量结果精度提高了 n \sqrt{n} n倍!


算数平均值的置信度
测量次数多时,查正态分布表
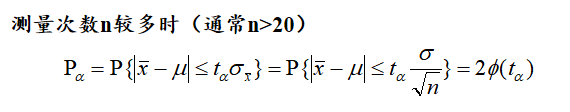

测量次数n较少时——t分布求解

当自由度趋向于无穷大时,t分布就是标准的正态分布。实际上在测量次数足够大(n>20),可以近似用正态分布代替。

其中自由度V=n-1=4,a=0.05。
t分布在数理统计中称为小子样分布。在精密测量中,测量次数很少有超过20次的,因此,在理论上应按t分布来计算相应的误差限;只有在测量次数较多(n>20)的情况时,或其测量量不甚重要时,才可近似应用正态分布的理论来处理。
事实上,当n无限增大时,t分布曲线和正态分布曲线基本重合,即按两个分布理论来处理测量数据,所得的结果差异是极小的。
算数平均值的精度指标(常用的有4个)

第5节 非等精度测量
什么是非等精度测量
测量条件(人员、方法、测量次数、环境条件等)部分或者全部改变,导致测量的精度和可信赖程度不一样。这种测量称为非等精度测量。
客观上,由于条件限制,所有的测量都是非等精度测量。但是条件差别不大的测量,一般都当成等精度处理。
等精度测量特点:具有同一标准差 σ \sigma σ。
非等精度测量的两种情况
(1)用不同的测量次数进行对比测量
(2)用不同精度的仪器进行对比测量:互比核对目的。
“权”的概念和加权平均
权与方差的关系
方差越大,测量结果越不可靠,权应该越小。
权与方差成反比!权表示相对可靠程度,是一个无量纲的数,允许给各组的权数同时增大或者减小若干倍,而比例关系不变。
