2022最新版-李宏毅机器学习深度学习课程-P13 局部最小值与鞍点

 一、优化失败的原因

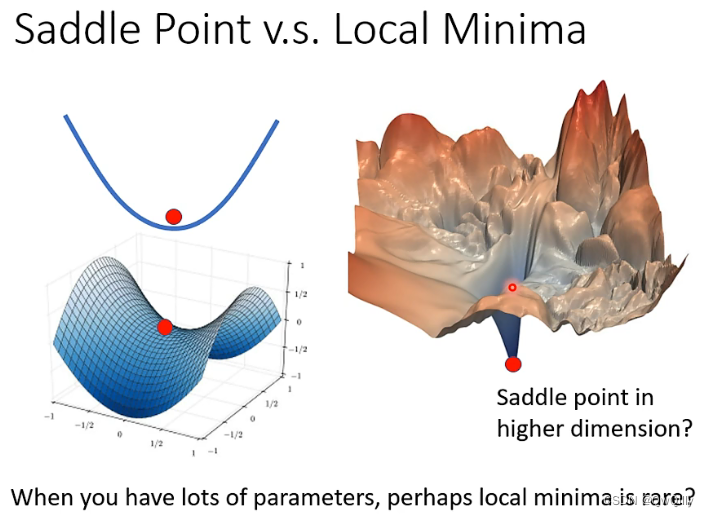
局部最小值？鞍点？

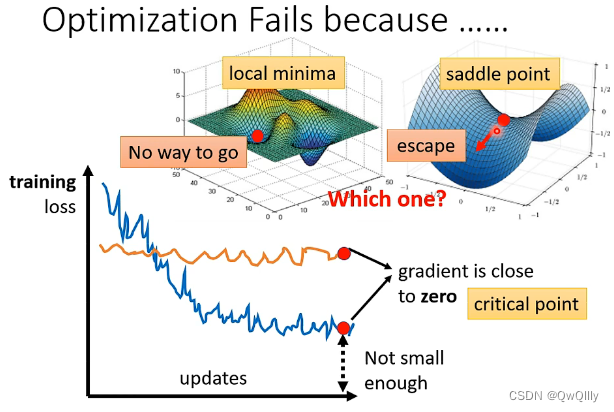
二、数学推导分析

用泰勒公式展开

一项与梯度（L的一阶导）有关，一项与海赛矩阵（L的二阶导）有关

海瑟矩阵

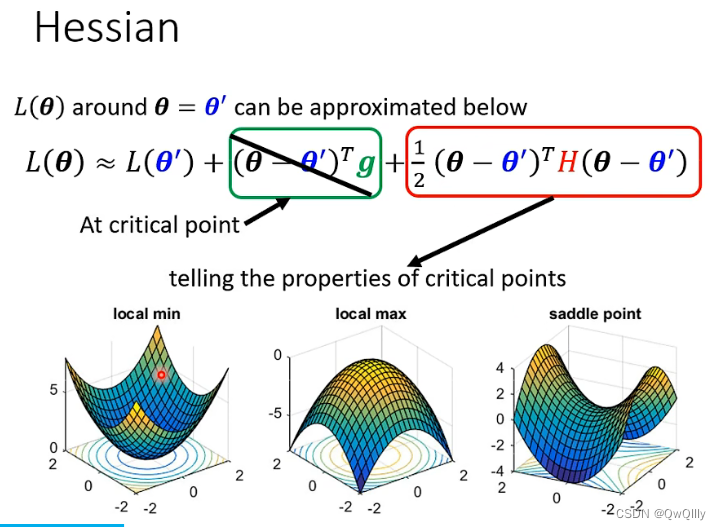
VTHV通过海瑟矩阵的性质可以转为判断H是否是正定的 来判断

• H正定=所有特征值为正=局部最小值
• H负定=所有特征值为负=局部最大值
• 有些特征值为正，有些为负=鞍点

例子

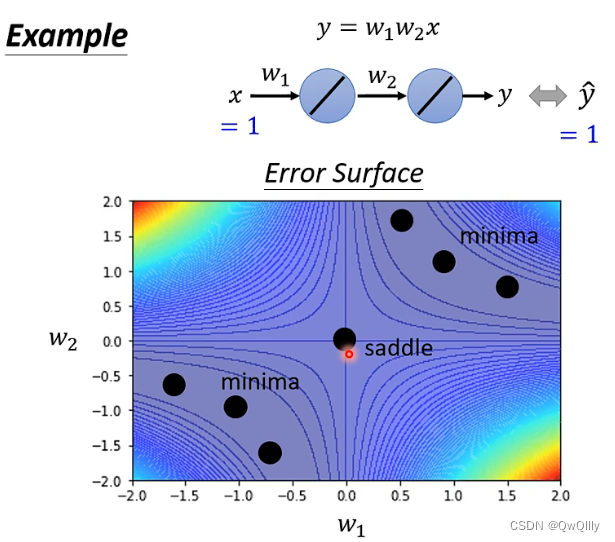
计算导数和海瑟矩阵的特征值

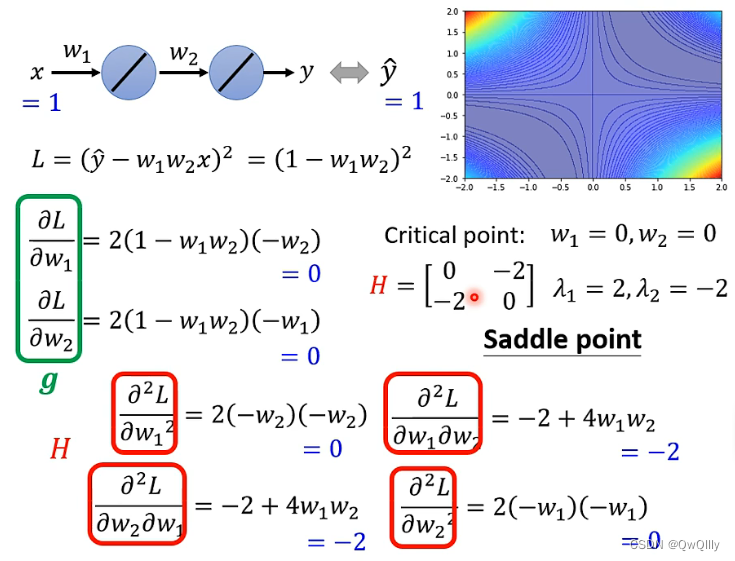
如果遇到鞍点，可以通过特征值来判断减小LOSS的方向：特征值为负的方向

其实局部最小值很少见，一升维，可能你碰上的就是个鞍点！

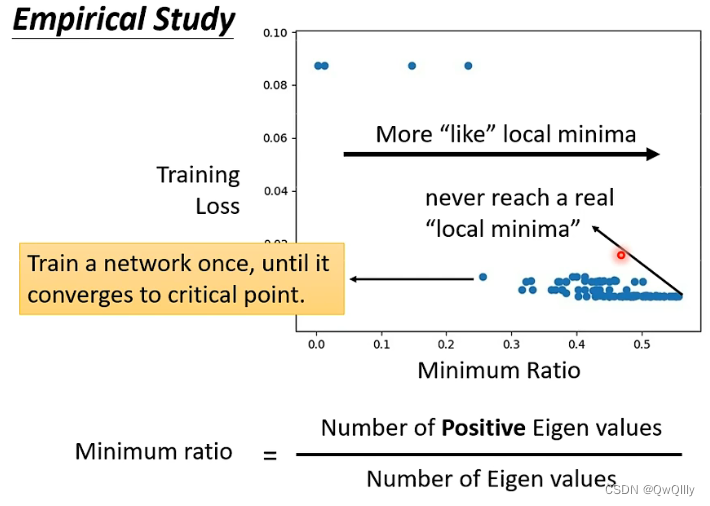
实验验证

注意这个方法肯定不是梯度下降法做的，做不出来，自己本身儿还一堆毛病呢。

纵轴：损失大小

横轴：局部最小值的比例=负特征值/全部特征值

解决梯度太小被困住的问题。。。下一小节：动量！