有限差分法求解不可压NS方程
网上关于有限差分法解NS方程的程序实现不尽完备,这里是一些补充注解
现有的优秀资料
理论向
【1】如何从物理意义上理解NS方程? - 知乎
【2】NS方程数值解法:投影法的简单应用 - 知乎
【3】[计算流体力学] NS 方程的速度压力法差分格式_「已注销」的博客-CSDN博客
【4】有限差分法(Finite Difference Method)解方程:边界和内部结点的控制方程 - 简书
编程向
【5】【游戏流体力学基础及Unity代码(五)】用欧拉方程模拟无粘性染料之代码实现 - 知乎
【6】(CFD)投影法求解二维不可压缩N-S方程_陈天文的博客-CSDN博客_二维ns方程公式
【7】CFD101: 2D Lid Driven Cavity Flow - File Exchange - MATLAB Central
有限差分法求解流程按照【2】,网格离散方法按照【7】,压力泊松方程迭代按照【5】。
注1:速度定义在网格线上,压力定义在网格中心。对于整个流体域,为了编程方便起见,在四周多加一层网格(虚拟网格)。但并不是所有虚拟网格上都定义了速度,见下图
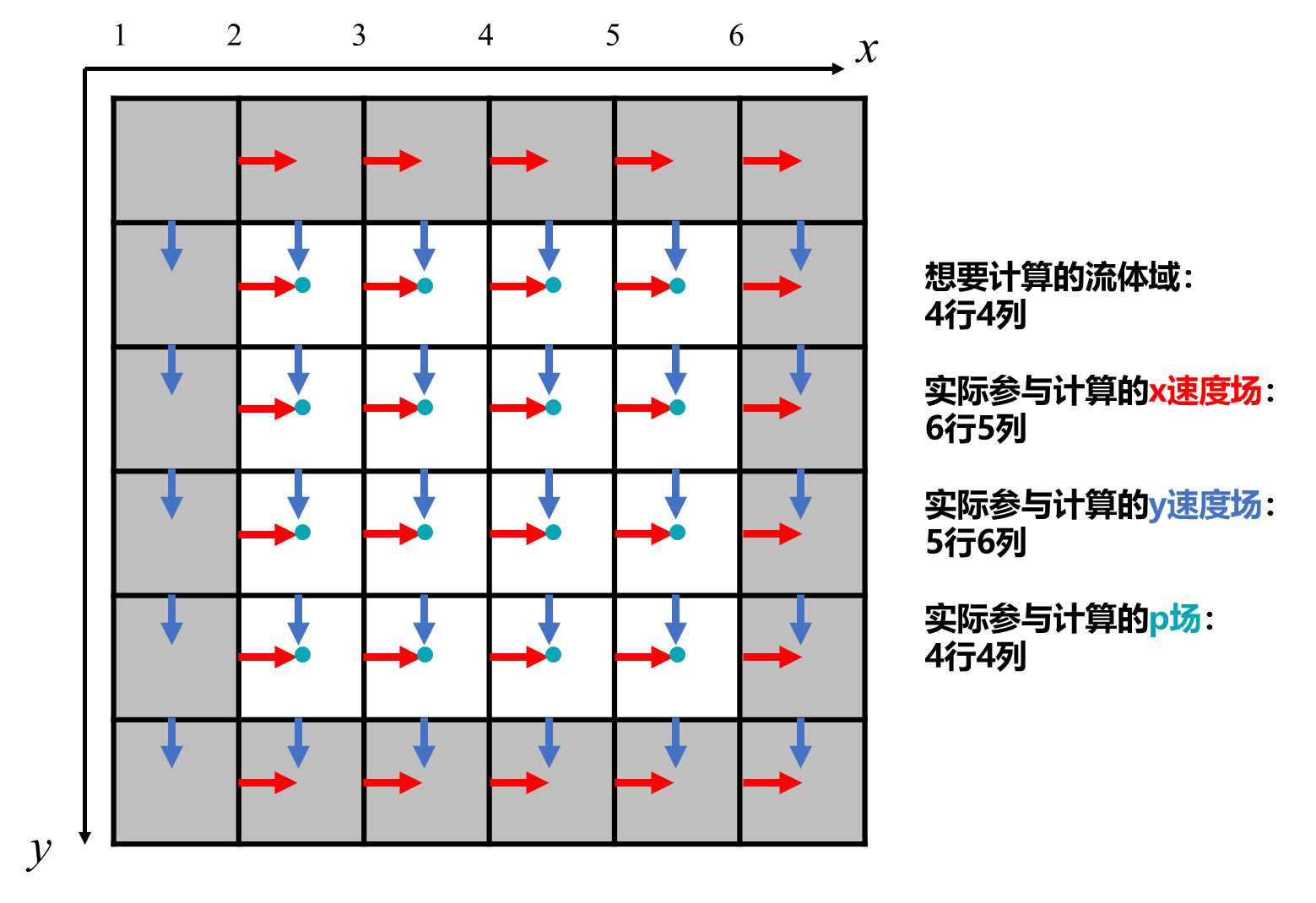
x方向速度定义在网格左边缘,而我们计算中不会用到左侧虚拟网格的速度,所以不需要定义第1列(x=1)的x方向速度。而对y方向速度,用第1列(x=1/2)y方向速度的原因是要算x=2处的y方向速度(x=1/2与x=3/2做平均)。
注2:方腔顶盖流似乎是某种标准的仿真验证工况,但是如果只验证这一种可能会发现不了一些问题。例如上面的【6】,无法计算左侧边界流入的情形,因为(对流项的)后向差分方法没法将左侧边界纳入计算。
对流项使用【7】中的散度形式似乎能解决这个问题,它使用了更多的平均,因此可以把周边的节点都考虑进来。
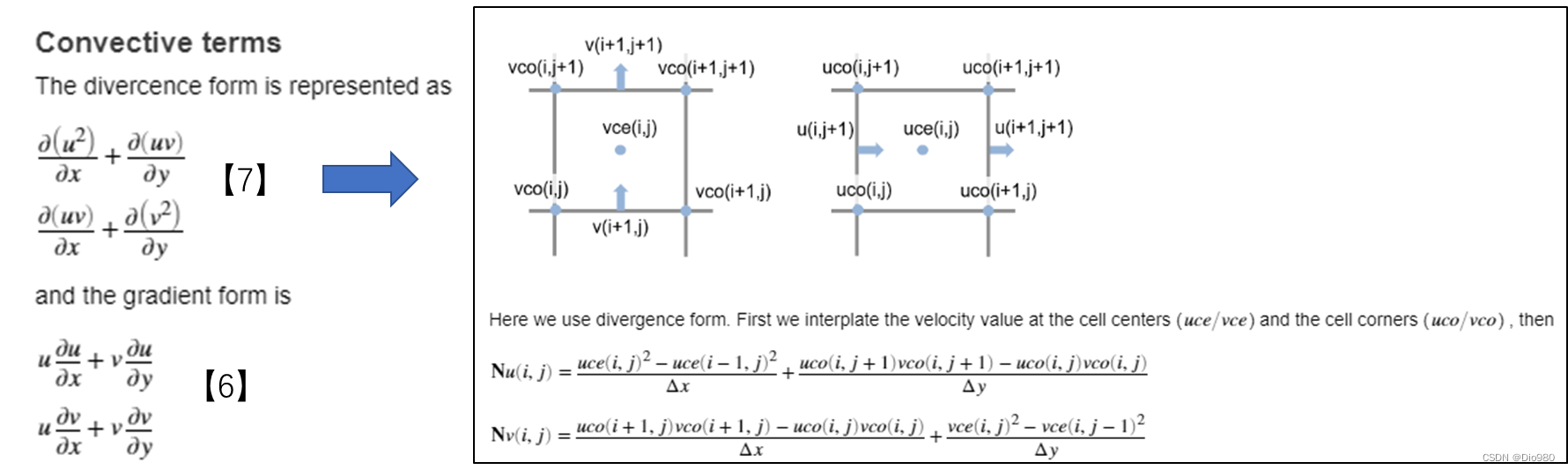
注3:方腔顶盖流只涉及了压力梯度为0和速度为0的边界条件。在每次压力迭代和速度迭代之前更新边界条件。对于边界法向的流动入口和出口,实测压力梯度为0可以保留,入口边界直接定义速度,出口边界速度梯度为0。但是还不清楚对于压力入口和滞止出口如何定义。
