正交实验与极差分析
正交试验极差分析流程如下图:

- 正交试验说明
正交试验是研究多因素试验的设计方法。对于多因素、多水平的实验要求,如果每个因素的每个水平都要进行试验,这样就会耗费大量的人力和时间,正交试验可以选择出具有代表性的少数试验进行试验,从而找出最优试验方案。
例如进行一个三因素三水平的试验,按照全面试验的思想,就要进行=27次实验,实验次数多且重复;但是如果选择进行正交试验就只需要做9次试验,大大节省了人力物力和时间,因此正交试验在很多领域都被广泛应用。 - 正交表设计
正交试验是通过现成的规格化表——正交表,科学的安排试验并通过极差分析或者方差分析来分析试验结果,找到最优试验方案的。
正交表是正交试验的基本工具,以正交表为例说明下正交表的概念和特点。式中L表示正交表,数字 3 表示因素的水平个数,右上指数为 4,标明最多可安排因素(包括交互)的个数。L右下的 9 表示本正交试验总的试验次数。即如采用该试验,那么可以完成安排最多4 个因素,每个因素最多 3个水平的总共9次的试验。
当前有一份三因素三水平的数据需要进行正交试验,目的是得到最优试验组合。
首先进行正交表的设计。设计正交表,可以使用SPSSAU进行,分析路径【SPSSAU->实验/医学研究->正交试验】。有时候可能会遇到SPSSAU输出的正交表的因素或水平数与预期不一致,是因为SPSSAU系统默认找到最接近的标准正交表,如果不一致,需要进行正交表的改造,例如使用拟水平法、组合法、并列法等。
具体操作可以查看SPSSAU帮助手册进行了解学习。https://spssau.com/helps/medicalmethod/orthogonal.html
本案例使用SPSSAU得到三因素三水平正交设计表如下:

得到正交设计表后,接下来需要按照正交表进行试验。
三、进行试验
从得到正交表可以看出,本次试验共需要进行9次。试验1为使用因子1的1水平、因子2的1水平和因子3的1水平进行试验;试验2为使用因子1的1水平、因子2的2水平和因子3的3水平进行试验,以此类推,分别得到9次试验的分析结果。
本次试验的三个因子分别是A、B、C,三个因子各有三个水平简单记为水平123,得到最终试验结果如下:
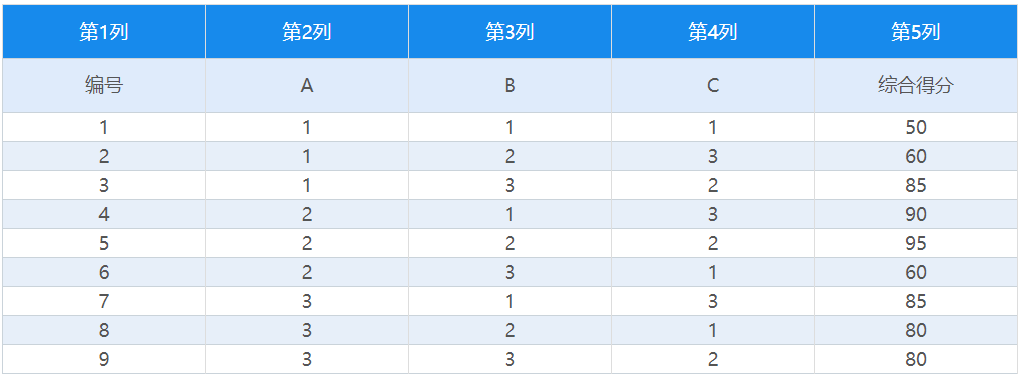
得到试验结果之后,对实验数据进行分析,目的是找到试验的最优因素和最优试验组合,即希望找到ABC三个因子中哪一个对综合得分的影响最优,同时找到综合得分最高的因素水平组合。
四、极差分析
对正交试验数据进行分析主要有两种分析方法,分别是极差分析与方差分析。极差分析又称直观分析法,它具有计算简单、直观形象、简单易懂等优点,是正交试验结果分析最常用的方法。本案例使用极差分析法进行分析。
极差分析设计的相关指标机器说明,如下表所示:

使用SPSSAU进行极差分析,操作如下图,需要注意的是,SPSSAU默认情况下试验数据越大越好,如果试验数据越小越好,此时可下拉选择‘试验数据类型’参数为‘越小越好’即可。

极差分析输出两类结果,分别是极差分析表格和因子各水平均值图。接下来进行极差分析结果解读,确定最优因素和最佳因素水平组合。
五、结果解读
结果1:极差分析表格

首先看R值(因素极差值):R值的大小反映了各因素对于试验结果的影响程度大小。所以本次试验结果显示,C因素为最优因素,对试验结果影响最大,其次是A因素,最后是B因素。因而三个因素的优劣排列顺序为因子C>因子A>因子B。
再看最佳水平:最佳水平显示,因子A在水平3的时候最优;因子B在水平2的时候最优;因子3在水平2的时候最优。
综合上述分析,得到这次试验的最优因素是“因子C”,最佳因素水平组合是“因子A的3水平、因子B的2水平、因子C的2水平”。
结果2:因子各水平均值图
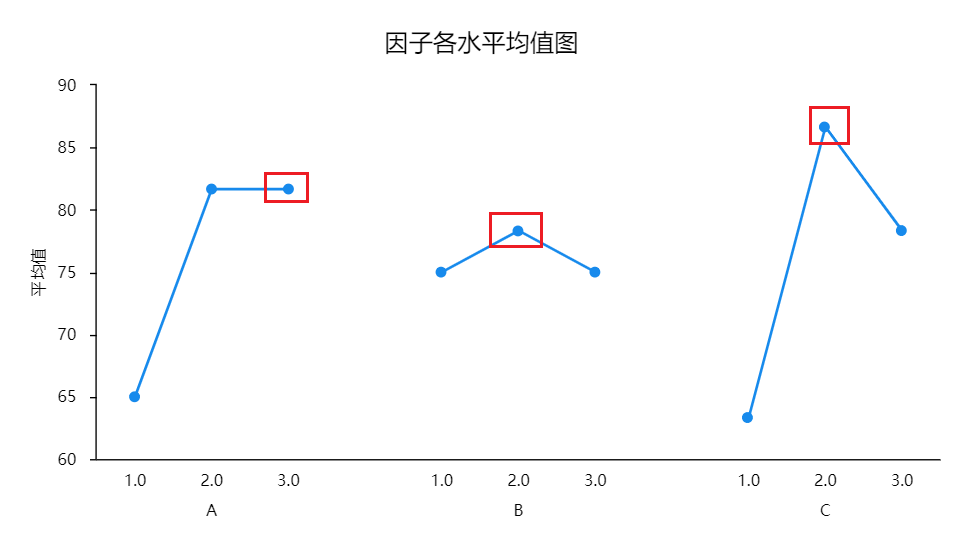
因素各水平均值图展示各个因素各个水平的试验数据平均值情况;可通过图形直观查看各水平的试验数据平均值情况并进行对比;并找出最佳水平组合,进行分析汇总。从上图也可以直观看出最佳因素水平组合为“因子A的3水平、因子B的2水平、因子C的2水平”。
六、总结
进行正交试验分析,首先需要进行正交表的设计, SPSSAU默认找到最接近的标准正交表,如果与试验预期不符,可以进行正交表的改造后再使用。然后根据得到的正交表进行试验,记录好试验结果,上传到SPSSAU系统。最后使用极差分析(或方差分析)来分析正交试验结果,得到最优因素和最佳因素水平组合。
