代码随想录算法训练营第三十九天 | 62.不同路径,63. 不同路径 II
一、参考资料
不同路径
https://programmercarl.com/0062.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE%84.html
视频讲解:https://www.bilibili.com/video/BV1ve4y1x7Eu
不同路径 II
https://programmercarl.com/0063.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE%84II.htmlhttps://programmercarl.com/0063.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE%84II.html
视频讲解:https://www.bilibili.com/video/BV1Ld4y1k7c6
二、LeetCode62.不同路径
https://leetcode.cn/problems/unique-paths/description/
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7 输出:28
示例 2:
输入:m = 3, n = 2 输出:3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3 输出:28
示例 4:
输入:m = 3, n = 3 输出:6
提示:
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9

class Solution {
public:int uniquePaths(int m, int n) {if (n <= 1) return 1;vector<vector<int>> dp(m + 1, vector<int>(n + 1));for (int i = 1; i <= m; i++) dp[i][1] = 1;for (int j = 1; j <= n; j++) dp[1][j] = 1;for (int i = 2; i <= m; i++) {for (int j = 2; j <= n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m][n];}
};class Solution {
public:// 下标从0开始int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m; i++) dp[i][0] = 1;for (int j = 0; j < n; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};进一步优化:
class Solution {
public:int uniquePaths(int m, int n) {vector<int> dp(n);for (int i = 0; i < n; i++) dp[i] = 1;for (int j = 1; j < m; j++) {for (int i = 1; i < n; i++) {dp[i] += dp[i - 1];}}return dp[n - 1];}
};三、LeetCode63. 不同路径 II
https://leetcode.cn/problems/unique-paths-ii/description/
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:
输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
示例 2:
输入:obstacleGrid = [[0,1],[0,0]] 输出:1
提示:
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1
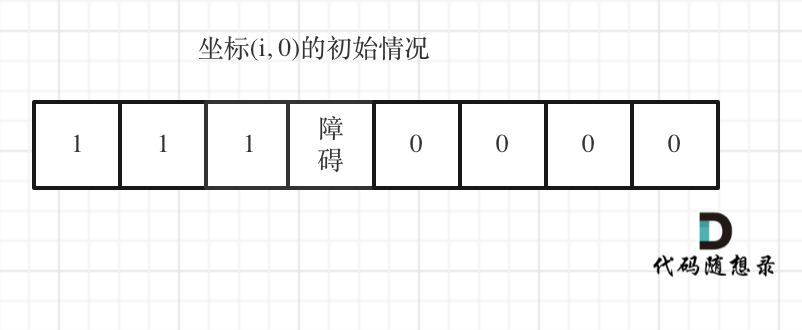
//dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) return 0;vector<vector<int>> dp(m, vector<int>(n));for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};空间优化版本:
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {if (obstacleGrid[0][0] == 1)return 0;vector<int> dp(obstacleGrid[0].size());for (int j = 0; j < dp.size(); ++j)if (obstacleGrid[0][j] == 1)dp[j] = 0;else if (j == 0)dp[j] = 1;elsedp[j] = dp[j-1];for (int i = 1; i < obstacleGrid.size(); ++i)for (int j = 0; j < dp.size(); ++j){if (obstacleGrid[i][j] == 1)dp[j] = 0;else if (j != 0)dp[j] = dp[j] + dp[j-1];}return dp.back();}
};