【算法小课堂】二分查找算法

简单思路:
当我们要从一个序列中查找一个元素的时候,最快想到的方法就是顺序查找法(即:从前到后依次查找)。但这种方法过于无脑,就是暴力的把每个元素都排查一遍。元素个数少的时候还行,一旦元素个数多起来,效率是非常低下,所以在实际中这种查找的方法是被摒弃的。
当题目或者实际对时间复杂度有着很高的要求的时候,这种暴力解法就显得很乏力
这里就不得不介绍一种简单且效率较高的查找方法了:二分查找法,又称折半查找法。但该方法是建立在有序的前提下的,基本思路就是:
利用两个指针left和right,不断取中点来不断把区间减小从而找到我们的答案
二分查找法的优势:
-
二分查找法的时间复杂度:O(logN)
-
暴力解法的时间复杂度:O(N)
如何直观来体现二分查找法时间复杂度的优势呢?
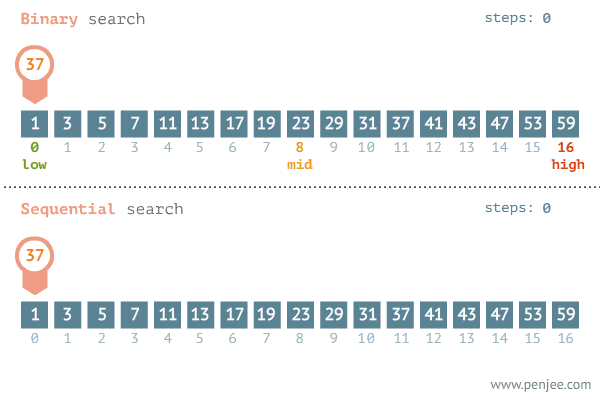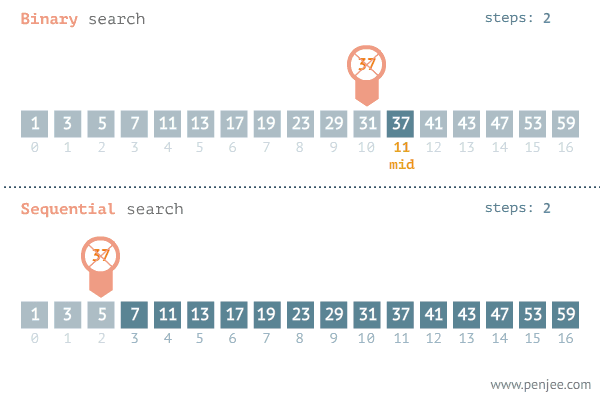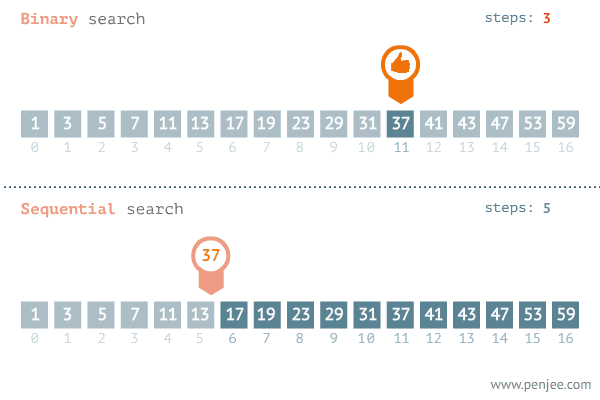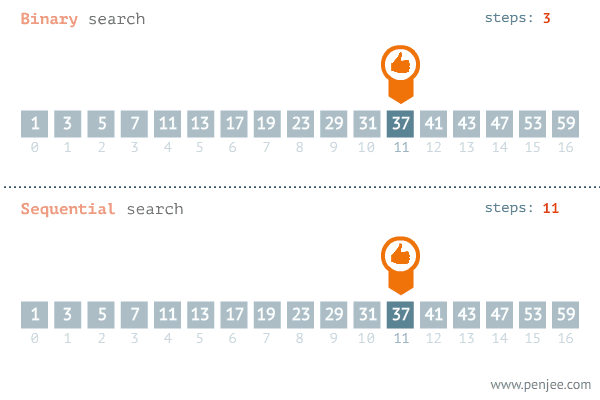
可以看出 二分查找 在查找数字 37 时只需3次,而 顺序查找 在查找37时需要12次。
二分查找的条件:
很多算法书都是写的具有有序性,其实更准确的是具有二段性
- 也就是具有可以把数组分为两端的性质
二分查找有两个限制条件:
- 查找的数量只能是一个,不能是多个
- 查找的对象在逻辑上必须是有序的(这个不是必要条件,更深层次是就有二段性)
朴素二分查找:
1.left=0,right=数组最后一个位置的下标
2.取中点:mid=(right-left)/2
二分法的思想很简单,因为整个数组是有序的,数组默认是递增的。
首先选择数组中间的数字和需要查找的目标值比较
-
如果相等最好,就可以直接返回答案了
-
如果不相等
如果中间的数字大于目标值,则中间数字向右的所有数字都大于目标值,全部排除
如果中间的数字小于目标值,则中间数字向左的所有数字都小于目标值,全部排除
704. 二分查找
以此题为例:
class Solution {
public:int search(vector<int>& nums, int target) {int left=0;int right=nums.size()-1;while(left<=right){int mid=left+(right-left)/2;if(nums[mid]==target) return mid;if(nums[mid]>target) right=mid-1;if(nums[mid]<target) left=mid+1;}return -1;}
};
朴素二分查找的模版:
while(left<=right){int mid=left+(right-left)/2;if(nums[mid]==target) return mid;if(nums[mid]>target) ...;if(nums[mid]<target) ...;}return ...;
二分查找左右端点:
我们通过一个例子:
34. 在排序数组中查找元素的第一个和最后一个位置
本题我们利用二分来解决左右端点的问题,首先left和right肯定有的
我们通过一个示例来了解本题:[1,2,3,3,3,4,5]
查找左端点:我们这里用t来代替target(这样比较好叙述)

- 二分的思路操作:我们可以将上述示例分为两个部分,因为我们现在查找左端点,因此我可以将示例分为【[1,2],[3,3,3,4,5]】

- 当x<t时,处于【1,2】这个区间,left=mid+1
- 当x>=t时,处于【3,3,3,4,5】这个区间,right=mid(这里不能等于mid-1,因为如果mid=0,right=-1会越界)
- 细节处理:
循环条件:
- left<right √
- left<=right ×
我们选择那种呢?我们来讨论一下:

- 有结果
- 全大于t(t1),right一直向左走,最后right为left结束,如果是left<=right会死循环
- 全小于t(t2),left一直向右走,最后left在right右边结束
以此我们只能选择第一种不能选择第二种!
求中间的操作:
- left+(right-left)/2 ×
- left+(right-left+1)/2 √
我们考虑一下极端情况就可以知道了!当只剩下两个元素的时候:

第一种没有问题,第二种mid=0+2/2=1,当进行left+1操作的时候会发生越界
查找右端点
- 二分的思路操作:我们可以将上述示例分为两个部分,因为我们现在查找左端点,因此我可以将示例分为【[1,2,3,3,3].[4,5]】

- 当x<=t时,处于【1,2,3,3,3】这个区间,left=mid
- 当x>t时,处于【4,5】这个区间,right=mid-1
- 细节处理:
循环条件:
- left<right √
- left<=right ×
还是选择left<right
求中间的操作:
- left+(right-left)/2 √
- left+(right-left+1)/2 ×
我们考虑一下极端情况就可以知道了!当只剩下两个元素的时候:
第一种当mid=0+1/2=0时,right=mid-1越界,第二种没有问题
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {//特殊情况处理一下if(nums.size()==0)return {-1,-1};int left=0,right=nums.size()-1;vector<int> ret;//查找左端点while(left<right){int mid=left+(right-left)/2;if(nums[mid]<target)left=mid+1;if(nums[mid]>=target)right=mid;}//当left==right时就是结果if(nums[left]!=target)return {-1,-1};else ret.push_back(left);//查找右端点left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left+1)/2;if(nums[mid]<=target)left=mid;if(nums[mid]>target)right=mid-1;}if(nums[right]!=target)return {-1,-1};else ret.push_back(right);return ret;}
};
查找区间左右端点的模版:

模版,这里主要是取中间这里不太一样,左端点时不用+1,右端点+1(记忆当下面出现-1,上面就+1)
至于left和right可以现场推导

