最短路径专题6 最短路径-多路径
题目: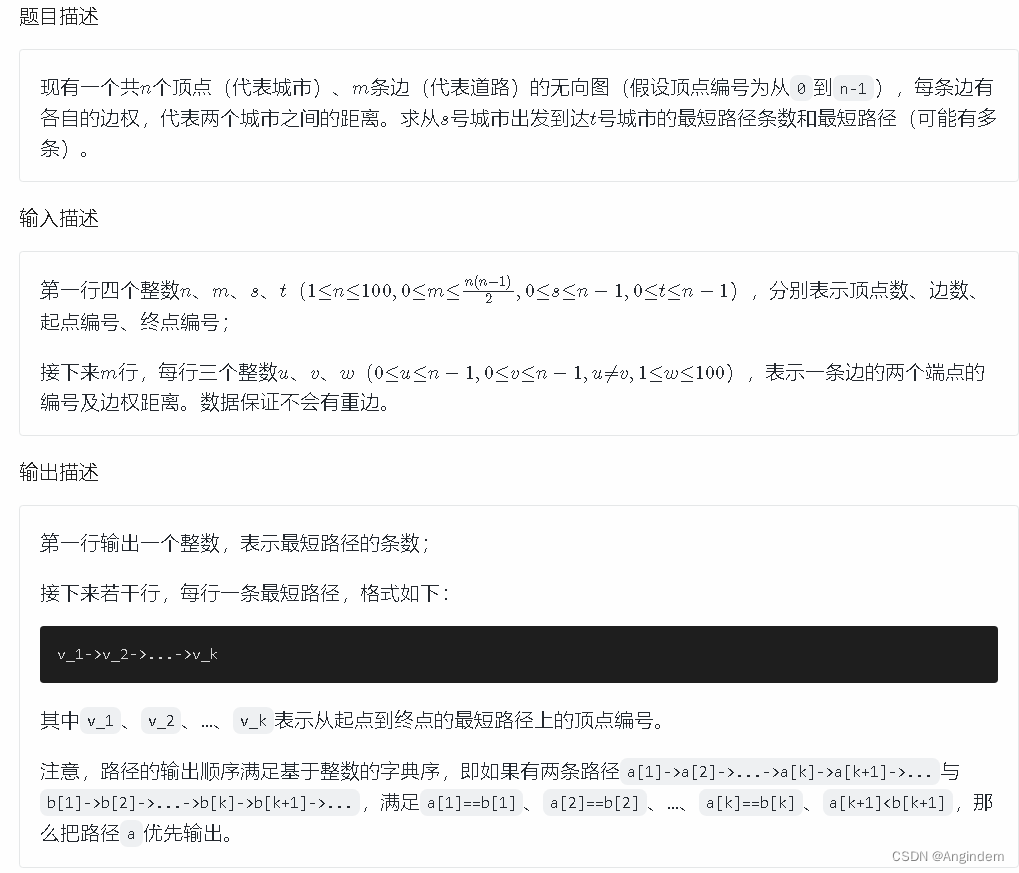
样例:
|
|
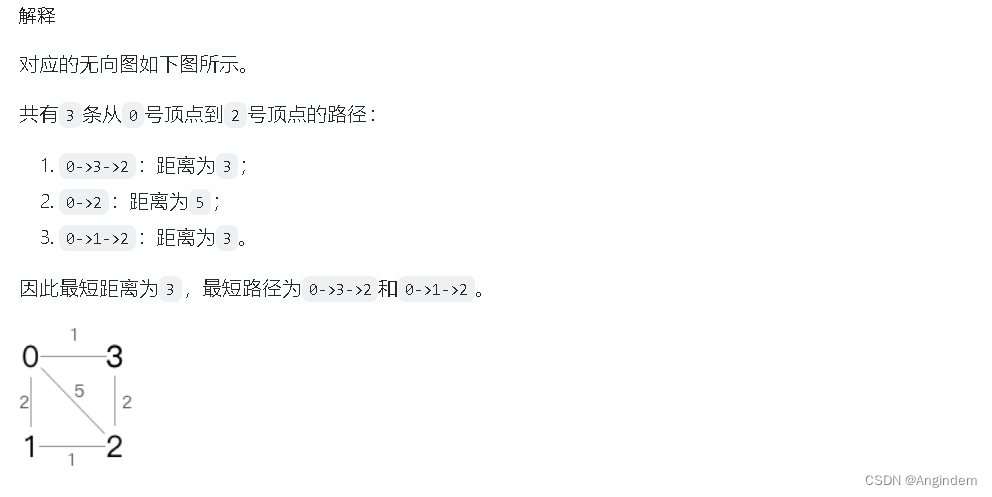
思路:
根据题意,最短路模板还是少不了的,
我们要添加的是,
记录各个结点有多少个上一个结点走动得来的,由于更新了最短路径,需要清空之前的记录的结点,重新记录当前结点由哪上一个结点得来的;
当遇到相同的最短路距离的时候,直接添加 j 结点也由 当前结点得来的。
最后递归遍历各个结点路径,并存储好,输出即可。
代码详解如下:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <unordered_map>
#define endl '\n'
#define x first
#define y second
#define mk make_pair
#define int long long
#define NO puts("NO")
#define YES puts("YES")
#define umap unordered_map
#define INF 0x3f3f3f3f3f3f3f3f
#define All(x) (x).begin(),(x).end()
#pragma GCC optimize(3,"Ofast","inline")
#define ___G std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;
using PII = pair<int,int>;int n,k,start,last;int dist[N];
bool st[N];// 建立链表
int h[N],e[N],w[N],ne[N],idx;
inline void Add(int a,int b,int c)
{e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx++;
}vector<int>tree[N]; // 记录每个结点拥有哪些结点得来的inline void Dijkstra()
{memset(dist,INF,sizeof dist);dist[start] = 0;priority_queue<PII,vector<PII>,greater<PII>>q;q.push(mk(0,start));while(q.size()){PII now = q.top();q.pop();int a = now.y;int dis = now.x;if(st[a]) continue;st[a] = true;for(int i = h[a];i != -1;i = ne[i]){int j = e[i];if(dist[j] > dis + w[i]){dist[j] = dis + w[i];tree[j].clear(); // 更新了最短路径,所以清空上一个结点记录过的多个结点 路径tree[j].emplace_back(a); // j 结点记录 添加 a 结点得来的路径}else // 如果遇到相同最短路距离,j 结点 添加 当前的 a 结点路径if(dist[j] == dis + w[i]) tree[j].emplace_back(a);// 记录该结点,方便下一次的走动q.push(mk(dist[j],j));}}return ;
}vector<vector<int>>paths; // 记录多个路径
vector<int>tempPath; // 临时路径void getPath(int now)
{// 到达递归边界,开始回溯取各个路径if(now == start){tempPath.emplace_back(now); // 临时路径存储当前结点paths.emplace_back(tempPath); // 存储路径tempPath.pop_back(); // 弹出存储的当前结点,进行回溯,寻找另一条不同的路径return ;}tempPath.emplace_back(now); // 临时路径存储当前结点// 遍历 当前结点 now 由哪个结点得来的// 递归获取路径结点for(auto i : tree[now]){getPath(i);}tempPath.pop_back(); // 弹出存储的当前结点,进行回溯,寻找另一条不同的路径return ;
}inline void solve()
{// 初始化链表memset(h,-1,sizeof h);cin >> n >> k >> start >> last;while(k--){int a,b,c;cin >> a >> b >> c;Add(a,b,c);Add(b,a,c);}// 求最短路径Dijkstra();// 获取最短路径getPath(last);int sum = paths.size(); // 总的路径数量// 翻转获得的全部路径,由于我们是从终点往后获取的// 所以需要翻转一下for(int i = 0;i < sum;++i){reverse(All(paths[i]));}// 根据题意,字典序排序好每条路径sort(All(paths));// 输出路径条数cout << sum << endl;// 输出记录的每条最短路路径for(int i = 0;i < sum;++i){bool rem = false; // 控制格式for(int j : paths[i]){if(rem) cout << "->";cout << j;rem = true;}cout << endl;}
}
signed main()
{
// freopen("a.txt", "r", stdin);___G;int _t = 1;
// cin >> _t;while (_t--){solve();}return 0;
}
