当前位置：首页 > news >正文

【C语言】函数的定义、传参与调用（二）

news 2025/7/21 12:04:51

💗个人主页💗

⭐个人专栏——C语言初步学习⭐

💫点击关注🤩一起学习C语言💯💫

导读：

1. 函数的嵌套调用

1.1 什么是嵌套调用

1.2 基础实现

1.3 调用流程解析

2. 函数的链式访问

2.1 什么是链式访问

2.2 基础实现

3. 函数递归

3.1 什么是递归

3.2 递归的两个必要条件

3.3 用递归方法求n!

4. 小结练习

导读：

在前面，我们了解了第一部分的函数的定义、传参与调用（一），在这里我们基本了解了该怎样定义和使用一个函数。

现在我们来进一步的学习函数的嵌套和递归💯

1. 函数的嵌套调用

1.1 什么是嵌套调用

C语言的函数定义是互相平行、独立的，也就是说，在定义函数时，一个函数内不能在定义另一个函数，即不能嵌套定义，但可以嵌套调用函数。

函数的嵌套调用指在一个函数中调用另一个函数，而被调用的函数又可以是其他函数的参数或返回值。这种嵌套调用的方式可以让程序更加灵活和高效。

1.2 基础实现

在调用函数时，需要注意以下几点：

函数名必须与函数定义的名称一致，包括大小写。
调用函数时，必须传递该函数所需要的参数，参数的顺序和类型必须与函数定义时一致。
如果函数没有参数，则在调用函数时应该留空参数列表

例如：

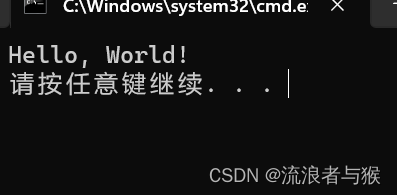
void B()
{printf("Hello, World!\n");
}
void A()
{B();
}
int main()
{A();return 0;
}

1.3 调用流程解析

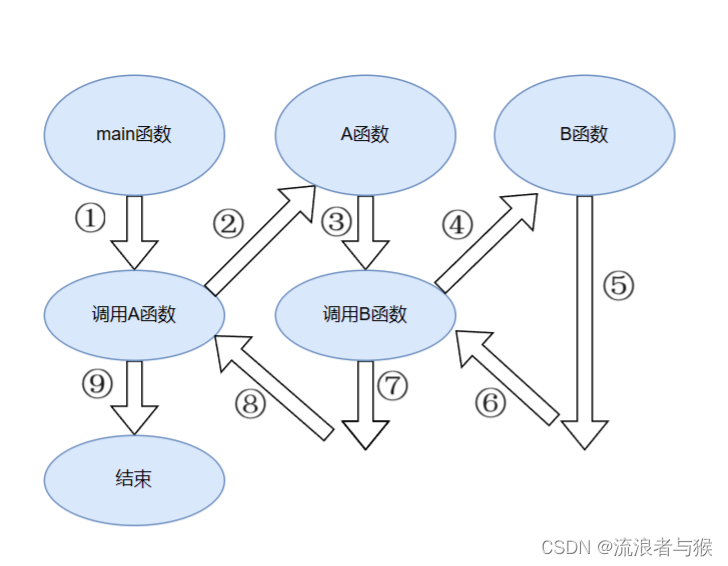
①执行main函数的开头部分

②遇函数调用语句，调用函数A，流程转去A函数

③执行A函数的开头部分

④遇函数调用语句，调用函数B，流程转去B函数

⑤执行B函数，如果再无其他嵌套的函数，则完成B函数的全部操作

⑥返回到A函数中调用B函数的位置

⑦继续执行A函数中尚未执行的部分，知道A函数结束

⑧返回main函数中调用a函数的位置

⑨继续执行main函数的剩余部分直到结束

2. 函数的链式访问

2.1 什么是链式访问

在C语言中，可以使用函数的链式访问来简化对多个函数的调用过程。

所谓链式访问，就是通过函数返回值的方式，实现对多个函数的连续调用。具体来说，就是将一个函数的返回值作为另一个函数的输入参数，从而实现多个函数的顺序调用。

2.2 基础实现

int add(int a, int b) 
{return a + b;
}
int multiply(int a, int b) 
{return a * b;
}
int main() 
{int x = 1;int y = 2;int z = 0;z = multiply(add(x, y), y);printf("(%d + %d) * %d = %d\n", x, y, y, z);return 0;
}

解析：

我们定义了两个函数add和multiply。

在main函数中，我们首先调用add函数，计算出x和y的和，然后将结果作为input传递给multiply函数，计算出input和y的乘积，最后将乘积的结果赋值给变量z。由于add函数返回值的类型和multiply函数的输入参数类型是一致的，所以我们可以直接将add函数的返回值作为multiply函数的输入参数，从而实现了链式访问。

3. 函数递归

3.1 什么是递归

程序调用自身的编程技巧称为递归（ recursion）

递归做为一种算法在程序设计语言中广泛应用。

一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。

递归的主要思考方式在于：把大事化小

3.2 递归的两个必要条件

存在限制条件，当满足这个限制条件的时候，递归便不再继续。
每次递归调用之后越来越接近这个限制条件。

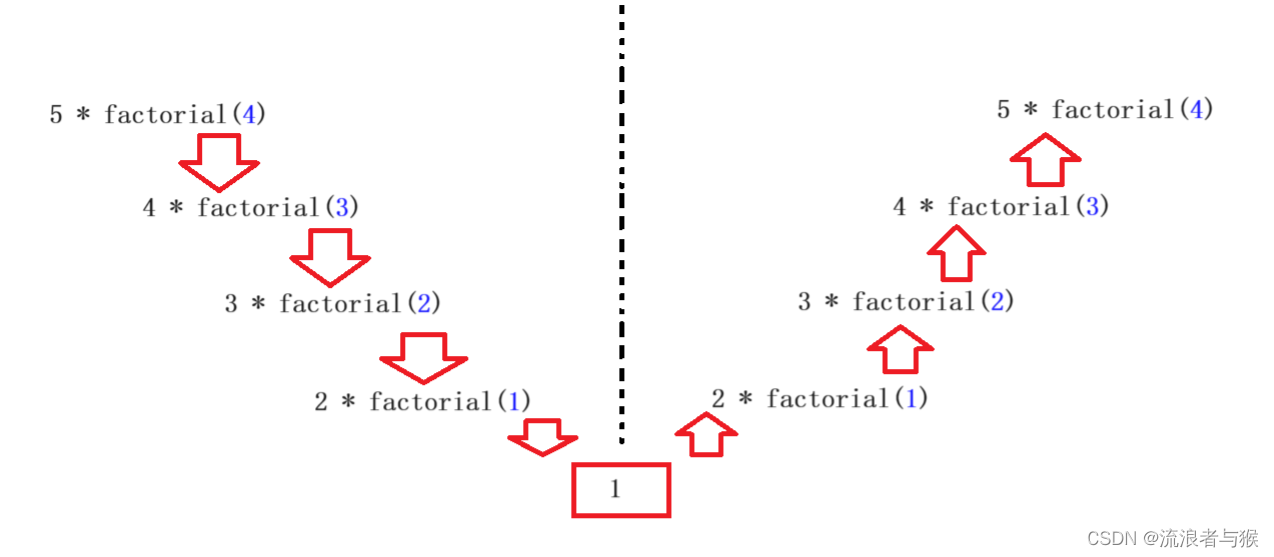
3.3 用递归方法求n!

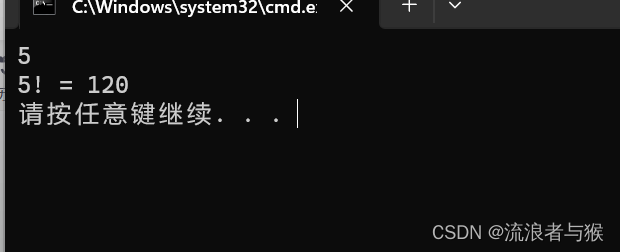
int factorial(int n) 
{if (n == 0 || n == 1) {return 1;  // n为0或1时，阶乘为1}else {return n * factorial(n - 1);  // 递归调用自身，计算n-1的阶乘}
}
int main() 
{int n = 0;scanf("%d", &n);int res = factorial(n);  // 计算n的阶乘printf("%d! = %d\n", n, res);return 0;
}